Решение.
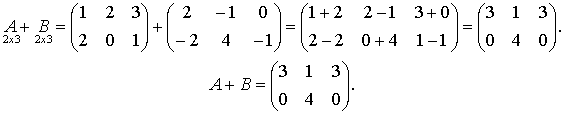
Рассмотрим еще один пример
Пример 2. Пусть даны матрицы:
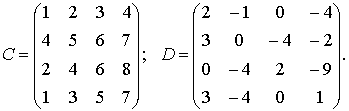
Решение.
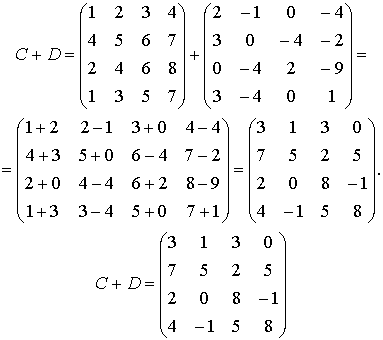
Вычитание матрицы = 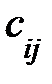
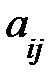 -
- 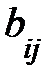
Умножение матрицы на число. Произведением матрицы Am´n×λ наз-ся число матрицы Bm´n=Am´n× λ= λ× Am´n элементы которой 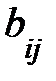 = λ*
= λ* 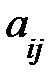 Общий множитель всех элементов матрицы можно выносить за знак этой матриц
Общий множитель всех элементов матрицы можно выносить за знак этой матриц
Например, пусть 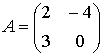
Найти результат умножения матрицы А на число 4.
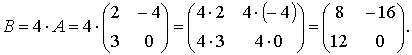
Умножение матрицы на матрицу. Произведением матрицы Аm´k на матрицу Bk´n называется матрица Cm´n каждый элемент которой 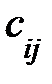 равен сумме произведений элементов і –ой (итой) строки матрицы А на соответствующие элементы j -го (житого) столбца матрицы В, т.е. Cij= ai1*b1j+ai2*b2j+…+aik*bkj ═ =
равен сумме произведений элементов і –ой (итой) строки матрицы А на соответствующие элементы j -го (житого) столбца матрицы В, т.е. Cij= ai1*b1j+ai2*b2j+…+aik*bkj ═ = 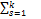 ais bsj
ais bsj
Замечание: Умножать можно только согласованные матрицы. Две матрицы А и В называются согласованными, если число столбцов в первой матрице А равно числу строк во второй матрице В
Пример.
А= 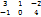 ; В=
; В= 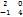
2´ 32 ´ 2
А×В – не сущ-ет, т.к м-цы А и В не согласованные(3×2)
В × А – согласованные
2´2 2´3
В×А = 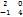 ×
× 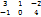 =
= 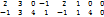
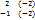
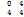 =
= 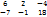
Квадратные матрицы одного порядка всегда согласованные
Транспонирование матрицы. Am´n матрица полученная из матрицы А, заменой её строк столбцами без изменения порядка их следования наз-ся транспонированной к матрице А и обозначается Ат
А= 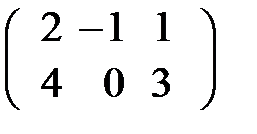 Ат=
Ат= 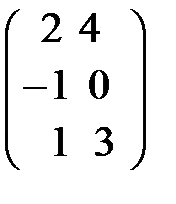
2 ´ 33 ´ 2
Замечание: Матрица А называется симметрично й, если А=А 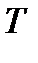 , и кососимметричной, если А = –А
, и кососимметричной, если А = –А 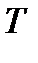 .
.
Возведение матрицы в степень (только для квадратных м-ц) А п =А*А*А*…*А
Вопрос 2. Определители 2-го и 3-го порядков. Свойства определителей.
Определитель - это число, определяемое по некоторой формуле
Определитель м-цы А обозначается det A или │ A │, и ли ∆. П онятие опред-ля имеет смысл только для квадр-х м-ц.
1. Опред-м м-цы А первого порядка А= [ aij ] наз-ся число aij │ A │= aij (А= │ 5 │,│ A │=5); (А= │ -3 │,│ A │=-3)
2. Опред-м м-цы второго порядка А = 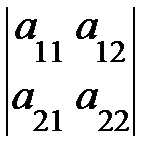 наз-ся число опред-ое по формуле
наз-ся число опред-ое по формуле 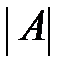 =
= 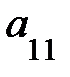
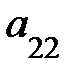 –
– 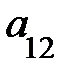
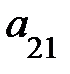
свойства:
1. Определитель не изменится при замене всех его строк соответствующими столбцами: 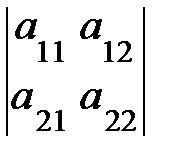 =
= 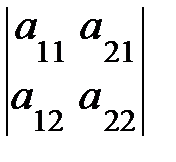 .
.
2. Знак определителя меняется на противоположный при перестановке строк (столбцов) определителя:
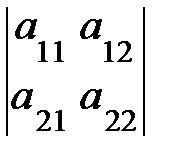 = –
= – 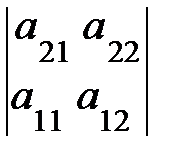 ,
, 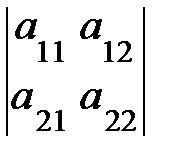 = –
= – 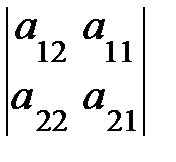 .
.
3. Общий множитель всех элементов строки (столбца) определителя можно вынести за знак определителя:
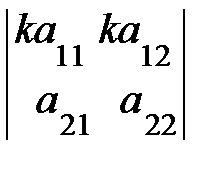 =
= 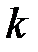
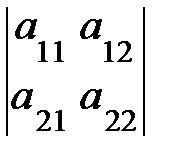 или
или 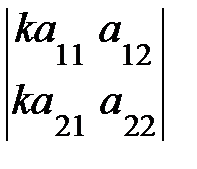 =
= 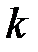
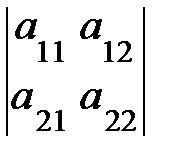 .
.
4. Если все элементы некоторой строки (столбца) определителя равны нулю, то определитель равен нулю.
5. Определитель равен нулю, если соответствующие элементы его строк (столбцов) пропорциональны:
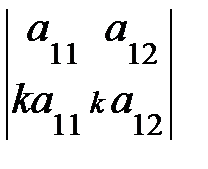 =0,
=0, 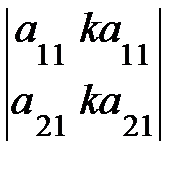 = 0.
= 0.
6. Если элементы одной строки (столбца) определителя равны сумме двух слагаемых, то такой определитель равен сумме двух определителей: 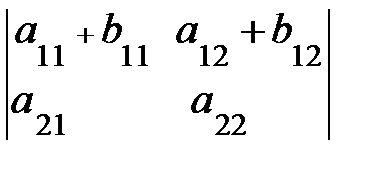 =
= 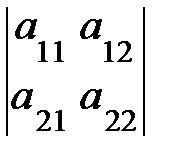 +
+ 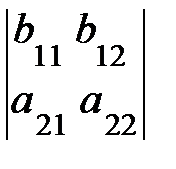 ,
, 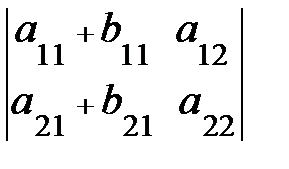 =
= 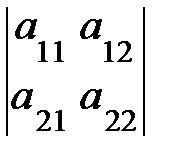 +
+ 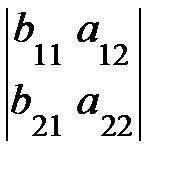 .
.
7. Значение определителя не изменится, если к элементам его строки (столбца) прибавить (вычесть) соответственные элементы другой строки (столбца), умноженные на одно и тоже число 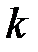 :
:
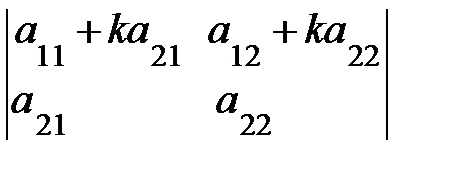 =
= 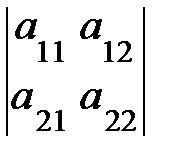 +
+ 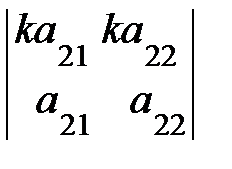 =
= 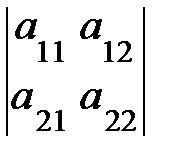 , так как
, так как 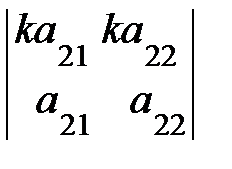 =0 по свойству 5.
=0 по свойству 5.
3. Опред-м м-цы третьего порядка наз. число кот-е вычисляется по формуле
Δ = 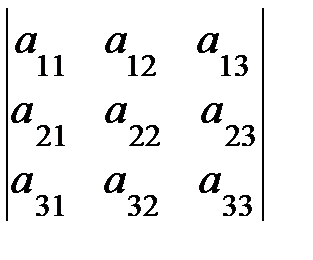 =
= 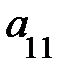
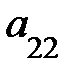
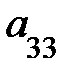 +
+ 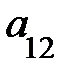
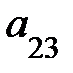
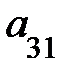 +
+ 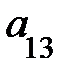
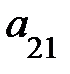
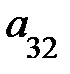 -
- 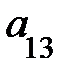
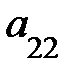
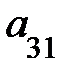 -
- 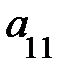
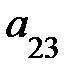
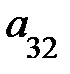 -
- 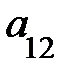
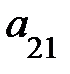
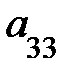 ,
,
Вопрос 3. Миноры и алгебраические дополнения. Вычисление определителей с помощью формул разложения.
Минором М ij элемента aij наз-ся опред-ль,м-цы (n-1)-го порядка полученный из м-цы А вычеркиванием итой строки и житого столбца,
Пример: А=│ 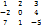 │;
│;
М 23=│ 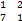 │=1*1 - 2*7=13; а 23=4.
│=1*1 - 2*7=13; а 23=4.
М 12=│ 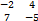 │= -2*(-5) - 4*7= -18; а 12 = 2.; М 22=│
│= -2*(-5) - 4*7= -18; а 12 = 2.; М 22=│ 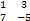 │= -5-21=26; а 22=0.
│= -5-21=26; а 22=0.
Алгебраическим дополнением элемента 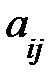 определителя
определителя 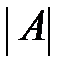 называется его минор
называется его минор 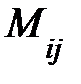 , взятый со знаком
, взятый со знаком 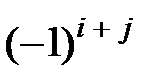 . Алгебраическое дополнение будем обозначать
. Алгебраическое дополнение будем обозначать 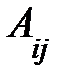 , то есть
, то есть 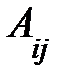 =
= 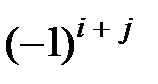 *
* 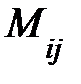 .
.
(8 св-во опред-ля)Теорема Лапласа. Определитель квадратной м-цы А п- го порядка равен сумме всех произведений элементов произвольной строки (столбца) на их алгебраические дополнения
Разложение по эл-там итой строки -│А│= аi1* А i1+ аi2* А i2+…+ аin* А in
Разложение по элементам житого столбца - │А│= а1j * А 1j + а2j* А2j +…+ аnj *Аnj
(9 св-во определителя) Теорема аннулирования: сумма всех произведений элементов одной строки (столбца) определителя на соответствующие алгебраические дополнения элементов другой строки (столбца) равна нулю, то есть 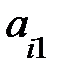
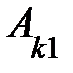 +
+ 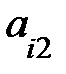
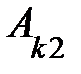 +
+ 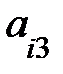
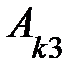 = 0,
= 0, 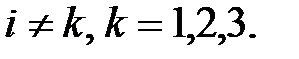
Опред-ль произведения двух квадратных м-ц равен произведению определителей этих квадратных матриц: 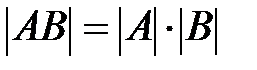
Вопрос 4. Обратная матрица и её вычисление.
Квадратная матрица А порядка n называется новорожденной (неособенной ), если её опред-ль не равен 0 ( det A ≠ 0);
в противном случае матрица наз-ся выражденной (особенной) (det A = 0)
Обратной м-цей для квадратной м-цы А порядка n наз-ся м-ца 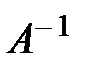 , если выполняются равенства
, если выполняются равенства 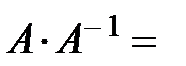
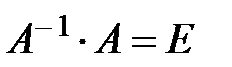 , где Е – единичная матрица того же порядка n, что и м-ца А
, где Е – единичная матрица того же порядка n, что и м-ца А
Теорема: Необходимое и достаточное условие существования м-цы. Для того, чтобы квадр-я м-ца А имела обратную, необходимо и достаточно, чтобы она была выражденной.
Алгоритм нахождения обратной матрицы:
1) Вычисляем опред-ль м-цы А. Если опред-ль м-цы А = 0, то обратной м-цы не сущ-ет. Если А≠0, то 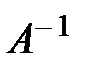 сущ-ет.
сущ-ет.
2) Строим м-цу 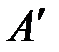 составленную из алгебраических дополнений к м-це А:
составленную из алгебраических дополнений к м-це А: 
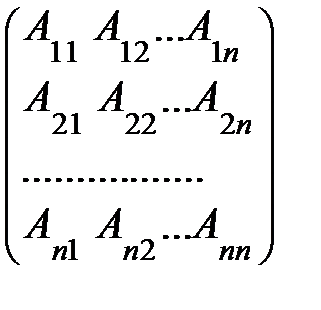 .
.
3) Строим присоединительную м-цу 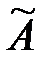 к м-це
к м-це 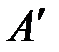 :
: 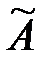 - (
- (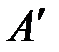 )т=
)т= 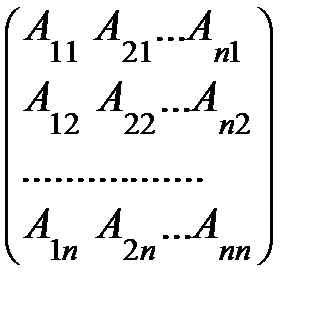 .
.
4) Находим обратную м-цу по формуле: 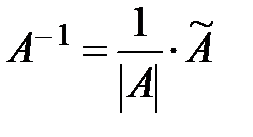
Необходимо сделать проверку:
А * 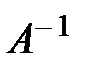 = Е
= Е
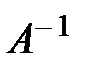 * А=Е
* А=Е
Св-ва обратной м-цы
1. 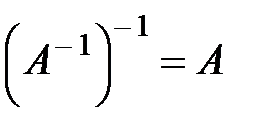 ;
;
2. 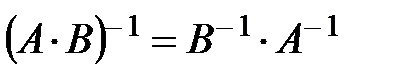 ;
;
3. 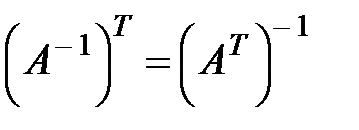 .
.
Вопрос 5. Ранг матрицы. Вычисление ранга с помощью элементарных преобразований.
Рангом r (A) м-цы А наз-ся макс-ый порядок ее миноров, отличных от нуля. Минором k-го(факториального) порядка м-цы А наз-ся опред-ль k-го(факториального) порядка, построенный из эл-тов м-цы А, находящихся на пересечении k строк и k столбцов м-цы А. Базисным минором м-цы наз-ся всякий отличный от нуля минор, порядок кот-го = рангу данной м-цы. Ранг м-цы = 0 тогда, когда А – нулевая м-ца.
Пример: Определить ранг матрицы А= 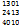
Решение: Матрица А имеет порядок 3×4, следовательно, ранг матрицы 0 ≤ r (A) ≤ 3. Для опред-ния ранга вначале найдем все возможные миноры 3-го порядка: если хотя бы один из них отличен от нуля, значит, ранг м-цы А равен трем. Всего имеем 4 минора 3-го порядка:  ,
,  ,
,  ,
, 
Т. к. достаточно найти среди них хотя бы один, отличный от нуля, то выберем тот минор, который содержит большее кол-во нулевых элементов:  = 1*(-1)3+2
= 1*(-1)3+2 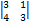 = -(9-4)= -5¹ 0 Þ r(A) = 3..
= -(9-4)= -5¹ 0 Þ r(A) = 3..
Данный минор будет являться базисным для исходной м-цы.Если бы все приведенные в примере миноры 3-го порядка оказались =-ми 0, то это привело бы к рассмотрению миноров 2-го порядка. В этом случае ранг м-цы был бы меньше трех. М-цы А и В наз-тся эквивалентными (А~В), если одна из них получается из другой с помощью элементарных преобразований.
К элементарным преобразованиям относят:
1) перестановку местами любых двух строк (столбцов) матрицы;
2) умножение каждого элемента строки (столбца) на один и тот же множитель λ ≠ 0;
3) прибавл-ие (выч-ие) к эл-там строки (столбца) соотв-щих эл-тов другой строки (столбца), умнож-х на один и тот же множитель.
Ранги эквивалентных м-ц совпадают, т.е. ранг м-цы не меняется, если к м-це применить элементарные преобразования 1-3. Если хотя бы один эл-нт м-цы А  0, то ранг м-цы больше нуля. Таким образом, ранг является еще одной важной характеристикой матрицы. Имеют место следующие утверждения:
0, то ранг м-цы больше нуля. Таким образом, ранг является еще одной важной характеристикой матрицы. Имеют место следующие утверждения:
1) если ранг м-цы А = k, то сущ-ет ровно k линейно-независимых строк (столбцов), от кот-х линейно зависят все остальные строки (столбцы), т. е. все остальные строки выражаются ч-з эти k линейно-независимых строк;
2) макс-е число линейно-независ-х строк м-цы совпадает с макс-ым числом линейно-независ-х столбцов и = рангу м-цы.
Вопрос 6.Системы линейных алгебраических уравнений(ЛАУ). Матричный способ решения систем ЛАУ.
Системой m линейных алгебраических уравнений с n неизвестными x1, x2,..., xn называется система вида:
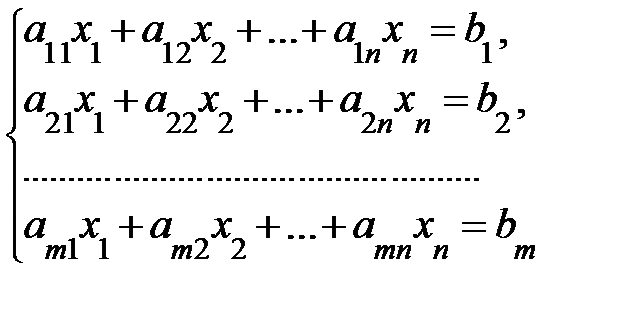 (1) Данная система может быть записана в матричном виде АХ = В, (2)
(1) Данная система может быть записана в матричном виде АХ = В, (2)
где А = 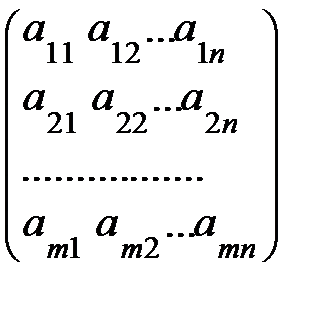 есть м-ца сис-мы (1), или м-ца коэф-тов;
есть м-ца сис-мы (1), или м-ца коэф-тов;
Х = 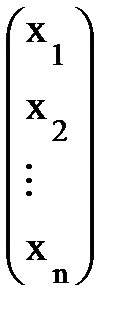 есть м-ца- столбец неизвестных; В =
есть м-ца- столбец неизвестных; В = 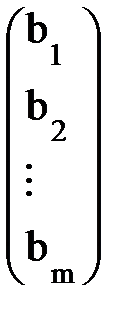 есть м-ца- столбец свободных членов.
есть м-ца- столбец свободных членов.
Если В = 0, то система (1) называется однородной, если же В ≠ 0, то неоднородной.
Решением сис-мы (1) наз. всякая совокупность чисел 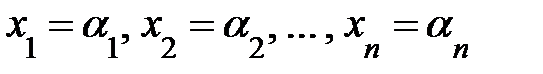 , кот-я, будучи подставленной в сис-му, превращает каждое ее урав-ние в тождество. Однако не каждая сис-ма ЛАУ имеет решение. Если не сущее-ет ни одной совокупности значений
, кот-я, будучи подставленной в сис-му, превращает каждое ее урав-ние в тождество. Однако не каждая сис-ма ЛАУ имеет решение. Если не сущее-ет ни одной совокупности значений 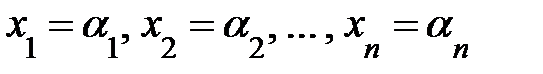 , удовлетворяющей заданным урав-ям сис-мы, то сис-ма (1) наз несовместной. В противном случае, сис-ма (1) наз совместной. Совместная сис-ма может иметь единственное реш-ие, или бесконечное множ-во реш-й.
, удовлетворяющей заданным урав-ям сис-мы, то сис-ма (1) наз несовместной. В противном случае, сис-ма (1) наз совместной. Совместная сис-ма может иметь единственное реш-ие, или бесконечное множ-во реш-й.
Матричный м-д решения систем ЛАУ. Если в сис-ме (1) m=n и det A ≠ 0 (м-ца невырожденная), то для неё сущ-ет обратная м-ца 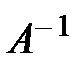 . Умножим обе части равенства (2) слева на
. Умножим обе части равенства (2) слева на 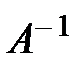 :
: 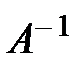 × А×Х =
× А×Х = 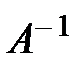 × В
× В 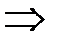 Е×Х =
Е×Х = 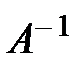 × В, отсюда Х =
× В, отсюда Х = 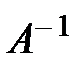 × В. (3) Формула (3) явл-ся матричной записью реш-я сис-мы ЛАУ. Т. к. обратная м-ца
× В. (3) Формула (3) явл-ся матричной записью реш-я сис-мы ЛАУ. Т. к. обратная м-ца 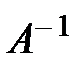 единственная, то сис-ма (1) имеет единственное реш-е. Таким образом для реш-я сис-мы ЛАУ матрич-м м-дом необх-мо найти обратную м-цу к м-це А и умножить её слева на столбец свободных членов В
единственная, то сис-ма (1) имеет единственное реш-е. Таким образом для реш-я сис-мы ЛАУ матрич-м м-дом необх-мо найти обратную м-цу к м-це А и умножить её слева на столбец свободных членов В
Правило Крамера: Если м-ца А сис-мы ЛАУ не выражденная, то сис-ма имеет единственное реш-е полученное по формулам:
Хi =  , где ∆-опред-ль м-цы А; ∆ i -опред-ль получ-й из опред-ля м-цы А заменой i -го столбца на столбец свободных членов В
, где ∆-опред-ль м-цы А; ∆ i -опред-ль получ-й из опред-ля м-цы А заменой i -го столбца на столбец свободных членов В
М-д Гаусса: Этот м-д можно использ-ть для реш-я любых сис-м ЛАУв том числе и тех, у кот-х число урав-ний ≠ числу неизвестных(т ≠ п)
Вопрос7. Теорема Кронекера-Капелли о совместности системы ЛАУ.
Пусть дана матрица общего вида порядка m ´ n:
А= 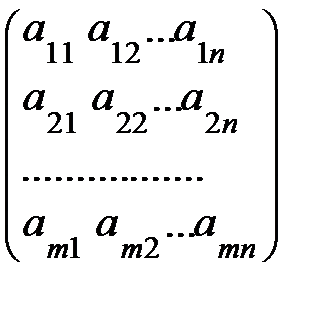 .
.
Обозначим строки матрицы через 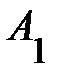 ,
, 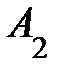 ,…,
,…, 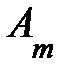 :
: 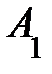 =
= 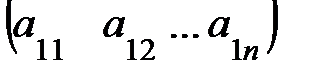 ,
, 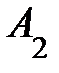 =
= 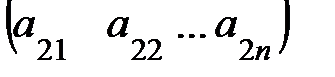 , …,
, …, 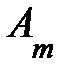 =
= 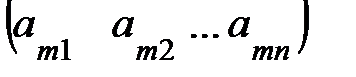
Пусть: 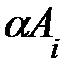 =
= 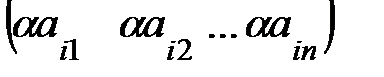 ,
, 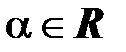 ;
; 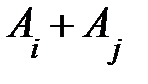 =
= 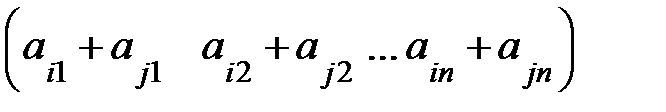
Тогдасумма  +
+ 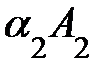 +…+
+…+ 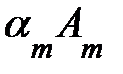 ,
, 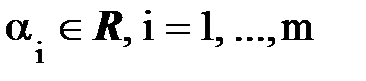 , будет наз. линейной комбинацией строк
, будет наз. линейной комбинацией строк 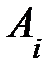 (
(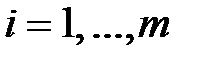 ) м-цы А.
) м-цы А.
Если сущ-ют числа 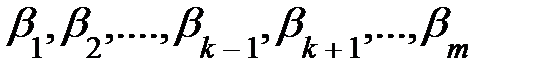 ,такие что
,такие что 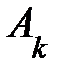 =
= 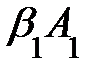 +
+ 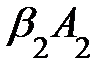 +…+
+…+ 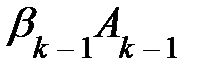 +
+ 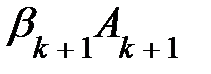 +...+
+...+ 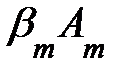 , то говорят, что строка
, то говорят, что строка 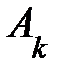 выражается ч-з остальные строки
выражается ч-з остальные строки 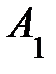 ,
, 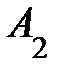 , …,
, …, 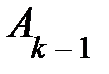 ,
, 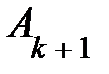 , …,
, …, 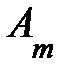 . Строки
. Строки 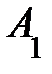 ,
, 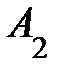 , …,
, …, 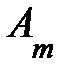 наз-ся линейно зависимыми, если существуют числа
наз-ся линейно зависимыми, если существуют числа
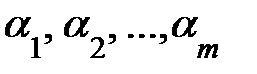 , не все одновременно равные нулю, что
, не все одновременно равные нулю, что  +
+ 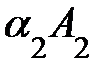 +…+
+…+ 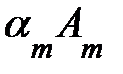 =0, где 0=(0 0 …0). Если же данное равенство выполняется лишь когда все числа
=0, где 0=(0 0 …0). Если же данное равенство выполняется лишь когда все числа 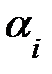 =0,
=0, 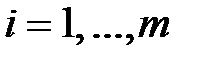 , то говорят, что строки
, то говорят, что строки 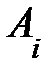 ,
, 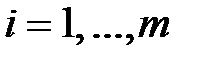 , линейно независимы. Заметим, что, если строки линейно зависимы, то, по крайней мере, одна из них выражается ч-з остальные. Если же строки линейно независимы, то ни одна строка не выражается ч-з остальные. Аналогично вводится понятие линейной зависимости и независимости столбцов.
, линейно независимы. Заметим, что, если строки линейно зависимы, то, по крайней мере, одна из них выражается ч-з остальные. Если же строки линейно независимы, то ни одна строка не выражается ч-з остальные. Аналогично вводится понятие линейной зависимости и независимости столбцов.
Для того, чтобы система линейных алгебраических уравнений была совместной (то есть имела решение), необходимо и достаточно, чтобы ранг исходной матрицы системы совпадал с рангом расширенной матрицы, то есть r(A) = r(С).
1)если r(A) = r(С)= n, где n – число неизвестных системы, то данная система имеет единственное решение;
2)если r(A) = r(С) = k < n, то система имеет бесконечное множество решений;
3)если r(A) ≠ r(С), то система несовместна, то есть не имеет решений.
Если число неизвестных > числа урав-й, то сис-ма либо не имеет реш-й, либо имеет их бесконечное множ-во (если r(A)=r(С)=k <n.)
Вопрос 8. Формулы Крамера решения систем ЛАУ.
Рассмотрим еще один метод решения системы (1) 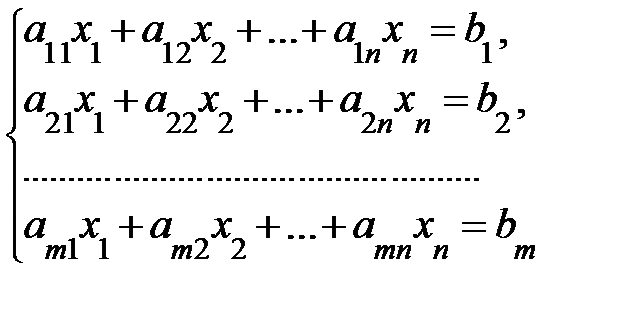
Пусть, как и ранее, n = m.
Тогда из формулы (3) имеем: Х= 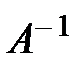 × В
× В 
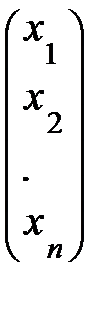 =
= 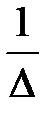
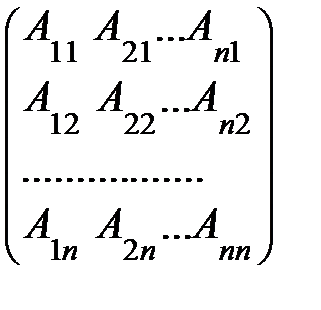
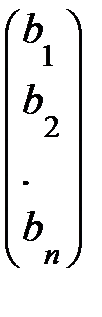 =
= 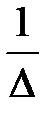
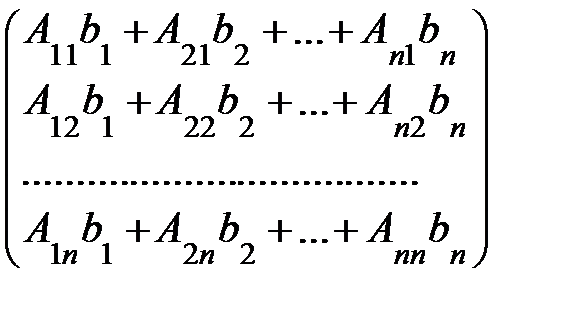
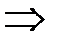
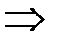
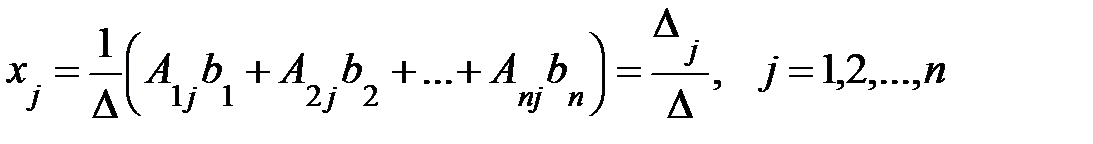 . (4)
. (4)
В формуле (4)  = det A – главный определитель системы (1),
= det A – главный определитель системы (1),
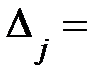
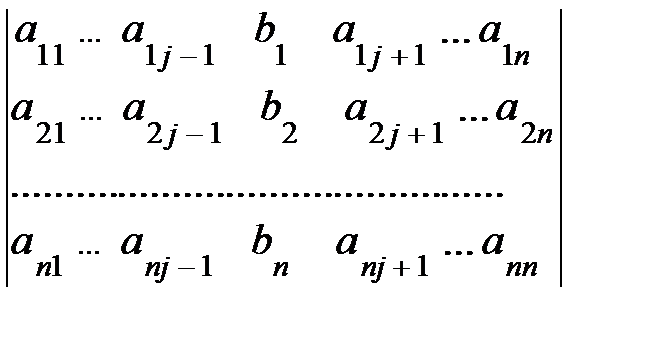
(разлагаем по j-му столбцу)= 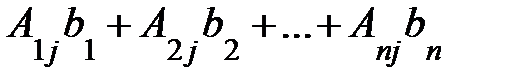 ;
; 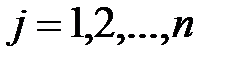 , – побочные опред-ли сис-мы (1).
, – побочные опред-ли сис-мы (1).
Они получаются из главного определителя заменой соответствующего j-го столбца столбцом свободных членов. Формулы (4) называются формулами Крамера.
1.Для матрицы А системы уравнений вычислить ее главный определитель  = det A.
= det A.
2.Последовательно,заменяя каждый столбец м-цы А столбцом свободных членов, получить побочные опред-ли 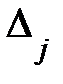 ,
, 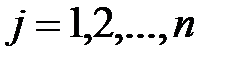
3. а)Если  ≠ 0, то по формулам (4) определить единственное решение системы (1):
≠ 0, то по формулам (4) определить единственное решение системы (1): 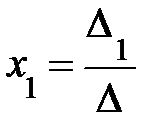 ,
, 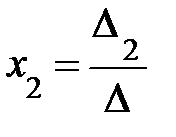 , ….,
, …., 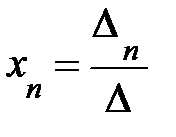 .
.
б) Если  =0, а хотя бы один из побочных опред-лей
=0, а хотя бы один из побочных опред-лей 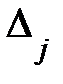 ≠0, то исходная сис-ма (1) несовместна, т. е. не имеет решений
≠0, то исходная сис-ма (1) несовместна, т. е. не имеет решений
в) Если  =
= 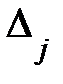 = 0,
= 0, 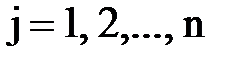 , то исходная система (1) имеет бесконечное множество решений.
, то исходная система (1) имеет бесконечное множество решений.
Вопрос 9 Метод Гаусса решения систем ЛАУ.
Метод Гаусса применим к любой сис-ме ЛАУ. Иногда этот м-д наз-ют методом последовательного исключения неизвестных. Заметим, что при использовании этого метода мы также автоматически будем вычислять ранг матрицы системы.
Итак, пусть задана система m ЛАУс n неизвестными: 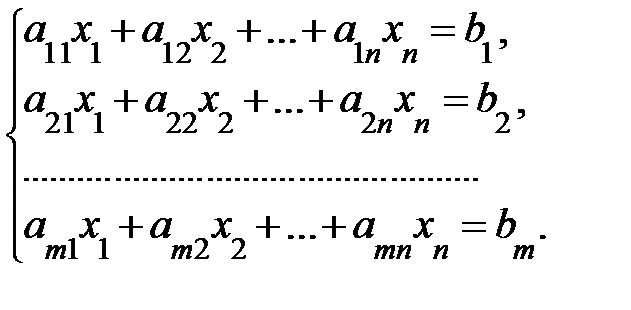 (6 )
(6 )
В матрич-м виде сис-ма (6) запис-ся АХ=В, где А – прямоуг-я м-ца размера m´n: А= 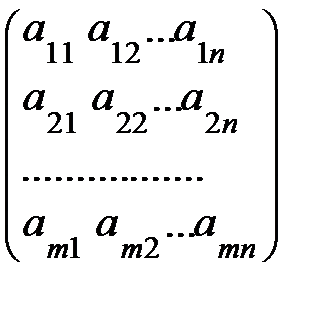 , а,
, а,
Х и В – м-цы-столбцы: Х= 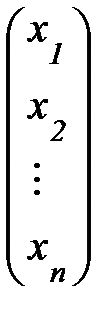 ,В=
,В= 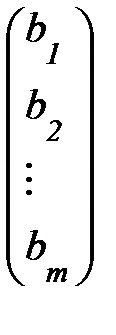 .
.
Если в рез-те преобраз-й м-цы сис-мы получ-я треуг-я м-ца, то сис-ма будет иметь вид: 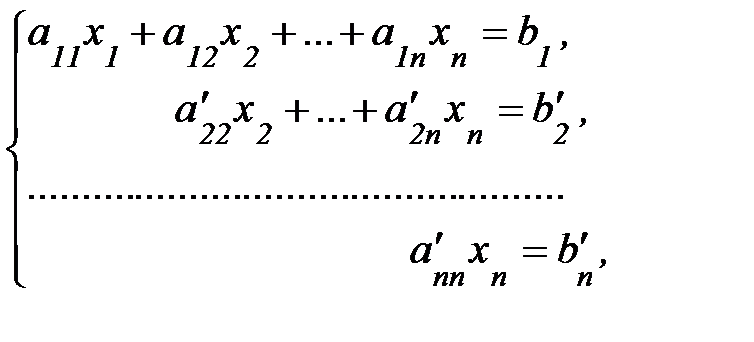
где 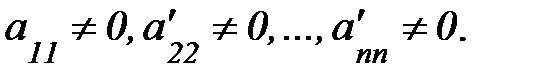
Из последнего урав-я можно найти 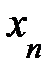 , а затем, подставляя найденное
, а затем, подставляя найденное 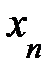 в предпоследнее урав-е, найти
в предпоследнее урав-е, найти 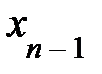 и т.д. В итоге будем иметь единственное решение
и т.д. В итоге будем иметь единственное решение 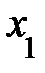 ,
, 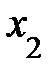 , …,
, …, 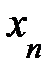 . В этом случае ранг матрицы А системы уравнений равен n.
. В этом случае ранг матрицы А системы уравнений равен n.
Если в рез-те преобраз-й м-цы сис-мы получится трапециевид-я м-ца, то сис-ма примет вид: 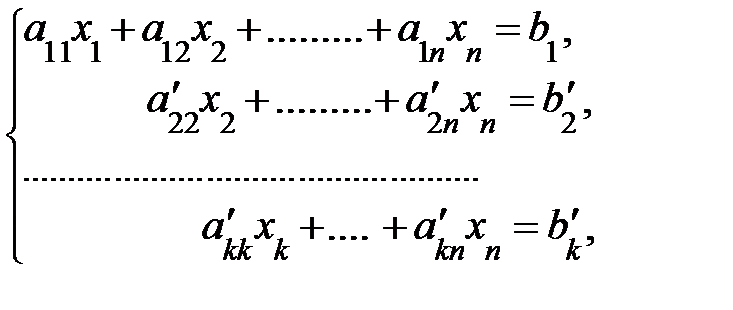
где 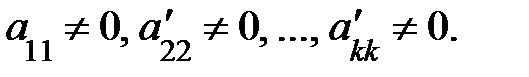
В этом случае k<n, следоват-но, сис-ма урав-й будет неопределенной, т. е. будет иметь бесконечное множество решений, т. к. она содержит n – k свободных переменных: 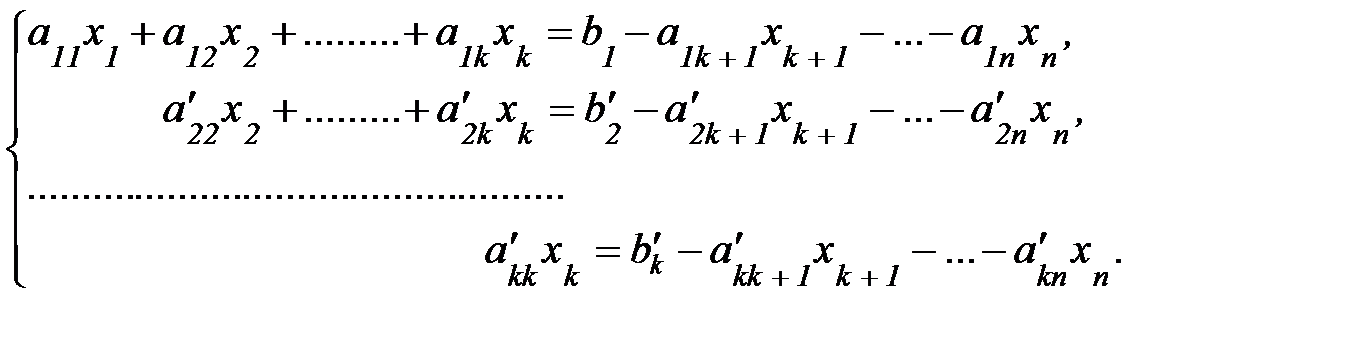
Придавая свободным переменным 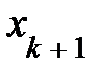 ,
, 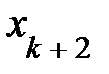 , …,
, …, 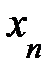 произвольные значения, будем иметь каждый раз новое реш-е исходной сис-мы урав-й, т.е. реш-й будет бесконечное множ-во. В этом случае ранг матрицы А системы равен k.
произвольные значения, будем иметь каждый раз новое реш-е исходной сис-мы урав-й, т.е. реш-й будет бесконечное множ-во. В этом случае ранг матрицы А системы равен k.
Если в рез-те преобразований получено урав-е, в кот. коэф-ты при всех неизвестных = 0, а свободный член отличен от нуля, то такая система будет несовместной, то есть не иметь решения.
Следует отметить, что треугольная или трапециевидная форма системы уравнений получалась ввиду предположения, что коэффициенты 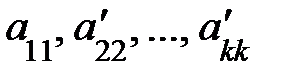 отличны от нуля. Если же какой-либо из этих коэф-в = 0, то система уравнений приобретет треугольную или трапециевидную форму лишь после надлежащего изменения нумерации неизвестных.
отличны от нуля. Если же какой-либо из этих коэф-в = 0, то система уравнений приобретет треугольную или трапециевидную форму лишь после надлежащего изменения нумерации неизвестных.
Метод Гаусса применяется и для однородных систем ЛАУ. В этом случае, если получаем треугольный вид сис-мы урав-й, то она будет иметь единственное (нулевое) решение 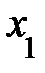 =
= 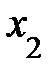 = …=
= …= 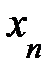 = 0, если же получаем трапециевидный вид системы, то будем иметь бесконечное множество решений.
= 0, если же получаем трапециевидный вид системы, то будем иметь бесконечное множество решений.
При решении системы ЛАУметодом Гаусса удобно выписать расширенную матрицу системы и все преобразования выполнять над строками и столбцами расширенной матрицы.
Вопрос 10. Скалярные и векторные величины. Линейные операции с векторами.
Скалярные величины - величины, которые определяются только числовыми значениями. Например: масса, площадь, длина отрезка, температура.
Если величина, кроме числового значения характеризуется еще и направлением, то она называется векторной величиной или просто вектором. Например: сила, скорость, ускорение. Следовательно, вектор полностью определяется числом и направлением. Геометрически вектор изображают отрезком, длина которого соответствует его числовому значению, а для указания направления используют стрелку.
В

А
Обозначают вектор 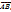 где А – начало вектора, В – конец вектора, или просто
где А – начало вектора, В – конец вектора, или просто  . Заметим, что т. к. длина отрезка соответствует числовому значению вектора, то это числовое значение наз-ют длиной или модулем вектора и обозначают
. Заметим, что т. к. длина отрезка соответствует числовому значению вектора, то это числовое значение наз-ют длиной или модулем вектора и обозначают 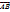 или
или  .
.
Два вектора будем называть равными, если они имеют одно и то же направление и одинаковую длину. Вектор 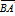 называется противоположным вектору
называется противоположным вектору 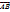 .
. 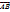 =
= 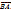 В этом случае пишут
В этом случае пишут 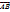 = –
= – 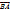 .
.
Нулевым вектором наз-ся век-р, начало и конец кот-го совпадают. Его обозначают  . Заметим, что модуль нулевого вектора равен 0, а направление не определено.
. Заметим, что модуль нулевого вектора равен 0, а направление не определено.
Единичный вектор - вектор, длина кот-го = единице.
2 Век-ра наз-ют коллинеарными, если онт лежат на одной и той же прямой, или  -х прямых
-х прямых
Векторы ‖-ые одной и той же плоскости, наз. компланарными.
Одним из самых важных св-в вектора явл-ся то, что его можно перемещать‖-но самому себе в любую точку плоскости или пространства. (Поэтому коллинеарные векторы всегда можно перенести на одну прямую, а компланарные на одну плоскость).
Углом  = (
= (  ,
,  ) между векторами
) между векторами  и
и  называется угол при вершине
называется угол при вершине  в Δ
в Δ 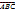 , где
, где  =
= 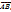
 =
= 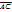 .
.
В

Следовательно, 0 ≤  ≤
≤ 
А С
 ^
^
Два вектора  и
и  считаются ортогональными (перпендикулярными), если.
считаются ортогональными (перпендикулярными), если. 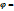 (
(  ,
,  ) =
) =  .Обозначают
.Обозначают 

 .В частности
.В частности 

 ,где
,где  – любой вектор.
– любой вектор.
Линейными операциями над векторами называют сложение, вычитание, умножение вектора на число.
1) Суммой векторов  и
и  называют третий вектор
называют третий вектор  , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец – с концом вектора
, а конец – с концом вектора  при условии, что вектор
при условии, что вектор  отложен из конца вектора
отложен из конца вектора  . Вектор
. Вектор  получается по правилу треугольника или параллелограмма.
получается по правилу треугольника или параллелограмма.
 2015-04-20
2015-04-20 1645
1645