И правой частью специального вида.
Любую правую часть специального вида неоднородного ЛДУ формирует число 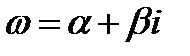 .
.
Выпишем общий вид правой части 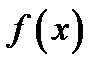 ЛДУ (2.1)
ЛДУ (2.1)
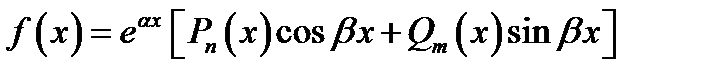 (3.1)
(3.1)
Здесь 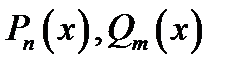 заданные многочлены степени
заданные многочлены степени 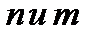 соответственно. Частное решение, в этом случае ищется в виде
соответственно. Частное решение, в этом случае ищется в виде
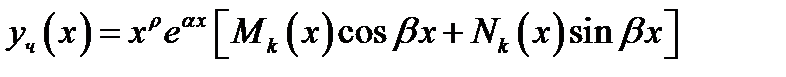 (3.2)
(3.2)
Здесь
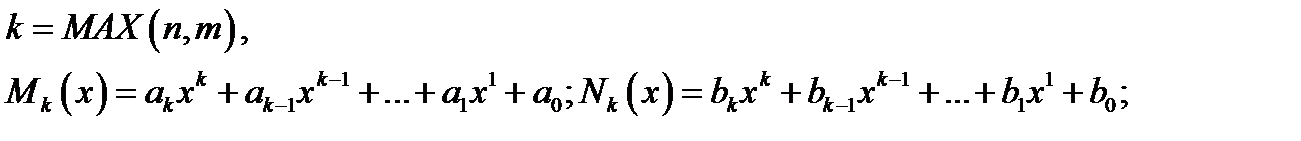
с неопределёнными коэффициентами 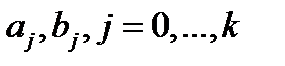 . Показатель степени
. Показатель степени 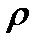 зависит от
зависит от
вида корней характеристического уравнения.
Обозначим 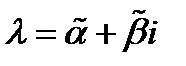 .
.
Сведём виды частных решений для различных правых частей специального вида в таблицу.
Таблица 1.
| № | Правая часть 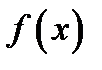
| Корни характеристического уравнения | Вид частного решения |
| I | 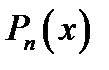
| 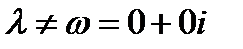
| 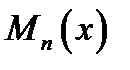
|
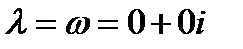 ,кратности ,кратности 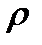
| 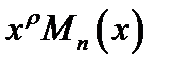
| ||
| II | 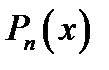 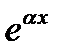
| 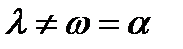
| 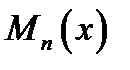 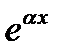
|
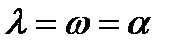 ,кратности ,кратности 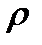
| 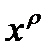 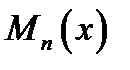 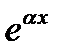
| ||
| III | 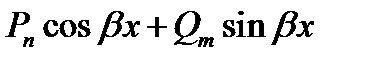
| 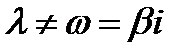
| 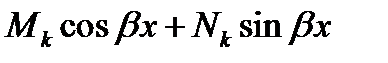
|
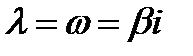 ,кратности ,кратности 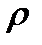
| 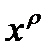 ( (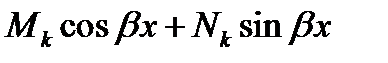 ) )
| ||
| IV | 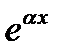 [ [ 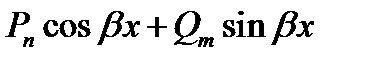 ] ]
| 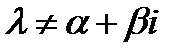
| 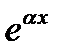 [ [ 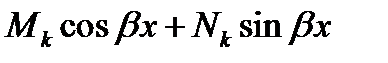 ] ]
|
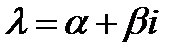 ,кратности ,кратности 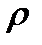
| 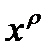 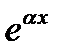 [ [ 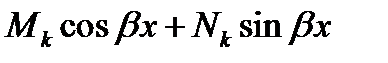 ] ]
|
Пример 1. Найти частное решение неоднородного ЛДУ 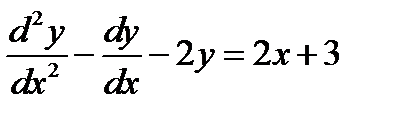 .
.
Решение. Правая часть ЛДУ является многочленом первой степени 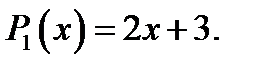
Следовательно 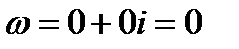 .
.
1 шаг. Находим корни характеристического уравнения 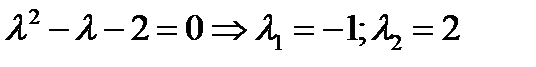 . Ни один из корней не совпадает с
. Ни один из корней не совпадает с 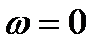 . Согласно таблице 1, ищем частное решение в виде
. Согласно таблице 1, ищем частное решение в виде 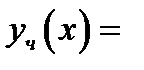
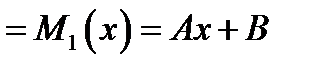 с неизвестными коэффициентами
с неизвестными коэффициентами 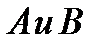 . Чтобы их определить подставляем
. Чтобы их определить подставляем 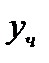 в уравнение и подбираем
в уравнение и подбираем 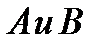 так, чтобы
так, чтобы 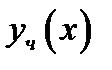 стало решением
стало решением
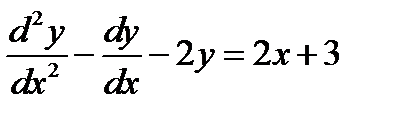 .
. 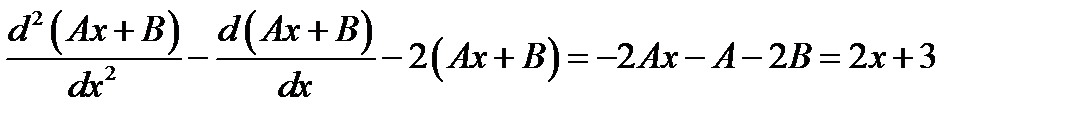
2 шаг. Отсюда 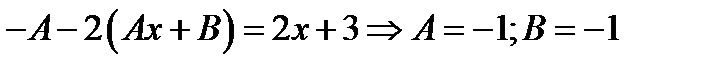 .
.
Ответ: 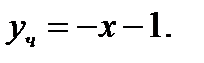
Пример 2. Найти частное решение неоднородного ЛДУ 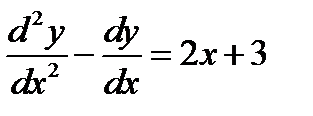 .
.
Решение. Правая часть ЛДУ является многочленом первой степени 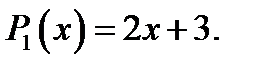 Следовательно
Следовательно 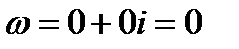 .
.
1 шаг. Находим корни характеристического уравнения 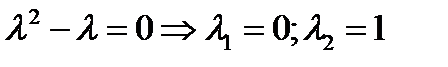 .
.
Один корень совпадает с 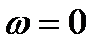 . Согласно таблице 1, ищем частное решение в виде
. Согласно таблице 1, ищем частное решение в виде
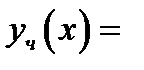
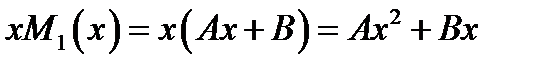 с неизвестными коэффициентами
с неизвестными коэффициентами 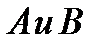 . Чтобы их определить подставляем
. Чтобы их определить подставляем 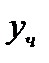 в уравнение и подбираем
в уравнение и подбираем 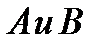 так, чтобы
так, чтобы 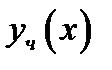 стало
стало
решением 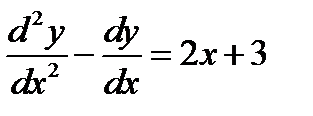 .
.
2 шаг. 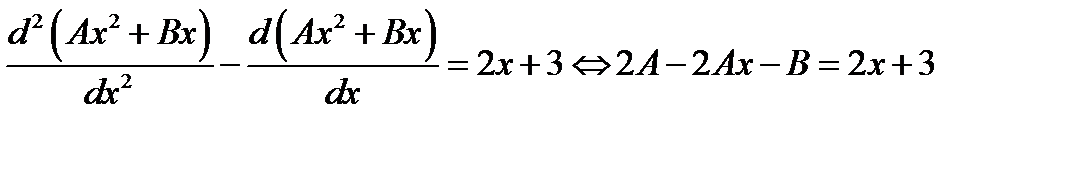
Отсюда 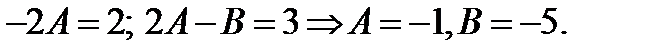
Ответ: 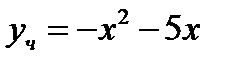 .
.
Пример 3. Найти частное решение неоднородного ЛДУ 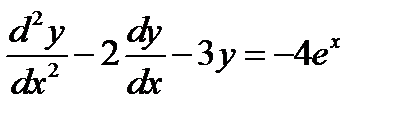 .
.
Решение. По виду правой части определяем 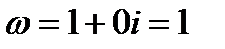 .
.
1 шаг. Находим корни характеристического уравнения 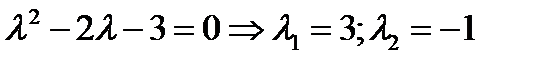 .
.
Ни один из корней не совпадает с 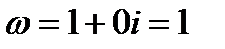 . Согласно таблице 1, ищем частное решение в
. Согласно таблице 1, ищем частное решение в
виде 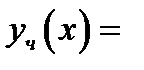
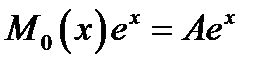 с неизвестным коэффициентом
с неизвестным коэффициентом 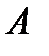 . Чтобы
. Чтобы
его определить подставляем 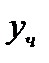 в уравнение и подбираем
в уравнение и подбираем 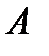 так, чтобы
так, чтобы 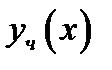 стало
стало
решением 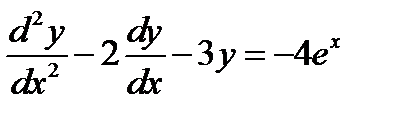 .
.
2 шаг. Определяем 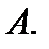
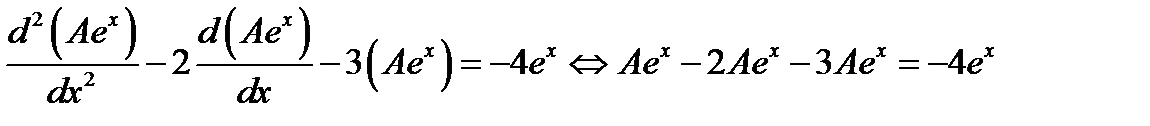
Отсюда 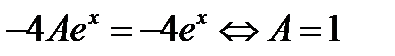
Ответ: 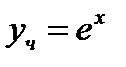 .
.
Пример 4. Найти частное решение неоднородного ЛДУ 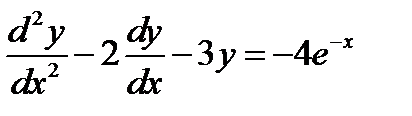 .
.
Решение. 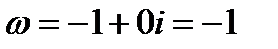 .
.
1 шаг. Находим корни характеристического уравнения 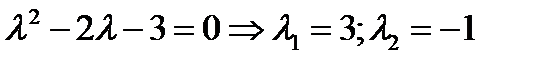 .
.
Один из корней совпадает с 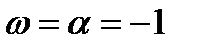 . Согласно таблице 1, ищем частное решение в
. Согласно таблице 1, ищем частное решение в
виде 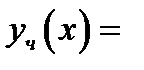
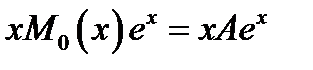 с неизвестным коэффициентом
с неизвестным коэффициентом 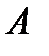 . Чтобы
. Чтобы
его определить подставляем 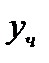 в уравнение и подбираем
в уравнение и подбираем 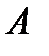 так, чтобы
так, чтобы 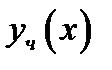 стало
стало
решением 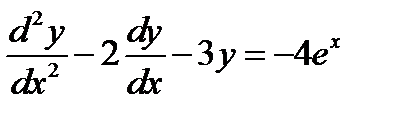 .
.
2 шаг.
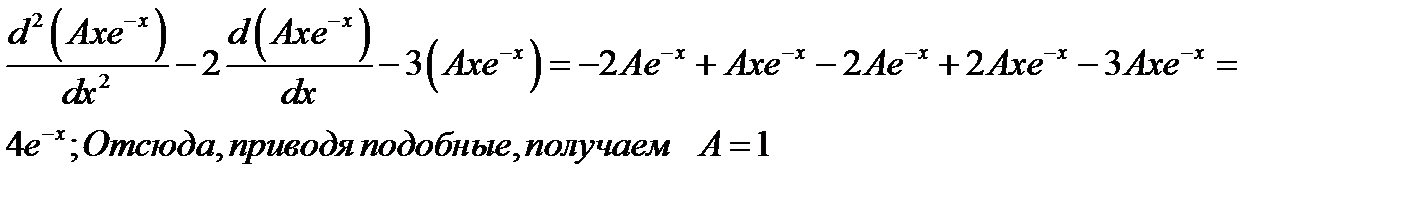
Ответ: 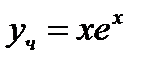 .
.
Пример 5. Найти частное решение неоднородного ЛДУ 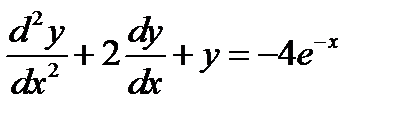 .
.
Решение. 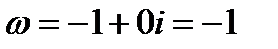 .
.
1 шаг. Находим корни характеристического уравнения 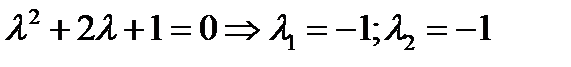 .
.
Оба корня совпадают с 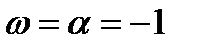 . Согласно таблице 1, ищем частное решение в
. Согласно таблице 1, ищем частное решение в
виде 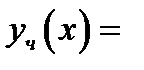
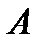
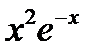 с неизвестным коэффициентом
с неизвестным коэффициентом 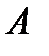 . Чтобы
. Чтобы
его определить подставляем 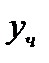 в уравнение и подбираем
в уравнение и подбираем 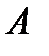 так, чтобы
так, чтобы 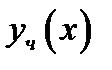 стало
стало
решением 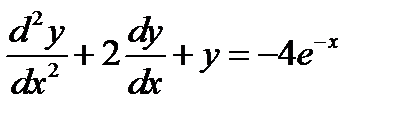 .
.
2 шаг. 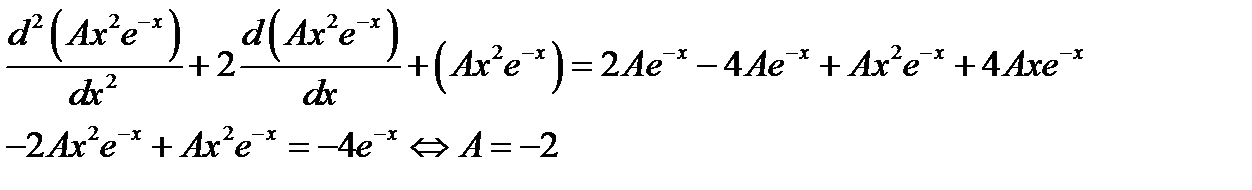
Ответ: 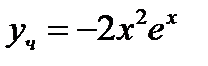 .
.
Пример 6. Найти частное решение неоднородного ЛДУ 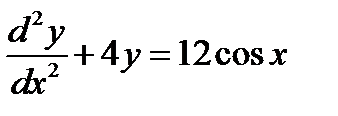 .
.
Решение. Правая часть ЛДУ имеет вид 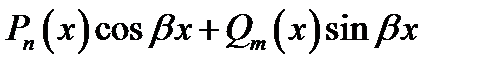 ,
, 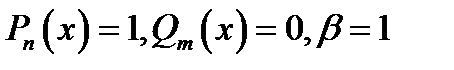
Следовательно 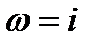 .
.
1 шаг. Находим корни характеристического уравнения 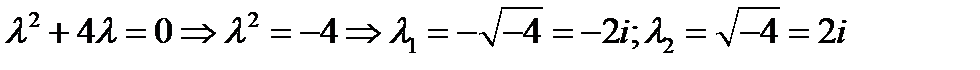 .
.
Ни один из корней не совпадает с 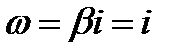 . Согласно таблице 1, ищем частное решение в
. Согласно таблице 1, ищем частное решение в
виде 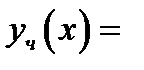
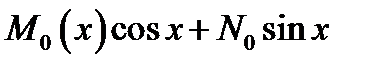 , где
, где 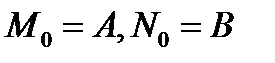 . Числа
. Числа 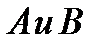 неизвестны. Чтобы
неизвестны. Чтобы
их определить подставляем 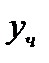 в уравнение и подбираем
в уравнение и подбираем 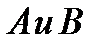 так, чтобы
так, чтобы 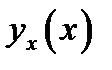 стало
стало
решением 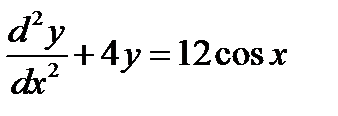 .
.
2 шаг. 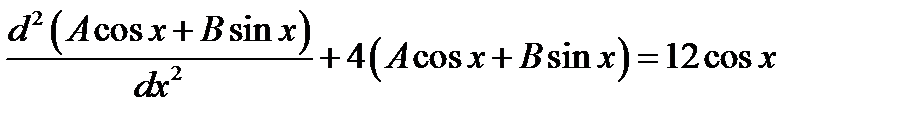 . Дифференцируя, получаем
. Дифференцируя, получаем
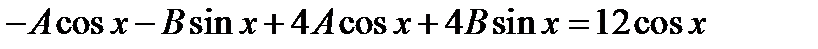 ;
;
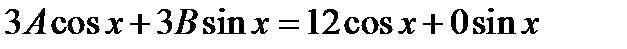 . Последнее равенство будет выполнено, тогда и только тогда если
. Последнее равенство будет выполнено, тогда и только тогда если 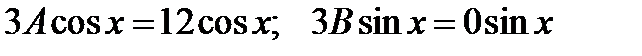 . Откуда
. Откуда 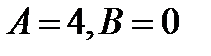 .
.
Ответ: 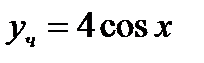 .
.
Пример 7. Найти частное решение неоднородного ЛДУ 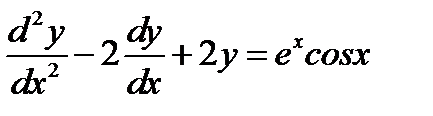 .
.
Решение. Правая часть ЛДУ имеет вид 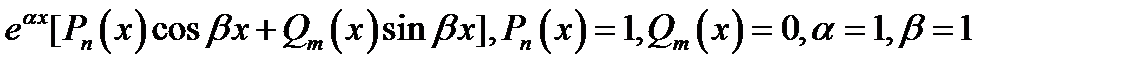 .Следовательно
.Следовательно 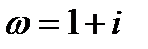
1 шаг. Находим корни характеристического уравнения 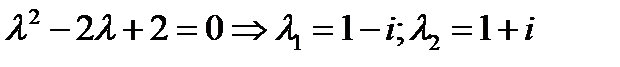 .
.
Один корень совпадает с 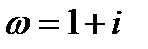 . Согласно таблице 1, ищем частное решение в
. Согласно таблице 1, ищем частное решение в
виде 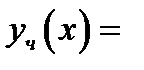
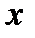
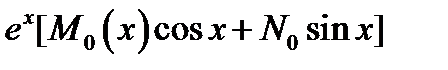 .Здесь
.Здесь 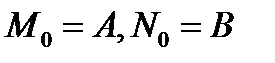 . Числа
. Числа 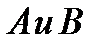 неизвестны. Чтобы их определить подставляем
неизвестны. Чтобы их определить подставляем 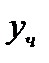 в уравнение и подбираем
в уравнение и подбираем 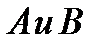 так, чтобы
так, чтобы 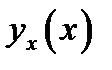 стало решением
стало решением 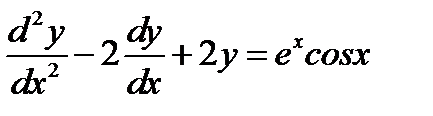 . Имеем
. Имеем
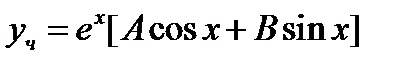 ,
, 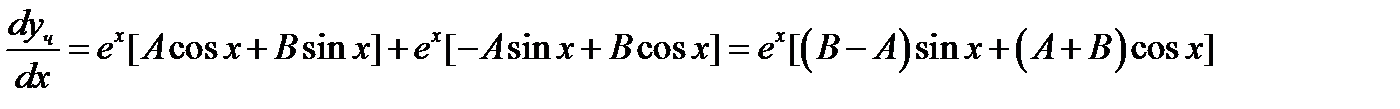 ,
,
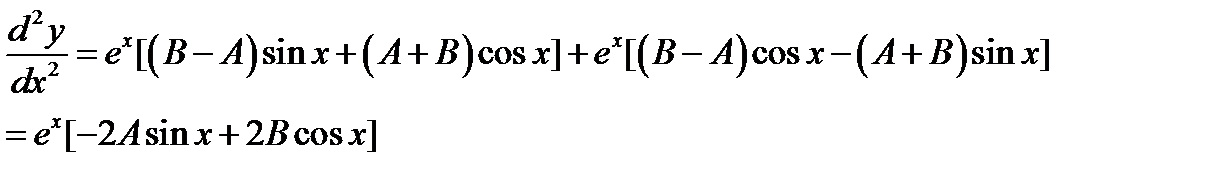
2 шаг.
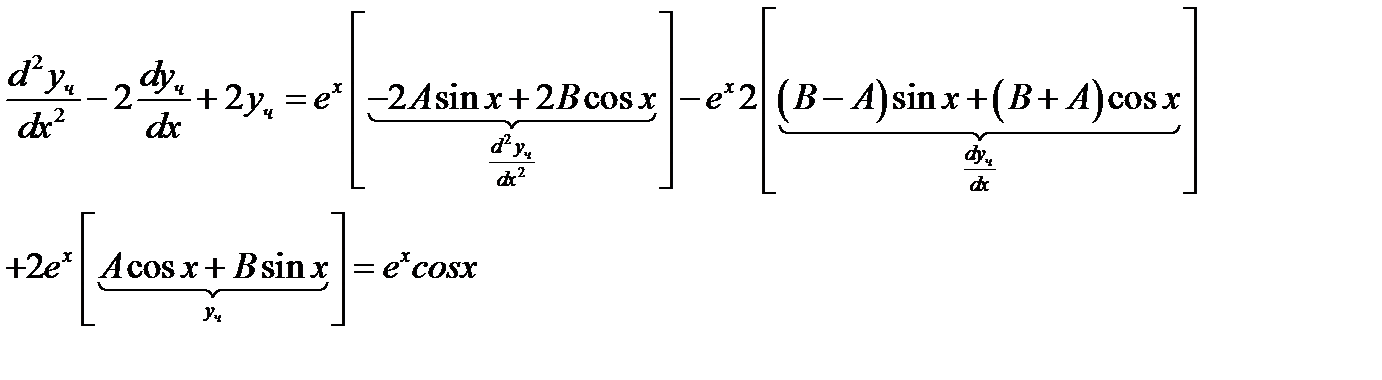
Приводя подобные слагаемые, получаем 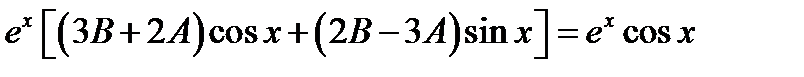 .
.
Сокращая обе части равенства на 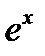 , будем иметь
, будем иметь 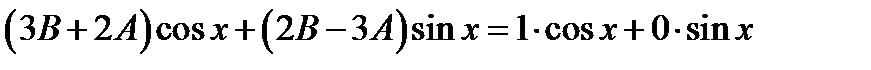 . Чтобы получилось тождество, нужно
. Чтобы получилось тождество, нужно
решить систему уравнений 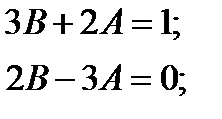 Решая систему, получаем
Решая систему, получаем 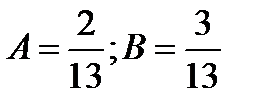 .
.
Ответ: 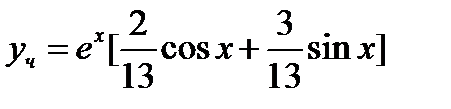 .
.
 2015-04-30
2015-04-30 1783
1783








