Однородные ОДУ первого порядка

Лекция 5.

Тема. Некоторые типы ОДУ первого и второго порядков.

Уравнения типа Бернулли

Данные ОДУ первого порядка имеют вид .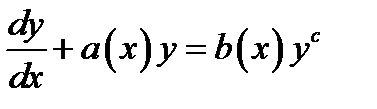

Правило нахождения общего решения.

Уравнение сводится к линейному уравнению заменой .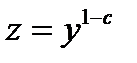

Пример 3. Найти общее решение ОДУ первого порядка, типа Бернулли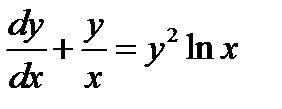

Решение.В нашем случае =2.Заменяем переменную .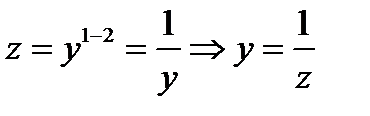

Подставляя замену в уравнение, получаем уравнение

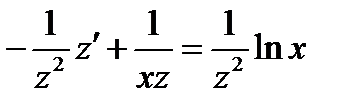. Умножим обе части ОДУ на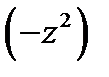

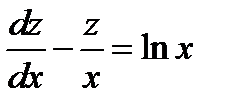. Получили линейное уравнение. Находим интегрирующий множитель

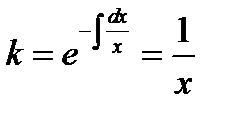. Умножая обе части ОДУ на множитель 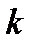, получаем уравнение .

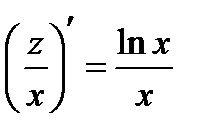Интегрируя обе части, определяем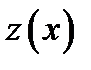

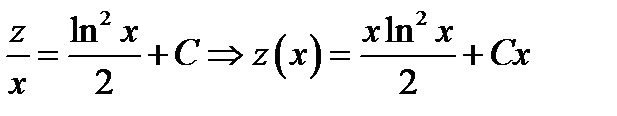.Возвращаясь к переменной 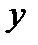, получаем общее решение

данного уравнения Бернулли

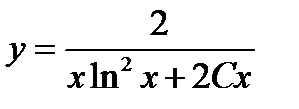
Однородные ОДУ первого порядка.

Определение 7.1. Функция 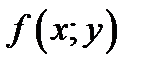, зависящая от двух переменных 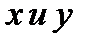называется однородной функцией, если для любого справедливо равенство .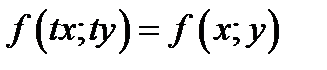

Упражнение 7.1. Проверить какие из данных функций являются однородными

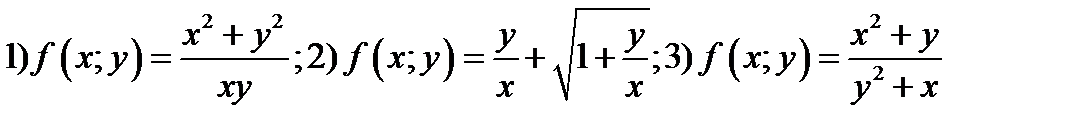
Ответы: первые две являются, третья нет.

Правило нахождения общего решения ОДУ первого порядка с однородной функцией 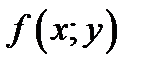в правой части.

Постановка задачи. Пусть требуется решить ОДУ

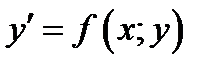(7.1)

Правая часть (7.1) является однородной функцией, то есть для любого

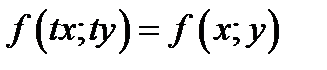(7.2)

Заменяем переменную 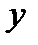на новую переменную по правилу

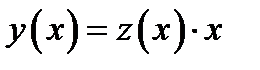(7.3)

Дифференцируя (7.3) получаем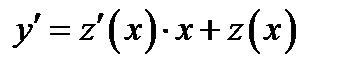

Подставляя полученные замены в ОДУ (7.1) получаем ОДУ

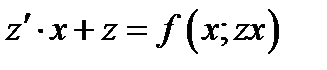(7.5)

Замечая, что в силу определения 7.1

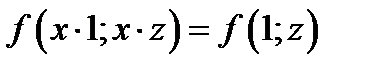получаем после такой замены

ОДУ с разделяющимися переменными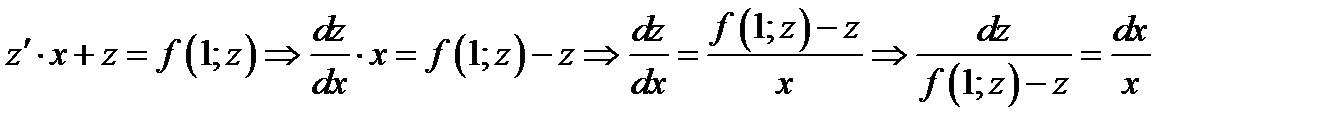

Интегрируя обе части ОДУ, получаем общий интеграл

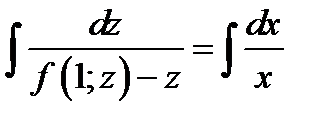
Пример 3. Решить начальную задачу Коши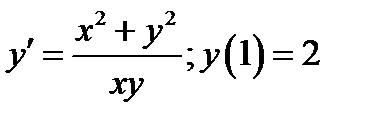

Решение. Проверим, является ли выражение 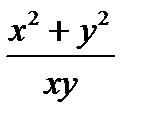однородной функцией.

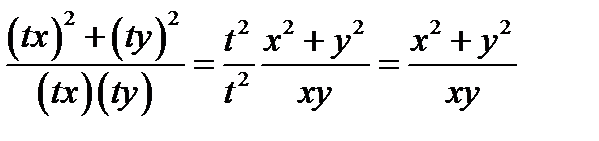. Данное выражение является однородной функцией

согласно определению 7.1. Заменяем переменную 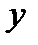на новую переменную по правилу

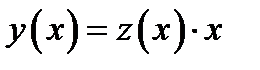, (7.3)

а переменную 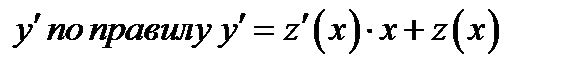и подставляем замену в уравнение

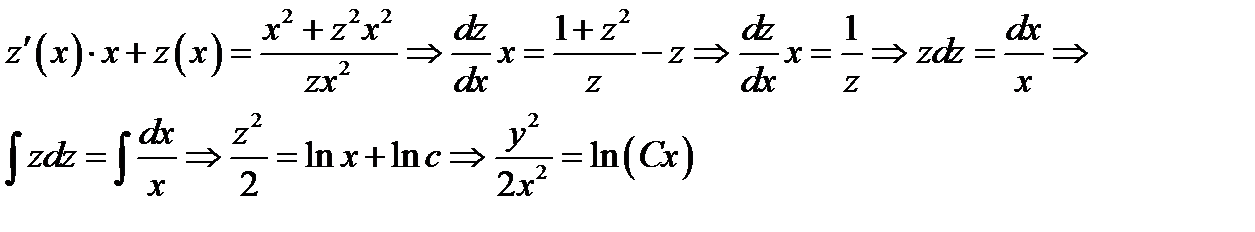
Выписываем общий интеграл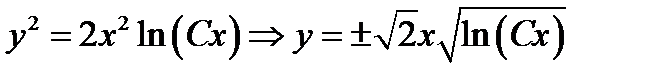

Так как по условию. 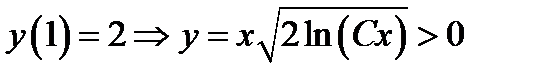.Чтобы выбрать подходящую постоянную С подставляем 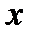=1, а 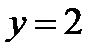в полученное общее решение и получаем решение начальной задачи

.

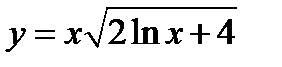Упражнение 7.2. Решить начальные задачи

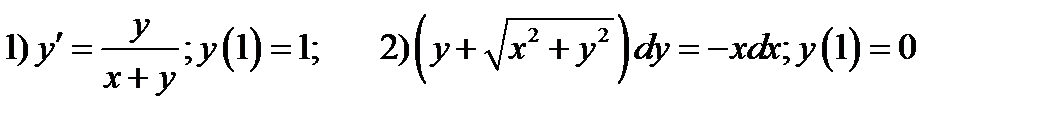
Ответы: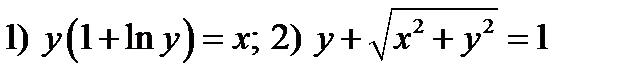

ОДУ первого порядка в полных дифференциалах.

Напомним, что если у функции 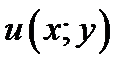существуют непрерывные частные производные 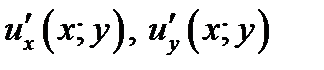, то полным дифференциалом мы называем выражение

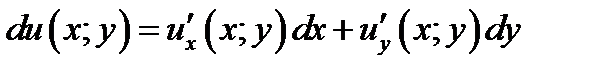(7.6)

Пусть в некоторой области 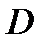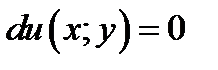, тогда в этой же области

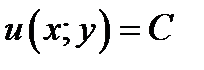, (7.7)

где 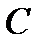произвольная постоянная.

Определение 7.2. Обыкновенным дифференциальным уравнением первого порядка называется

уравнение вида

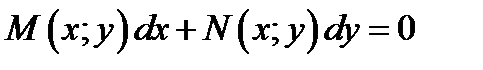(7.8)

удовлетворяющего условию

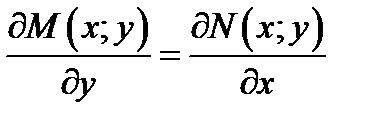(7.9)

Теорема 7.1. Если ОДУ удовлетворяет условию (7.9), то выражение (7.8) является полным дифференциалом (7.7) некоторой функции 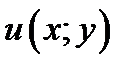, то есть

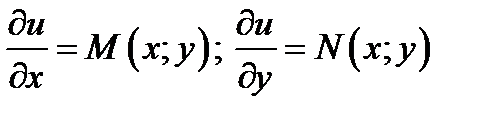(7.10)