Понятие функции

Рассмотрим множество X элементов х и множество Y элементов у. Если каждому элементу х 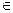Х поставлен в соответствие единствен­ный элемент у 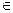Y, обозначаемый у =f(x), то говорят, что на множестве X задана функция у =f(x) со значениями в множестве Y. Элементы х 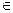Х называются значениями аргумента, а элементы у 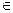Y - значениями функции. Множество X называется областью определения функции, множество всех значений функции - областью значений этой функ­ции.

Функцию, заданную на множестве X, называют также операто­ром, заданным на множестве X, и обозначают символом f.

В случае, когда X и Y - числовые множества, соответствующие функции называют числовыми функциями..

Значение, которое функция у = f(x) принимает при х = а, обозначается через f(x).

К простейшим областям определения функций относится отре­зок, интервал, полуинтервалы или совокупность указан­ных интервалов. Например, для функции 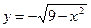областью опре­деления является отрезок [-3, 3], а областью ее значений - отрезок [-3, 0], для функции 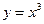область определения и область значений совпадают с интервалом (- , ).

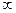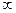К традиционным основным способам задания функции относят­ся: аналитический (с помощью одной или нескольких формул), графи­ческий (с помощью графика), табличный (с помощью таблицы значе­ний).

Функция, заданная формулой

у =f(x), (1)

правая часть, которой не содержит у, называется явной функцией.

Обратимся к функции (1). Каждому х 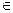Х по определенному закону ставится в соответствие единственное значение у 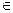Y. С другой стороны, каждому у 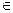Y будет соответствовать одно или несколько зна­чений 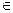х Х.

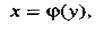В случае, когда каждому у 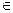Y по некоторому закону соответст­вует только одно значение х 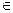Х, получаем функцию

(2)

заданную на множестве Y со значениями в множестве X. Функцию (2) называют обратной функцией по отношению к функции (1). Функции (1) и (2) называются взаимно-обратными.

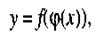Если 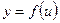, 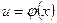- функции своих аргументов, причем об­ласть определения функции f содержит область значений 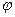, то каждо­му х из области определения функции 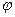соответствует у такое, что 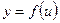, где 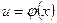. Эта функция, определяемая соответствием

(3)

называется функцией от функции, или сложной функцией.

Функция у =f(x) называется четной, если для любых х и -х из области ее определения выполняется равенство f(-х) =f(х). Функция у = 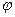(х) называется нечетной, если для любых х и -х из области ее определения выполняется равенство 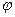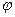(-х) = - (х).

Функция у =f(x) называется периодической, если существует число 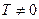такое, что при всех х и х+Т из области ее определения вы­полняется равенство f(х+Т) =f(х). Число Т в этом случае называется периодом функции. Всякая периодическая функция имеет бесконечное множество периодов. Кроме тригонометрических и обратных тригонометрических функций в средней школе изучаются функции: степенная у = х^a (а = соnst), показательная у = a^x (а = соnst), логарифмическая у = 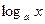(а = соnst). Все эти функции называются основными элементарными функциями.

Элементарными функциями называются функции, которые можно получить из основных элементарных функций с помощью ал­гебраических действий и образования сложных функций. Например, функции 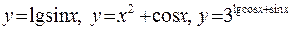и т.д. являются элемен­тарными.

Рассмотрим плоскость, на которой выбрана декартова прямо­угольная система координат.

Графиком функции у =f(x) называется множество точек плос­кости, координаты которых удовлетворяют данной функциональной зависимости.

График функции от непрерывного аргумента представляет собой некоторую линию на плоскости. График функции от дискретного ар­гумента не является линией, он состоит из дискретных точек.

Отметим, что график четной функции симметричен относитель­но оси Оу, график нечетной функции симметричен относительно на­чала координат. Графики взаимно-обратных функций симметричны относительно прямой, на которой лежит биссектриса первого коорди­натного угла.