Дифференциальное уравнение первого порядка в общем случае можно зависать в виде
F(х;у;у') = 0 (1)
Уравнение связывает независимую переменную х, искомую функцию у и ее производную у'. Если уравнение (1) можно разрешить относительно у', то его записывают в виде: у' = f(х,у)
и называют ДУ первого порядка, разрешенным относительно производной. В основном мы будем рассматривать эту форму записи ДУ.
Дифференциальное уравнение первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме: Р(х;у)dx + Q(х;у)dу = 0,
где Р(х; у) и Q (х; у) известные функции. Уравнение (3) удобно тем, что переменные х и у в нем равноправны, т. е. любую из них можно рассматривать как функцию другой. Отметим, что от одного вида записи ДУ можно перейти к другому.
Интегрирование ДУ в общем случае приводит к бесконечному множеству решений (отличающихся друг от друга постоянными величинами). Легко догадаться, что решением уравнения у' = 2х является функция у = х2, а также у = х2 + 1, у = х2 — 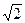 и вообще у = х2 + с, где с-соnst.
и вообще у = х2 + с, где с-соnst.
|
|
|
Чтобы решение ДУ приобрело конкретный смысл, его надо подчинить некоторым дополнительным условиям.
Условие, что при х = х0 функция у должна быть равна заданному числу уо, т. е. у = уо называется начальным условием. Начальное условие записывается в виде
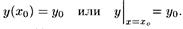
Общим решением ДУ первого порядка называется функция у = φ (х; с), содержащая одну произвольную постоянную и удовлетворяющая условиям:
1. Функция φ (х; с) является решением ДУ при каждом фиксированном значении с.
2. Каково бы ни было начальное условие, можно найти такое значение постоянной с = с0, что функция у =φ (х; с0) удовлетворяет данному начальному условию.
Частным решением ДУ первого порядка называется любая функция у = φ (х; с0), полученная из общего решения у =φ (х; с) при конкретном значении постоянной с = с0.
Если общее решение ДУ найдено в неявном виде, т. е. в виде уравнения Ф(х; у; с) = 0, то такое решение называется общим интегралом ДУ. Уравнение Ф(х: у; со) = 0 в этом случае называется частным интегралом уравнения.
Наиболее простым ДУ первого порядка является, уравнение вида: Р(х)·dx + Q(у)·dу = 0 (1)
В нем одно слагаемое зависит только от х, а другое от у. Иногда такие ДУ называют уравнениями с разделенными переменными. Проинтегрировав почленно это уравнение, получаем:
∫Р(х)·dx + ∫Q(у)·dу = с - его общий интеграл.
Пример 1. Найти общий интеграл уравнения х·dx + у·dу = 0
Решение: Данное уравнение есть ДУ с разделенными переменными. Поэтому ∫х·dx - ∫у·dу = с1, или 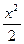 –
– 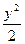 = с1, обозначим
= с1, обозначим 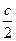 = с1,
= с1,
тогда х2 – у2 = с – общий интеграл ДУ.
Более общий случай описывают уравнения с разделяющимися переменными, которые имеют вид
|
|
|
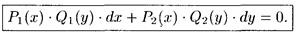 (2)
(2)
Особенность уравнения (2) в том, что коэффициенты при dx и dу представляют собой произведения двух функций (чисел), одна из которых зависит только от х, другая только от у.
Уравнение (2) легко сводится к уравнению (1) путем почленного деления его на Q1(у)·Р2(х)≠0. Получаем:
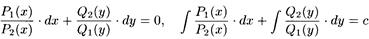 - общий интеграл.
- общий интеграл.
Замечание. При проведении почленного деления ДУ на Q1(у)·Р2(х) могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнение Q1(у)·Р2(х) = 0 и установить те решения ДУ, которые не могут быть получены из общего решения.
Решения дифференциального уравнения, которые не получаются из общего решения ни при каких значениях произвольной постоянной называются частными или особыми. Особые решения могут иметь только те уравнения, для которых нарушаются условия теоремы существования и единственности.
2. Уравнение у" = f1(х) · f2(у) также сводится к уравнению с разделенными переменными. Для этого достаточно представить
у' = 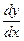 и разделить переменные.
и разделить переменные.
3. Уравнение у' = f(ах + bу + с), где а, b, с — числа, путем замены ах + bу + с = u сводится к ДУ с разделяющимися переменными. Дифференцируя по х, получаем:
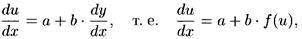
откуда следует 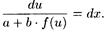
Интегрируя это уравнение и заменяя u на ах + bу + с, получим общий интеграл исходного уравнения.
Пример 2. Решить уравнение: (у+ху) dх+ (х–ху)dу = 0
Решение: Преобразуем левую часть уравнения:
у· (1+ х) dх+ х·(1 – у) dу = 0.
Делим обе части уравнения на ху ≠ 0:
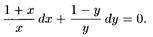
Решением его является общий интеграл х + ℓn ½ х ½ + ℓn ½ у ½ – у = с т.е. ℓn ½ ху ½ + х – у = с. Здесь уравнение Q1(у)·Р2(х) = 0 имеет вид ху=0. Его решения х = 0, у = 0 являются решениями данного ДУ, но не входят в общий интеграл. Значит, решения х = 0, у =0 являются особыми.
Пример 3. Решить уравнение у' = – 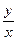 , удовлетворяющее условию у(4) = 1.
, удовлетворяющее условию у(4) = 1.
Решение: 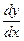 = –
= – 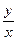 или
или 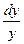 = –
= – 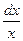 . Проинтегрировав, получим ℓn ½ у ½ = ℓn ½ с ½ – ℓn ½ х ½,
. Проинтегрировав, получим ℓn ½ у ½ = ℓn ½ с ½ – ℓn ½ х ½,
т. е. у =с/х – общее решение ДУ.
Оно геометрически является семейством равносторонних гипербол. Выделим среди них одну, проходящую через точку (4; 1). Подставим х = 4 и у = 1 в общее решение уравнения: 1 = 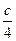 , с = 4.
, с = 4.
Получаем: у = 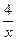 частное решение уравнения у' = –
частное решение уравнения у' = – 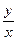 .
.
Пример 4. Найти общее решение ДУ та V' = –k ·V2.
Решение: Приведем данное уравнение к виду (5):
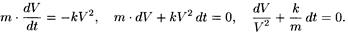
Интегрируем: 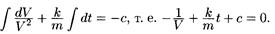 Отсюда
Отсюда 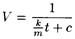 - общее решение.
- общее решение.
 2015-05-20
2015-05-20 1100
1100








