Тема 2. Однородные дифференциальные уравнения

К уравнению с разделяющимися переменными приводятся однородные ДУ первого порядка.

Функция f(х; у) называется однородной функцией n -го порядка, если при умножении каждого ее аргумента на произвольный множитель α вся функция умножится на αⁿ, т. е. f(α·х;α·у)=αⁿ f(х;у).

Например, функция f(х;у) = х² – 2ху - однородная функция второго порядка,

т.к. f(α·х;α·у) = (α·х)² – 2 (α·х)(α·у) = α²·(х²-2ху) = α² f(х;у).

Дифференциальное уравнение у' = f(х;у) = 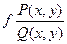(3)называется однородным, если, входящие в него функции Р(х; у) и Q(х;у) - однородные функции одного порядка.

Однородное уравнение преобразуется в уравнение с разделяющимися переменными при помощи замены переменной (подстановки)

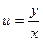или, что то же самое 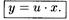(4)

Подставив у = u·x и у′ = u′x + u в уравнение (3) получаем. уравнение с разделяющимися переменными. Найдя его общее решение (или общий интеграл), следует заменить в нем u на .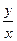

Однородное уравнение часто задается в дифференциальной форме:

Р(х; у)·dx+ Q(х;у)·dy = 0 (5)

Применяем подстановку у = u·x и dy = х·du+u·dx и действуем, как в предыдущем случае.

(Можно также применять подстановку 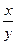= u)

Замечание: уравнение виде у′ = 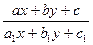приводится к однородному с помощью замен

х =u+α; у = v+β, где α и β – числа, которые подбирают соответствующим образом, чтобы уравнение стало однородным, для упрощения вычисления.

Пример: Найти общий интеграл уравнения: (х²–у²)·dx+2ху·dy=0.

Решение: Данное уравнение однородное, т. к. функции Р(х; у) = х² – у² и

Q (х; у) = 2ху — однородные функции второго порядка.

Пусть у = u·x и dy = х·du+u·dx. Подставляем в исходное уравнение :

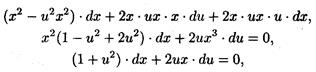
последнее уравнение – с разделяющимися переменными. Делим переменные и интегрируем. Затем заменяя u на у/х, получаем: х² + у² = сх общий интеграл исходного уравнения.

Пример. Найти общий интеграл уравнения (х + 2у + 1)·dx ‒ (2х + у ‒ 1)·dy=0. т.е.

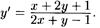
Решение: Положив х = u + α, у = v + β, получаем:

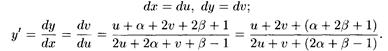
Подберем α и β так, чтобы

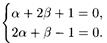
Находим, что α = 1, β = ‒1. Заданное уравнение примет вид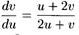

и будет являться однородным. Его решение получается, как это было показано выше, при помощи подстановки v = t·u. Заметим, что, решив его, следует заменить u и v соответственно на х ‒ 1 и у + 1. В итоге получим (у ‒ х +2)³ = с(х+у) - общий интеграл данного уравнения.