Математическое моделирование температурного режима в защищенном грунте

Существует несколько способов моделирования температурных полей в сооружениях защищенного грунта. Наиболее распространенный из них – это метод электротепловой аналогии [32].

Этот метод основан на аналогии между температурным и электрическим полем в замкнутом контуре. С помощью этого метода исследования проводят на объемной и плоской моделях, выполненных из электропроводной среды. Причем исследования на плоских моделях значительно проще и их приводят для получения картины распределения температур в наиболее характерном сечении теплицы [45].

Результатом приведенных в этом разделе математических преобразований у авторов [46] получилось поле, показанное на рисунке 2.1.

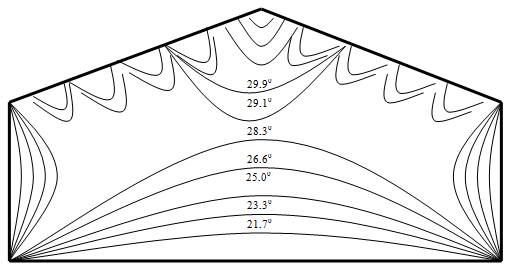
Рисунок 2.1 Температурное поле теплицы, полученное методом электротепловой аналогии

Анализ рисунка 2.1 позволяет сделать вывод, что температура в теплице может быть описана изотермическими линиями, имеющими криволинейный характер, огибающими нагревательные элементы. Для упрощения математического моделирования поверхность почвы в теплице принимают как однородно нагретую плоскость. В этой модели не учитывается влияние скорости воздушных потоков, циркулирующих в рабочем объеме сооружений защищенного грунта.

Целью любого математического моделирования в прикладных задачах является описание существующего какого-либо физического процесса в определенных условиях с целью контроля этого процесса или контроля какой-либо физической величины. Актуальной задачей, для условий производства биологических объектов в защищенном грунте, будет являться математическое моделирования температурного режима таким образом, чтобы при минимальном количестве первичных измерительных преобразователей (ПИП), система управления была способна контролировать эту физическую величину по всему рабочему объему защищенного грунта.

Связь любой математической модели с реальностью осуществляется с помощью цепочки гипотез, идеализаций и упрощений. С помощью математических методов описывается идеальный объект, построенный на этапе содержательного моделирования. Как правило, в математических моделях отбрасывают детали, которые могут заметно и не всегда контролируемо повлиять на результат. Одни и те же уравнения могут служить моделями разного типа. Это зависит от явления, для изучения которого используется модель [51].

Не отступая от классических принципов математического регулирования для описания температурного поля в рабочем объеме сооружений защищенного грунта, примем следующие допущения:

· Поверхность почвы идеально ровная, имеет во всех точках одинаковую температуру, тепловой поток направлен только в направлении от почвы в воздушное пространство теплицы. Следовательно, поверхность почвы можно принять за изотермическую плоскость.

· Боковые ограждающие конструкции имеют однослойную структуру с идеальной тепловой изоляцией. Боковой и шатровый обогрев не влияют на температурное поле в теплице.

· Траектория движения тепловых потоков воздушных масс в поперечном сечении теплицы близка к эллиптической форме. Рассматривать кинематику процесса будем, без выяснения причин, которые определяют движение тепловых масс среды по эллиптическим траекториям.

· Рабочий объем защищенного грунта представим как пространство, ограниченное по бокам плоскостями, а сверху цилиндром, так как, это наиболее близкая геометрическая фигура, которой можно описать теплицу, имеет гладкий контур, а, следовательно – непрерывные первые производные.

Не вызывает сомнения тот факт, что современные сооружения защищенного грунта представляют тела конечных размеров правильной геометрической формы, образованных путем взаимного пересечения неограниченных пластин (рисунок 2.4).

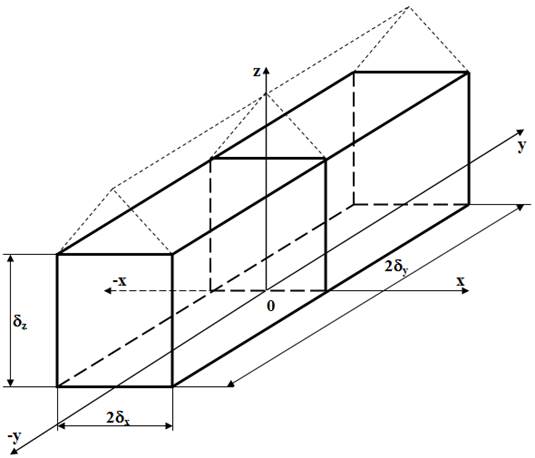
Рисунок 2.4 Сооружение защищенного грунта в виде тела конечных размеров

Если учесть, что в большинстве современных теплиц конек отделен от основного объема механизмом зашторивания с целью снижения тепловых потерь в зимний период и защиты биологических объектов от чрезвычайно сильного солнечного излучения в летний период, то теплица – это параллелепипед конечных геометрических размеров по осям декартовых координат x, y, z.

Если тело образовано пересечением двух плоских пластин, имеющих толщину 2d_x в плоскости x и 2d_y в плоскости y, то поле температур равно:

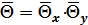. (2.14)

Соответственно для параллелепипеда (рисунок 2.4):

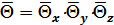. (2.15)

Основываясь на результатах других исследователей, примем, к вниманию, тот факт, что охлаждение оказывает на температурное поле существенное влияние и, следовательно, температурное поле под коньком теплицы ограничивается усеченным полуцилиндром (рисунок 2.5).

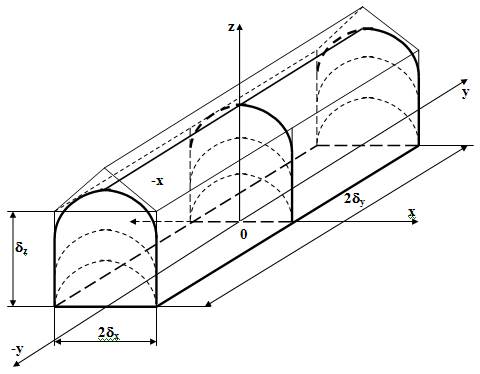
Рисунок 2.5 Теплица в виде усеченного полуцилиндра.

Таким образом, температурное поле в защищенном грунте можно описать как пересечение двух неограниченных пластин по осям x и y, а по оси z цилиндром. На основании этого, формула (2.15) может быть преобразована:

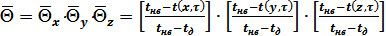, (2.16)

где t_нв – температура наружного воздуха, т.е. окружающей среды;

t_д – температура воздуха в теплице в момент времени τ=0, которая может быть измерена датчиком, установленным в наиболее теплом месте.

Необходимо, также, учесть, что теплица находится в условиях охлаждения, т.е. t_нв < t_д. Следовательно, формулу (2.16) можно представить:

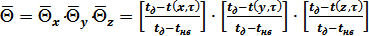, (2.17)

Таким образом, для определения общего температурного поля в защищенном грунте нам необходимо определить температурные поля по каждой оси. Описать температурные поля по осям x и y можно аналогично, т.е. как в неограниченных пластинах, а по оси z цилиндром.