Температурное нестационарное поле в неограниченной пластине

Температурное поле в неограниченной плоской пластине, находящейся в условиях охлаждения:

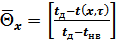, (2.18)

можно определить, используя дифференциальное уравнение нестационарной теплопроводности, которое имеет вид:

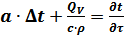, (2.19)

где a – коэффициент температуропроводности, м²/с;

Δt – разница температур, ⁰С;

Q_V – объемная плотность источников теплоты, Вт/м³;

с – теплоемкость, Дж/(кг×К);

r – плотность, кг/м³.

Решение уравнения (2.19) в учебниках по теплотехнике [32] приводится методами математической физики. Наиболее простой способ решения этого уравнения – случай одномерной нестационарной теплопроводности без внутренних источников теплоты, следовательно, выражение (2.19) преобразуем в:

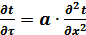. (2.20)

Для решения уравнения (2.20), как правило, используют метод разделения переменных. В этом случае, температуру t представляют в виде произведения двух функций:

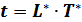, (2.21)

где L^*=f(x) зависит только от x, а T^*=f(τ) зависит только от τ.

Следовательно:

; ; .

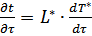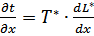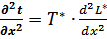Подставляя эти значения в выражение (2.20) получим:

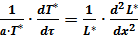. (2.22)

Левая часть уравнения (2.22) является функцией времени, т.е. только τ, а правая функция геометрического размера по оси x. Эти функции могут быть равны лишь в том случае, когда они являются постоянной величиной. В любом другом случае, т.к. τ и x независимые аргументы, равенства быть не может:

.

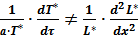Если обозначим эту функцию как –β², то получим:

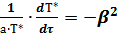; (2.23)

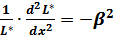. (2.24)

Решение уравнения (2.23) примет вид:

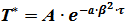. (2.25)

Знак минус у величины β² соответствует условиям охлаждения, которые можно применить для телиц, так как в течение времени, τ несомненно, будет падение температуры t.

Решение уравнения (2.24) в нашем случае, т.е. если по оси x теплица ограничена неограниченной плоской пластиной, имеющей начальную температуру t_д и помещенную в момент времени τ=0 в среду с температурой t_нв имеет вид:

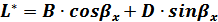. (2.26)

На границах пластины происходит теплообмен по закону Ньютона. Т.к. задача симметрична, то примем толщину пластины 2δ и поместим ось х в центре пластины (рисунок 2.4).

В силу симметричности функции cos запишем выражение (2.26) в виде L^*=B×cosβ_x и уравнение поля температур t=L^*×T^*:

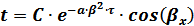. (2.27)

Вводя критерии подобия:

, , ,

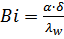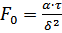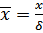получим:

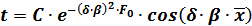, (2.28)

где величина d×β=μ^* может быть найдена из характеристического уравнения:

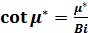. (2.29)

Уравнение (2.29) решается графическим путем, и имеет бесчисленное множество корней 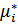и приводится в нескольких изданиях, посвященных теоретической теплотехнике и математике [32, 52].

Сумма частных решений дает общее в следующем виде:

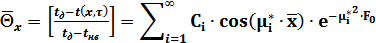(2.30)

Значения постоянных C_i определяют из начальных условий (τ=0; t_д=t₀):

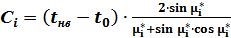. (2.31)

Подставляя значения постоянных C_i в уравнение (2.32), можем получить окончательное выражение для поля температур по оси х:

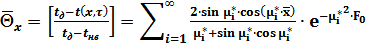(2.32)

Будет целесообразно теплицу в сечении по оси х представить, как неограниченную пластину с граничными условиями третьего рода (рисунок 2.6).

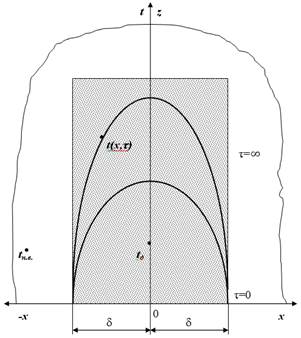
Рисунок 2.6 Нестационарное температурное поле

Ряд, для определения температурного поля по оси х, является сходящимся. Это значит, что с определенного значения 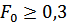все последующие члены ряда по сравнению с первым ничтожно малы. Следовательно, при 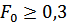можно ограничиться только первым членом ряда, тогда мы получим:

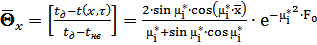. (2.33)

В конкретной точке пластины, а, следовательно, и теплицы по оси х, ее температура зависит только от критериев подобия, принятым выше, Bi и F₀.

Поскольку, внутреннее термическое сопротивление теплицы по сравнению с внешним термическим сопротивлением окружающей среды велико, т.е. 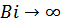, то в этой задаче, граничные условия третьего рода переходят в граничные условия первого рода. При этих условиях ( 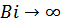и 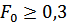) из уравнения (2.33) получим ():

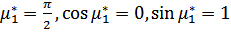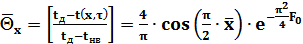(2.34)

Проводя аналогичные вычисления, температурное поле в теплице по оси y можно представить как:

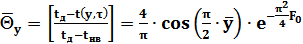(2.35)

По оси z температурное поле можно описать аналогично процессам нагрева в половине цилиндра, т.е. аналитическим выражением (2.36):

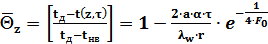, (2.37)

где а – коэффициент изобарной температуропроводности, для воздуха

составляет 18,88×10⁶ ;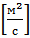

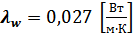– коэффициент теплопроводности воздуха;

a – коэффициент конвективной отдачи для воздуха равен 500 ;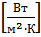

τ – текущий момент времени, с;

r – радиус цилиндра, равный высоте z от поверхности земли до точки в

которой необходимо определить температуру.

Далее можно от безразмерных величин температурного поля перейти к конкретным значениям температуры в какой-либо точке рабочего объема защищенного грунта. Используя выражение (2.18):

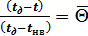(2.37)

Умножая и левую и правую части выражения (2.37) на 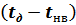получим:

.

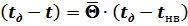Следовательно, t равно:

.

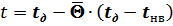Учитывая, что 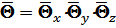, получим:

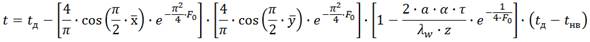(2.38)

Проведя ряд математических преобразований, принимая, что радиус r, вписанного в теплицу цилиндра, равен высоте по координате z (рисунок 2.7), а также переводя относительные величины 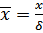и 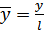в реальные, где l – длина теплицы, м. Из выражения (2.38) получим:

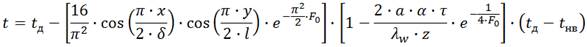(2.39)

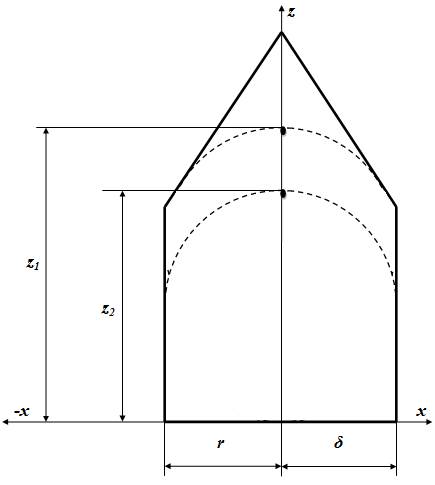
Рисунок 2.7 Поперечное сечение теплицы

Задача лабораторной работы:

Создать в ПК CoDeSys систему управления, использующая модель, представленную выражением (2.39), при успешном доказательстве её адекватности, позволяющую решать следующие задачи:

· Учитывать температуру в любой точке рабочего объема защищенного грунта, получая данные лишь с датчика, установленного в геометрическом центре теплицы t _д;

· Работать во взаимосвязанном режиме с учетом освещенности биологических объектов в теплице. При этом выполнять функции энергосбережения, закрывая экран зашторивания;

· Принимать решения о повышении температуры в теплицы для удаления чрезмерного снежного покрова на коньках теплицы, снижающего освещенность биологических объектов ниже допустимого.