Теоретическая часть. При проведении ряда повторных независимых испытаний событие А может появиться с некоторой вероятностью р и не появиться с вероятностью 1-р=q

Лабораторная работа № 3

«Формула Бернулли».

Теоретическая часть.

При проведении ряда повторных независимых испытаний событие А может появиться с некоторой вероятностью р и не появиться с вероятностью 1-р=q. Ставится задача определить вероятность того, что в n испытаниях событие А появится ровно m раз. Искомая вероятность определяется отношением:

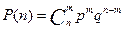
Данная формула является единственной точной формулой в схеме независимых повторных испытаний. Однако, использовать ее можно в ограниченных условиях (n≤15, р отлично от 0 и 1). Поэтому, на практике часто используют приближенные формулы:

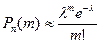– формула Пуассона, где λ=np.

Исходя из условия, формулу Пуассона удобно применять при n→∞, p→0. Если же р существенно отличается от нуля, то λ становится значительным по величине и применение формулы становится затруднительным. В этом случае используется локальная теорема Муавра-Лапласа:

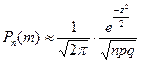, где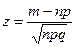

При большом числе испытаний наибольшей интерес представляют вероятности того, что число m появления события А заключено в некотором интервале от m₁ до m₂. Решение этого вопроса связано с интегральной теоремой Муавра- Лапласа:

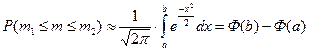, где ,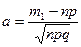

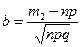
Если npq сравнительно невелико, то лучшее приближение дает формула

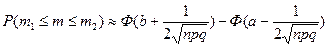, где ,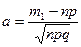

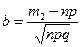
Интегральная теорема Муавра- Лапласа позволяет найти вероятность того, что отклонение относительной частоты появления некоторого события m/n от постоянной вероятности по абсолютной величине не превысит заданного положительного числа ε:

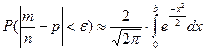, где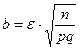

Можно определить количество испытаний необходимых для того, чтобы отклонение относительной частоты успехов 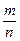от вероятности р было меньше ε с вероятностью большей или равной β, то есть найти n, для которого выполняется неравенство:

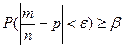
Доказано, что число n обеспечивает выполнение этого неравенства, если оно удовлетворяет соотношению

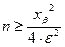, где х_β –решение уравнения Ф(х_β)=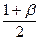

Если вероятность р известна, то необходимое число испытаний определяется формулой

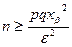, значение корня уравнения Ф(х_β)=а дает функция qnorm(a,0,1).

Для вычисления значений функции Лапласа Ф(х) предназначена функция pnorm(x,0,1).

Список некоторых распределений, представленных в библиотеке MathCad, и миена соответствующих функций (Имена всех встроенных функций, начинающихся с буквы d определяют плотности вероятностей, с буквы p – функции распределения, с q - квантили):

биномиальное распределение – dbinom(k,n,p), pbinom(k,n,p), qbinom(k,n,p);

нормальное распределение – dnorm(x,μ,σ), pnorm(x,μ,σ), qnorm(x,μ,σ);

распределение Пуассона – dpois(x,λ), pnorm(x,μ,σ), qnorm(x,μ,σ).