РОСЖЕЛДОР
Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«Ростовский государственный университет путей сообщения»
(ФГБОУ ВПО РГУПС)
 В.М. Павлов
В.М. Павлов
РАСЧЕТ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ В ВОЛНОВОДЕ
Учебно-методическое пособие
для выполнения курсовой работы
Ростов-на-Дону
УДК 621.372.8 (07)+06
Павлов, В.М.
Расчет электромагнитного поля в волноводе: учебно-методическое пособие для выполнения курсовой работы / В.М. Павлов; Рост. гос. ун-т путей сообщения. – Ростов н/Д, 2012. - 33 с.: ил.
Учебно-методическое пособие содержит теоретические сведения и методические указания для выполнения курсовой работы «Расчет электромагнитного поля в волноводе» по дисциплине «Электромагнитные поля и волны».
Предназначено для студентов факультета «Автоматика, телемеханика и связь» РГУПС.
Рецензент канд. техн. наук, доц. В.И. Юхнов (РГУПС)
© Ростовский государственный университет
путей сообщения, 2012
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ..................................................................................................................4
1 КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ.....................................................................5
1.1 Прямоугольный волновод..........................................................................5
1.2 Поперечно-электрические поля….............................................................8
1.3 Поперечно-магнитные поля.....................................................................12
1.4 Поверхностные токи в волноводе…........................................................13
2 ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ................................................................17
3 МЕТОДИЧЕСКИЕ УКАЗАНИЯ...........................................................................18
4 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.............................................21
Приложение А Некоторые сведения из векторного анализа................................22
Приложение Б Структура электромагнитных полей.............................................24
Приложение В Варианты заданий и исходные данные.........................................26
Приложение Г Образец оформления титульного листа........................................30
Приложение Д Образец оформления задания........................................................31
ВВЕДЕНИЕ
Направляющими системами в электродинамике называются технические устройства, которые принудительно направляют (канализируют) поток энергии переменного электромагнитного поля в нужном направлении (например, от передатчика к антенне или от антенны к приемнику). В начале развития радиотехники, которая за время своего существования продвинулась в направлении возрастания практически используемых частот от 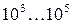 Гц до
Гц до 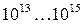 Гц, направляющие системы были представлены открытыми двух -, трех -, четырех - проводными линиями, широко применяемыми и в настоящее время.
Гц, направляющие системы были представлены открытыми двух -, трех -, четырех - проводными линиями, широко применяемыми и в настоящее время.
При повышении частоты многопроводные линии, будучи открытыми, перестали справляться с возложенной на них задачей: передачей энергии электромагнитного поля с малыми потерями.
На коротких волнах, сравнимых с размерами открытой линии, последние заметную часть энергии начинают излучать в поперечном направлении. С укорочением длины волны приходится уменьшать поперечные размеры линии (только при этом условии она нормально работает как устройство передачи - длинная линия). Поперечное излучение эффективно устраняется введением экрана.
Однако, в высокочастотной радиоэлектронике такие линии не нашли широкого применения: конструкция их сложна, вдобавок трудно поддержать постоянным на большой длине линии соотношение поперечных размеров и форму сечения. Тем не менее, двухпроводные линии и сегодня еще применяются для передачи энергии электромагнитных волн длиной вплоть до метрового диапазона. На дециметровых волнах двухпроводные линии пришлось полностью заменить коаксиальными линиями передачи.
В коаксиальной линии вся энергия передается в пространстве между центральным и внешним проводниками, и потери на излучение в поперечном направлении исключены. Однако по мере приближения к сантиметровым волнам и в коаксиальной линии стали проявляться недостатки: с ростом частоты, то есть с укорочением длины волны, приходится пропорционально уменьшать поперечные размеры линии, при этом выдержать постоянными радиусы внутреннего и внешнего проводников, их соосность становится трудно. Возникающие неизбежные отклонения поперечных размеров нарушают нормальный режим распространения волн в такой линии.
Другой недостаток связан с опасностью электрического пробоя, который возникает в месте высокой концентрации электрического поля у поверхности внутреннего проводника. Плотность тока, протекающего по поверхности внутреннего проводника, больше, чем по поверхности внешнего. Поэтому потери коаксиальной линии, связанные со скин-эффектом, в наибольшей степени вызваны наличием именно внутреннего проводника.
В сантиметровом диапазоне волн на смену коаксиальным линиям пришли полые металлические трубы, в которых внутренний проводник удален.
Полые металлические волноводы перекрывают весь сантиметровый и длинноволновую часть миллиметрового диапазонов.
1 КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1.1 Прямоугольный волновод
В диапазоне сверхвысоких частот (СВЧ) широко применяются радиоволноводы или просто - волноводы. Волновод представляет собой полую металлическую трубу, в которой при определенных условиях могут распространяться электромагнитные волны.
Для определения поля в полом волноводе в общем случае необходимо решить систему уравнений Максвелла или соответствующих им волновых уравнений. При этом решение ищут в той системе координат, координатные поверхности которой по форме подобны внутренней поверхности волновода, т.е. решение уравнений Максвелла для прямоугольного волновода ищут в прямоугольной системе координат, для круглого - в цилиндрической. Постоянные интегрирования находят исходя из требования, чтобы полученные решения удовлетворяли граничным условиям на внутренней поверхности волновода.
Рассмотрим свойства наиболее распространенного типа волноводов: прямоугольного (рисунок 1) [1,2].
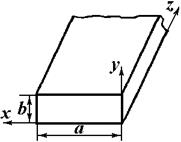
Рис. 1. Прямоугольный волновод
Для исследования структуры электромагнитного поля в волноводе, необходимо решить уравнения Максвелла в комплексной форме
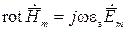 ,
,
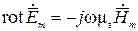 , (1)
, (1)
в области
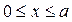 ;
; 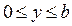 ;
; 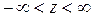 (2)
(2)
при заданных граничных условиях на проводящих стенках волновода:
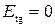 при
при 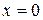 ;
; 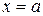 ;
; 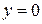 ;
; 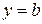 ;
; 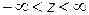 . (3)
. (3)
В выражениях (1) и далее 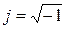 - мнимая единица.
- мнимая единица.
В дальнейших выражениях индекс " 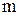 " у комплексных амплитуд опустим.
" у комплексных амплитуд опустим.
Параметры среды, заполняющей внутреннее пространство волновода 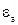 ,
, 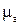 ,
, 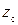 ,
,
где 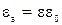 – абсолютная диэлектрическая проницаемость среды, Ф/м;
– абсолютная диэлектрическая проницаемость среды, Ф/м;
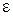 – относительная диэлектрическая проницаемость среды;
– относительная диэлектрическая проницаемость среды;
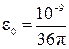 – абсолютная диэлектрическая проницаемость вакуума, Ф/м;
– абсолютная диэлектрическая проницаемость вакуума, Ф/м;
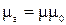 – абсолютная магнитная проницаемость среды, Гн/м;
– абсолютная магнитная проницаемость среды, Гн/м;
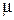 – относительная магнитная проницаемость среды;
– относительная магнитная проницаемость среды;
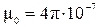 – абсолютная магнитная проницаемость вакуума, Гн/м;
– абсолютная магнитная проницаемость вакуума, Гн/м;
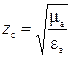 – волновое сопротивление среды, Ом.
– волновое сопротивление среды, Ом.
Будем считать, что волновод имеет большую протяженность, и что источники поля в рассматриваемой области отсутствуют. Нас будут интересовать условия, при которых решение уравнений поля имеет форму бегущей волны, распространяющейся вдоль оси волновода в направлении возрастающих значений 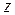 . Поэтому положим, что зависимость всех составляющих поля
. Поэтому положим, что зависимость всех составляющих поля 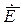 и
и 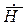 от координаты
от координаты 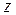 имеет вид
имеет вид
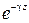 , (4)
, (4)
где 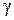 - постоянная распространения, которая должна быть найдена в результате решения уравнений Максвелла при граничных условиях (3).
- постоянная распространения, которая должна быть найдена в результате решения уравнений Максвелла при граничных условиях (3).
Условие (4) означает, что дифференцирование комплексных амплитуд любой из проекций вектора 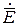 или
или 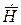 по переменной
по переменной 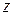 эквивалентно умножению этой проекции на
эквивалентно умножению этой проекции на 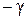 , т.е. оператор
, т.е. оператор 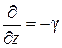 .
.
Из уравнений Максвелла (1) в декартовой системе координат (приложение А) для внутреннего пространства волновода получим:
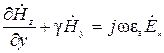 , (5)
, (5)
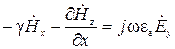 , (6)
, (6)
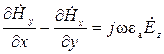 , (7)
, (7)
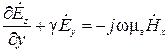 , (8)
, (8)
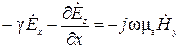 , (9)
, (9)
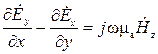 . (10)
. (10)
Проведем преобразование системы уравнений (5) - (10) так, чтобы выразить поперечные составляющие векторов (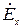 ,
, 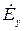 ,
, 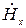 ,
, 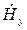 ) через продольные
) через продольные 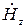 и
и 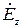 . Для этого в уравнения (5) и (6) подставим значения
. Для этого в уравнения (5) и (6) подставим значения 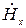 и
и 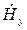 из уравнений (8) и (9) и после простых преобразований получим:
из уравнений (8) и (9) и после простых преобразований получим:
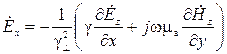 , (11)
, (11)
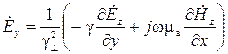 , (12)
, (12)
где 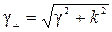 – поперечное волновое число;
– поперечное волновое число;
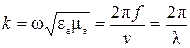 , – волновое число;
, – волновое число;
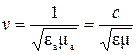 – скорость волны в среде, заполняющей волновод;
– скорость волны в среде, заполняющей волновод;
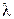 – длина волны в этой среде.
– длина волны в этой среде.
Теперь, подставляя в уравнения (8) и (9) значения 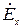 , и
, и 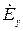 из уравнений (5) и (6), получим уравнения для составляющих
из уравнений (5) и (6), получим уравнения для составляющих 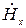 и
и 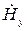 , выраженных через величины
, выраженных через величины 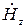 и
и 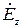 .
.
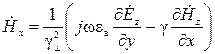 , (13)
, (13)
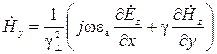 . (14)
. (14)
Таким образом, все составляющие векторов 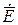 и
и 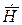 , касательные к плоскости поперечного сечения (поперечные составляющие), определяются через продольные составляющие
, касательные к плоскости поперечного сечения (поперечные составляющие), определяются через продольные составляющие 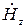 и
и 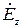 . Уравнения для продольных составляющих легко получить, подставляя значения
. Уравнения для продольных составляющих легко получить, подставляя значения 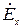 и
и 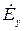 из (11) и (12) в уравнение (10), а значения
из (11) и (12) в уравнение (10), а значения 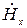 и
и 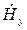 из (13) и (14) в уравнение (7), тогда
из (13) и (14) в уравнение (7), тогда
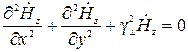 , (15)
, (15)
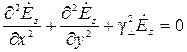 . (16)
. (16)
Это волновые уравнения [3].
Из выражений (11) … (14) следует, что электромагнитное поле в прямоугольном волноводе в общем случае представляет собой сумму двух независимых частных полей, одно из которых называется поперечно-электрическим (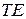 -полем или
-полем или 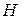 -полем).
-полем).
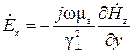 ;
; 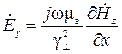 ;
; 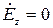 , (17)
, (17)
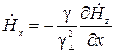 ;
; 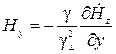 ;
; 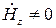 , (18)
, (18)
так как не содержит продольных составляющих электрического поля(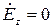 ).
).
Второе получило название поперечно-магнитное (или 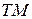 -поле,
-поле, 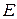 -поле)
-поле)
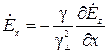 ;
; 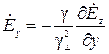 ;
; 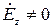 , (19)
, (19)
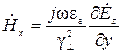 ;
; 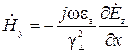 ;
; 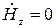 . (20)
. (20)
так как не содержит продольных составляющих магнитного поля (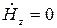 ).
).
Перейдем к рассмотрению каждого из этих полей.
1.2 Поперечно-электрические поля
Чтобы определить типы электромагнитных волн в прямоугольном волноводе и проанализировать структуру электромагнитных полей, необходимо решить уравнение (15) при общих граничных условиях (3). Применительно к поперечно-электрическому полю (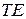 или
или 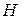 ) граничные условия имеют вид
) граничные условия имеют вид
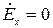 при
при 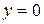 ;
; 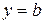 ;
;
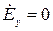 при
при 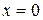 ;
; 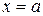 . (21)
. (21)
Используя выражения (17), при условии (21) получаем
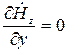 при
при 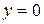 ;
; 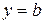 ;
;
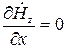 при
при 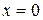 ;
; 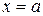 . (22)
. (22)
Напомним, что для 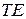 - или
- или 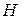 -поля
-поля 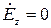 .
.
Решение волнового уравнения (15) осуществляется методом разделения переменных. Будем искать решение в виде
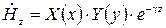 , (23)
, (23)
где 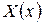 и
и 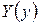 - функции, зависящие только от
- функции, зависящие только от 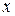 и
и 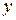 соответственно. Подставляя последние выражения в уравнение (15), получим,
соответственно. Подставляя последние выражения в уравнение (15), получим,
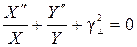 ,
,
откуда следует, что
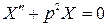 и
и 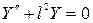 ; (24)
; (24)
где 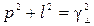 ;
;
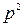 и
и 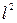 – произвольные постоянные разделения.
– произвольные постоянные разделения.
Как известно, общее решение уравнений (24), можно представить следующим образом:
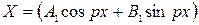 ,
,
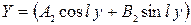 .
.
Следовательно, в соответствии с (23) проекция 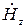 будет равна
будет равна
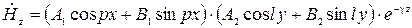 , (25)
, (25)
причем постоянная распространения в соответствии с (12) и (24) определяется как
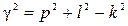 .
.
Чтобы найти входящие в выражение для 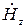 неизвестные величины, воспользуемся граничными условиями (22). Из первого условия вытекает, что
неизвестные величины, воспользуемся граничными условиями (22). Из первого условия вытекает, что
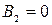 ;
; 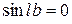 ;
; 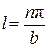 ;
; 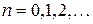 .
.
Из второго условия получается:
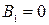 ;
; 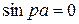 ;
; 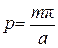 ;
; 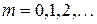 .
.
Таким образом,
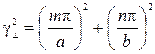 , (26)
, (26)
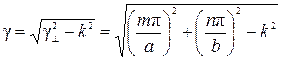 , (27)
, (27)
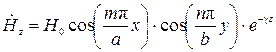 . (28)
. (28)
Здесь введено обозначение 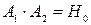 .
.
Подставив значение 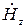 в равенства (17) и (18), получим выражения для комплексных амплитуд остальных составляющих векторов электромагнитного поля в прямоугольном волноводе для поперечно-электрических волн
в равенства (17) и (18), получим выражения для комплексных амплитуд остальных составляющих векторов электромагнитного поля в прямоугольном волноводе для поперечно-электрических волн 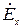 ,
, 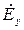 ,
, 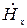 и
и 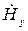 .
.
Отметим, что при 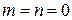 волны в волноводе существовать не могут, так как в этом случае все компоненты поля, за исключением
волны в волноводе существовать не могут, так как в этом случае все компоненты поля, за исключением 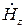 , обращаются в нуль. Из этого следует, что числа
, обращаются в нуль. Из этого следует, что числа 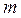 и
и 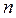 могут принимать любые значения, равные 0,1,2,3,..., но не могут быть одновременно равными нулю.
могут принимать любые значения, равные 0,1,2,3,..., но не могут быть одновременно равными нулю.
Следовательно, в прямоугольном волноводе могут существовать бесчисленное множество типов поперечно-электрических волн, определяемых значениями чисел 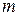 и
и 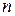 . Эти волны обозначаются символами
. Эти волны обозначаются символами 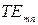 (или
(или 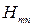 ). В общем случае компоненты поля записываются в виде суммы различных типов волн по индексам
). В общем случае компоненты поля записываются в виде суммы различных типов волн по индексам 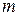 и
и 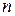 .
.
Вдоль сторон 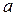 и
и 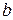 поперечного сечения волновода распределение поля имеет характер стоячей волны, причем величина
поперечного сечения волновода распределение поля имеет характер стоячей волны, причем величина 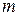 определяет число полуволн стоячей волны, укладывающихся вдоль оси
определяет число полуволн стоячей волны, укладывающихся вдоль оси 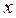 на интервале
на интервале 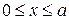 , а
, а 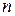 - число полуволн стоячей волны вдоль оси
- число полуволн стоячей волны вдоль оси 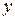 на интервале
на интервале 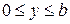 .
.
Поле будет распространяться вдоль оси 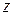 в виде бегущей волны, если постоянная распространения
в виде бегущей волны, если постоянная распространения 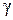 равна чисто мнимой величине
равна чисто мнимой величине
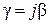 , (29)
, (29)
где 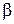 - фазовая постоянная (продольное волновое число волновода).
- фазовая постоянная (продольное волновое число волновода).
В противном случае поле в волноводе быстро уменьшается с расстоянием 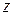 вследствие экспоненциального множителя
вследствие экспоненциального множителя 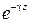 .
.
Из выражений (27) и (29) следует, что
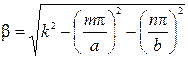 . (30)
. (30)
С учетом сказанного продольная составляющая магнитного поля (28) примет вид
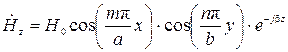 . (31)
. (31)
Из равенства (30) следует, что в прямоугольном волноводе поперечно-электрическая волна (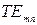 ) при данных размерах
) при данных размерах 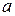 и
и 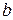 будет незатухающей, если
будет незатухающей, если
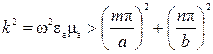 .
.
Отсюда следует неравенство
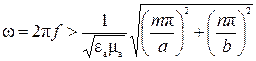 ,
,
или
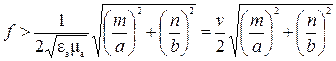 .
.
Величина
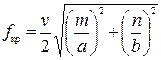 (32)
(32)
имеет размерность 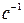 и носит название критической частоты волновода.
и носит название критической частоты волновода.
Критической частоте соответствует критическая длина волны, которая определяется формулой
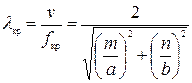 , (33)
, (33)
Таким образом, условие распространения волны по волноводу имеет вид
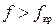 или
или 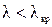 . (34)
. (34)
Фазовая скорость 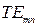 -волны определяется по формуле
-волны определяется по формуле
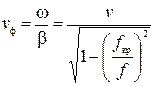 , (35)
, (35)
а скорость переноса энергии равна
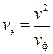 . (36)
. (36)
Длина волны в волноводе определяется выражением
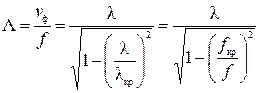 . (37)
. (37)
Из выражения (37) для длины волны в волноводе следует, что она отличается от длины волны в свободном пространстве и от длины волны в среде, заполняющей волновод.
Из выражения для фазовой скорости (35) видно, что волновод является дисперсной средой, так как фазовая скорость, а, следовательно, и скорость переноса энергии, зависит от частоты колебаний источника радиоволн.
При решении задач теории волноводов, кроме понятия волнового сопротивления среды 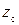 , заполняющей волновод, пользуются понятием характеристического сопротивления волновода
, заполняющей волновод, пользуются понятием характеристического сопротивления волновода 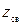 . Характеристическое сопротивление в случае
. Характеристическое сопротивление в случае 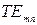 волн определяется в виде
волн определяется в виде
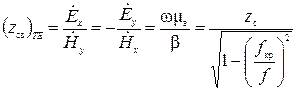 . (38)
. (38)
Из выражения (32) следует, что при одинаковых размерах поперечного сечения волновода критическая частота растет с увеличением 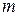 и
и 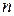 , т.е. высшие типы поперечно-электрических волк (с большими значениями
, т.е. высшие типы поперечно-электрических волк (с большими значениями 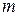 и
и 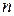 ) имеют более высокие критические частоты по сравнению с низшими типами. Следовательно, для передачи электромагнитной энергии при заданной частоте источника колебаний по волноводу с наименьшими поперечными размерами необходимо возбуждать в нем волну с наименьшими значениями
) имеют более высокие критические частоты по сравнению с низшими типами. Следовательно, для передачи электромагнитной энергии при заданной частоте источника колебаний по волноводу с наименьшими поперечными размерами необходимо возбуждать в нем волну с наименьшими значениями 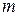 и
и 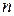 . При размере
. При размере 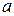 большем
большем 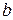 это будет волна
это будет волна 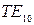 (или
(или 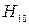 ). Этот тип волны, называемый основным типом волны в прямоугольном волноводе, находит наибольшее применение на практике.
). Этот тип волны, называемый основным типом волны в прямоугольном волноводе, находит наибольшее применение на практике.
Мощность, передаваемая через поперечное сечение волновода волной 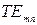 по определению равна
по определению равна
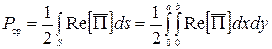 , (39)
, (39)
где 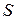 – поперечное сечение волновода;
– поперечное сечение волновода;
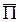 – продольная составляющая вектора Пойнтинга [1,2].
– продольная составляющая вектора Пойнтинга [1,2].
Для прямоугольного волновода эта величина равна 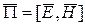 , следовательно (приложение А)
, следовательно (приложение А)
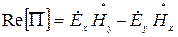 , (40)
, (40)
где 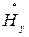 и
и 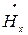 – величины, комплексно-сопряженные составляющим
– величины, комплексно-сопряженные составляющим 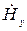 и
и 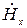 соответственно.
соответственно.
Следует отметить, что правая часть выражения (39) справедлива лишь для волновода прямоугольного сечения.
 2015-05-13
2015-05-13 1088
1088








