|
Определение. Отображение  называется гомоморфизмом, если называется гомоморфизмом, если 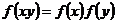 . Инъективный гомоморфизм называется мономорфизмом. Сюръективный гомоморфизм называется эпиморфизмом. Биективный гомоморфизм называется изоморфизмом. Изоморфизм группы на себя называется автоморфизмом. . Инъективный гомоморфизм называется мономорфизмом. Сюръективный гомоморфизм называется эпиморфизмом. Биективный гомоморфизм называется изоморфизмом. Изоморфизм группы на себя называется автоморфизмом.
Примеры:
1) 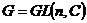 , ,  . .  - гомоморфизм. - гомоморфизм.
2) 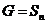 , ,  . .  - гоморфизм. - гоморфизм.
3) 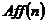 - группу аффинных преобразования - группу аффинных преобразования 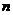 -мерного пространства отобразим на -мерного пространства отобразим на  - группу линейных преобразований - группу линейных преобразований 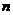 -мерного пространства. Будем ставить аффинному преобразованию в соответствие его дифференциал, т.е. -мерного пространства. Будем ставить аффинному преобразованию в соответствие его дифференциал, т.е. 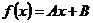 - аффинное преобразование перейдет в - аффинное преобразование перейдет в 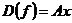 . Это будет гомоморфизмом. . Это будет гомоморфизмом.
4) Пусть есть группа  , возьмем элемент , возьмем элемент 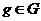 . Автоморфизм сопряжения с помощью элемента . Автоморфизм сопряжения с помощью элемента 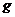 : : 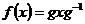 . Этот автоморфизм нетривиален (не тождественный), если найдется . Этот автоморфизм нетривиален (не тождественный), если найдется 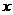 такой, что такой, что 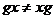 . .
Определение. Группа называется абелевой (коммутативной), если 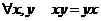 . .
Предложение. Если 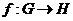 - гомоморфизм, то - гомоморфизм, то 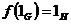 и и  . .
Здесь  - единичный элемент группы - единичный элемент группы 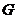 , , 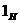 - единичный элемент группы - единичный элемент группы 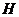 . .  - обратный к - обратный к  элемент группы элемент группы 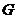 , ,  - обратный к - обратный к  элемент группы элемент группы 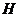 . .
Доказательство.
1) Т.к.  , то , то  . Имеем . Имеем
 . .
2) 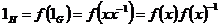 , следовательно , следовательно 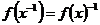 . . 
Предложение. Гомоморфизм 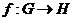 является мономорфизмом тогда и только тогда, когда из является мономорфизмом тогда и только тогда, когда из 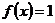 следует следует  , т.е. полный прообраз единицы равен единице. , т.е. полный прообраз единицы равен единице.
Доказательство.
 Если Если  мономорфизм и мономорфизм и 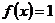 . Т.к. . Т.к.  и и  инъективно, то инъективно, то 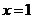 . .
 Пусть Пусть 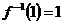 (полный прообраз) и (полный прообраз) и 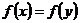 . Тогда . Тогда
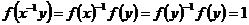 . По условию . По условию 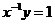 , т.е. , т.е.  . Следовательно . Следовательно 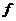 - инъективно, т.е. является мономорфизмом. - инъективно, т.е. является мономорфизмом. 
Определение. Пусть отображение 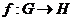 - гомоморфизм групп. Тогда ядром этого отображения называется множество - гомоморфизм групп. Тогда ядром этого отображения называется множество  , т.е. полный прообраз единицы. , т.е. полный прообраз единицы.
По предыдущему предложению получаем, что 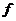 - мономорфизм тогда и только тогда, когда - мономорфизм тогда и только тогда, когда 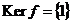 . .
Упражнение. Пусть  - гомоморфизм групп, доказать, что - гомоморфизм групп, доказать, что  является подгруппой в является подгруппой в 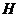 . .
Определение. Подгруппа  в группе в группе  называется нормальной (обозначается называется нормальной (обозначается  ), если ), если 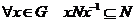 , т.е. если , т.е. если  . .
Предложение. Пусть 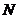 - подгруппа в - подгруппа в 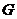 , тогда следующие утверждения эквивалентны: , тогда следующие утверждения эквивалентны:
1) 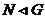 ; ;
2)  ; ;
3) каждый правый смежный класс совпадает с левым, т.е.  . .
Доказательство.
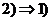 Очевидно. Очевидно.
 Надо доказать, что Надо доказать, что  , пусть , пусть 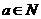 , тогда , тогда 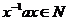 . Поэтому . Поэтому 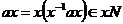 , следовательно , следовательно  . Обратно аналогично: . Обратно аналогично: 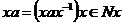 , следовательно , следовательно 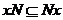 и и 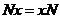 . .
 Мы имеем, что Мы имеем, что  . Возьмем произвольный элемент . Возьмем произвольный элемент 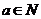 , тогда , тогда 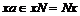 , т.е. , т.е.  , но тогда , но тогда  . Мы получили, что . Мы получили, что  . Теперь покажем, что таким образом можно получить любой элемент из . Теперь покажем, что таким образом можно получить любой элемент из  , т.е. что , т.е. что  . Если . Если 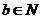 , то , то  , следовательно , следовательно 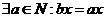 , но тогда , но тогда 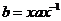 . Следовательно . Следовательно 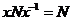 . . 
Пример:
При помощи этого предложения можно доказать, что  не является нормальной подгруппой в не является нормальной подгруппой в 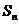 , т.к. ее левые и правые смежные классы не совпадают. , т.к. ее левые и правые смежные классы не совпадают.
Теорема. Пусть 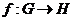 - гомоморфизм, тогда - гомоморфизм, тогда  . .
Доказательство.
Сначала докажем, что 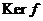 является подгруппой в является подгруппой в  . .
Если  , то и , то и 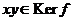 , т.к. , т.к. 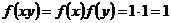 . .
Если 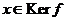 , то и , то и 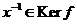 , т.к. , т.к. 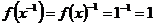 . .
Теперь докажем нормальность этой подгруппы.
 , следовательно , следовательно 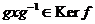 и и 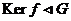 . . 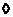
Примеры:
1)  , ,  . Тогда . Тогда  . .
2) 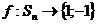 , ,  . Тогда . Тогда 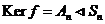 . .
3) 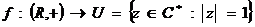 , , 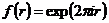 . Тогда . Тогда 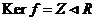 . .
Предложение. Если  - гомоморфизм и - гомоморфизм и 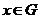 , тогда , тогда 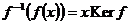 . .
Доказательство.
 . . 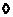
Определение. Пусть  , фактор группа , фактор группа 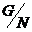 - это множество смежных классов - это множество смежных классов 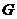 по по 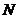 с операцией с операцией 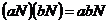 . .
Теорема.  - группа. - группа.
Доказательство.
Сначала докажем, что операция определена корректно. Пусть 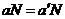 и и 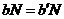 , покажем, что , покажем, что  . Имеем . Имеем  и и 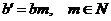 , тогда , тогда  . Причем . Причем 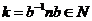 , следовательно , следовательно 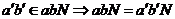 . .
Ассоциативность операции: 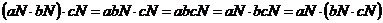 . .
Единичный элемент: 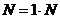 . .
Обратный элемент:  . . 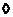
Отображение 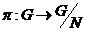 , ,  называется естественным эпиморфизмом. называется естественным эпиморфизмом.
Теорема. Отображение - эпиморфизм и - эпиморфизм и 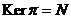 . .
Доказательство.
 , т.к. , т.к.  , то у любого смежного класса есть прообраз, следовательно, это эпиморфизм. Т.к. , то у любого смежного класса есть прообраз, следовательно, это эпиморфизм. Т.к. 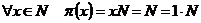 , то , то  . . 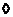
Теорема (о гомоморфизме). Пусть  - гомоморфизм групп, тогда - гомоморфизм групп, тогда  (изоморфно). (изоморфно).
Доказательство.
Построим изоморфизм  : : 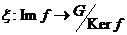 , , 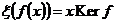 . Эта отображение определено корректно, т.к. . Эта отображение определено корректно, т.к.  . .
Докажем, что это гомоморфизм:
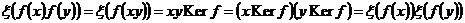 . .
Докажем биективность, т.е. что это изоморфизм. Т.к. 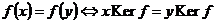 , это отображение биективно. , это отображение биективно. 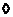
Пример:
Покажем, как при помощи этой теоремы доказать изоморфность  . Нам нужно задать гомоморфизм . Нам нужно задать гомоморфизм  такой, чтобы такой, чтобы 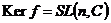 . Например . Например  . Тогда по теореме о гомоморфизме будем иметь, что . Тогда по теореме о гомоморфизме будем иметь, что 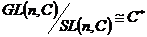 . .
Лекция 3 (17.09.2001)
Теорема. Циклическая группа порядка  изоморфна группе изоморфна группе 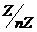 . .
Доказательство.
Пусть  . Зададим гомоморфизм . Зададим гомоморфизм  следующим образом: следующим образом:  . Это гомоморфизм, т.к. . Это гомоморфизм, т.к.  . Тогда по теореме о гомоморфизме имеем . Тогда по теореме о гомоморфизме имеем 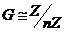 . . 
Упражнение. Бесконечная циклическая группа изоморфна группе  . .
Определение. Пусть  - группа. - группа.  - произвольное множество. - произвольное множество. 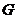 действует на действует на  , если есть отображение , если есть отображение 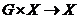 , т.е. которое паре , т.е. которое паре 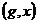 ставит в соответствие некоторый элемент ставит в соответствие некоторый элемент 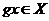 . Причем . Причем 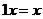 и и 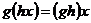 . .
Примеры:
1) 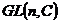 действует на действует на 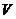 - -  -мерном комплексном пространстве, по следующему правилу: пусть -мерном комплексном пространстве, по следующему правилу: пусть 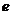 - базис, в нем вектор - базис, в нем вектор  имеет координаты имеет координаты  , тогда , тогда 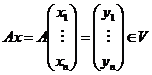 . .
2) Пусть  - подгруппа в - подгруппа в  , тогда , тогда  действует на действует на 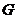 по правилу по правилу 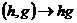 . .
3) Пусть  и и 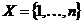 . Имеем естественное действие симметрической группы на множестве . Имеем естественное действие симметрической группы на множестве  . .
4) Пусть 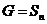 и и 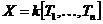 - многочлены от - многочлены от  неизвестных. Действие определим по правилу неизвестных. Действие определим по правилу 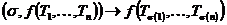 . .
5)  действует на действует на  сопряжением сопряжением 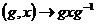 . Т.к. . Т.к. 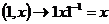 и и  , то это действительно будет действием. , то это действительно будет действием.
Предложение. Пусть 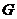 действует на действует на 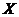 и и 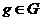 , тогда отображение , тогда отображение 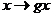 является биекцией на множестве является биекцией на множестве 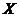 . .
Доказательство.
Для доказательства этого факта на достаточно указать обратное отображение. Им будет отображение 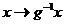 . Оно действительно будет обратным, т.к. . Оно действительно будет обратным, т.к.  и и  . Следовательно, это биекция. . Следовательно, это биекция. 
Определение. Пусть  действует на действует на 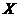 и и  . Орбита . Орбита 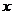 - это множество - это множество 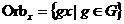 . Стабилизатор . Стабилизатор  - это множество - это множество 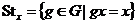 . .
Упражнение. Доказать, что 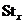 является подгруппой в является подгруппой в 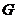 . .
Определение. Пусть  - группа - группа 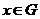 . Централизатор . Централизатор  - это множество - это множество 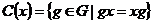 . Класс сопряженных элементов, содержащий . Класс сопряженных элементов, содержащий 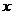 - это множество - это множество  . .
Примеры:
1) При действии  на на  - - 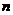 -мерном пространстве будет всего две различные орбиты: все ненулевые векторы (орбита любого ненулевого вектора), ноль (орбита нуля). -мерном пространстве будет всего две различные орбиты: все ненулевые векторы (орбита любого ненулевого вектора), ноль (орбита нуля).
2) При действии подгруппы 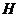 на группе на группе 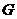 имеем имеем 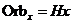 и и 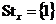 . .
3) При действии  на себе сопряжением имеем на себе сопряжением имеем 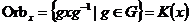 , ,  . .
Предложение. Если орбиты пересекаются, то они совпадают.
Доказательство.
Пусть 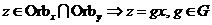 . . 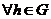 имеем имеем 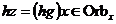 , следовательно , следовательно 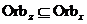 . .  имеем имеем 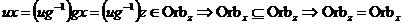 . Аналогично имеем . Аналогично имеем  . . 
Предложение.  . .
Доказательство.
Допустим, что 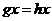 , но тогда , но тогда  . Следовательно существует биекция между множеством орбит и множеством левых смежных классов . Следовательно существует биекция между множеством орбит и множеством левых смежных классов 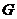 по по 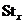 . Следовательно . Следовательно 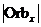 - это число различных смежных классов, а по теореме Лагранжа это равно - это число различных смежных классов, а по теореме Лагранжа это равно 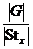 . . 
Следствие. 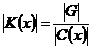 . .
Упражнение. Доказать, что если  , то , то 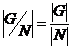 . .
Определение. Пусть 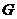 действует на действует на 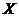 . Элемент . Элемент  называется неподвижным (инвариантным) относительно этого действия, если называется неподвижным (инвариантным) относительно этого действия, если 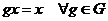 , т.е. если , т.е. если 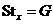 . .
Примеры:
1) При действии симметрической группы на многочлены неподвижными являются симметрические многочлены.
2) При действии 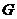 на себе сопряжением имеем, что элемент на себе сопряжением имеем, что элемент  неподвижен тогда и только тогда, когда неподвижен тогда и только тогда, когда 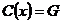 . Множество всех неподвижных элементов группы называется центром группы . Множество всех неподвижных элементов группы называется центром группы  (обозначается (обозначается  ). ).
Упражнение. 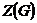 - нормальная абелевая подгруппа в - нормальная абелевая подгруппа в 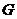 . .
Теорема. Пусть 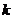 -поле, тогда -поле, тогда  . .
Доказательство.
Пусть  , если она неподвижна, то , если она неподвижна, то  . Распишем это равенство: . Распишем это равенство:
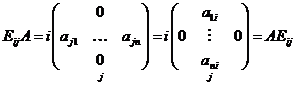 . .
В левой матрице на месте  стоит элемент стоит элемент 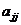 , а в правой , а в правой 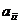 , следовательно , следовательно 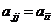 , а остальные элементы нули. Т.к. это верно для любых , а остальные элементы нули. Т.к. это верно для любых 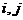 , то матрица , то матрица 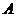 диагональная и по диагонали стоят одинаковые числа, т.е. диагональная и по диагонали стоят одинаковые числа, т.е. 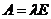 . . 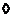
Упражнение. Найдите центры групп  и и 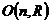 . .
Теорема. При 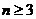  . .
Доказательство.
Возьмем 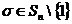 - любую не единичную подстановку. Разложим ее в произведение независимых циклов: - любую не единичную подстановку. Разложим ее в произведение независимых циклов: 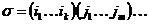
1) Пусть в этом разложении есть два цикла, т.е. 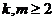 . Возьмем подстановку . Возьмем подстановку 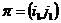 , тогда , тогда 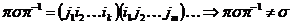 . .
2) Пусть в этом разложении есть хотя бы один цикл длины 3, т.е. 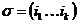 , , 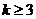 . Возьмем подстановку . Возьмем подстановку 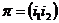 , тогда , тогда 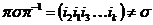 . .
3) Пусть в этом разложении есть только один цикл длины 2, т.е.  . Т.к. мы работаем в группе . Т.к. мы работаем в группе  при при  , то найдется , то найдется 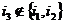 . Возьмем подстановку . Возьмем подстановку  , тогда , тогда  . .
Оставшийся случай - ни одного цикла - это и будет единичная подстановка. Следовательно неподвижной может быть только единичная подстановка. 
Упражнение. Докажите, что 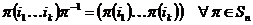 . .
Теорема. Две подстановки из 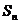 сопряжены тогда и только тогда, когда они имеют одинаковое цикловое строение, т.е. наборы длин циклов у них одинаковые. сопряжены тогда и только тогда, когда они имеют одинаковое цикловое строение, т.е. наборы длин циклов у них одинаковые.
Доказательство.
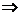 . Пусть . Пусть 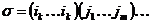 , тогда , тогда 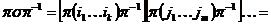  . Т.к. . Т.к. 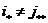 , то и , то и 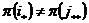 , следовательно, эти циклы независимые и мы получили такое же цикловое строение. , следовательно, эти циклы независимые и мы получили такое же цикловое строение.
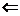 . Покажем на примере, как по данным двум подстановкам . Покажем на примере, как по данным двум подстановкам 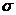 и и 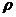 найти подстановку найти подстановку  , такую что , такую что 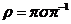 . Пусть . Пусть  и и 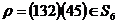 , тогда , тогда   , следовательно , следовательно 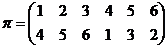 . . 
Определение. Группа 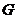 называется называется  -группой, если ее порядок является степенью простого числа -группой, если ее порядок является степенью простого числа  . .
Теорема. Если 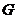 - - 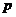 -группа, то -группа, то 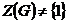 . .
Доказательство.
Разобьем 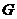 на классы сопряженных элементов (они не пересекаются) на классы сопряженных элементов (они не пересекаются)  . Одноэлементные классы состоят из одного центрального элемента. Если . Одноэлементные классы состоят из одного центрального элемента. Если 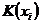 - не одноэлементный класс, то - не одноэлементный класс, то  - делится на - делится на 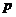 . Имеем, что . Имеем, что 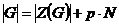 , где , где 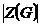 отвечает всем одноэлементным классам, а отвечает всем одноэлементным классам, а 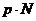 - не одноэлементным. Следовательно - не одноэлементным. Следовательно 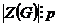 , следовательно , следовательно 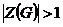 . . 
Следствие. Группа порядка  ( ( просто) абелева. просто) абелева.
Доказательство.
Если  , то по теореме , то по теореме 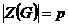 или или  . .
1) Пусть  , тогда , тогда 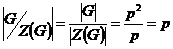 . Следовательно . Следовательно  циклическая, т.е. циклическая, т.е. 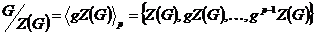 . Пусть . Пусть 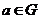 , тогда , тогда  и пусть и пусть 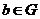 , тогда , тогда  , т.к. , т.к.  . Имеем, что . Имеем, что 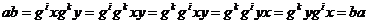 (элементы (элементы 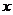 и и  перестановочны с перестановочны с  и друг с другом, т.к. они центральные). Следовательно и друг с другом, т.к. они центральные). Следовательно  - абелева и - абелева и  , т.е. , т.е. 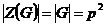 , получили противоречие с тем, что , получили противоречие с тем, что  . .
2) Если  , то , то  , следовательно, группа , следовательно, группа 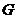 абелева. абелева. 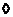
Лекция 4 (24.09.2001)
Теорема (1-ая теорема Силова). Пусть  - группа порядка - группа порядка  , где , где 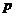 - простое число, тогда в группе - простое число, тогда в группе 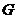 существует подгруппа порядка существует подгруппа порядка  . .
Доказательство.
Доказательство проведем по индукции по порядку группы.
База индукции.
Если  утверждение очевидно, в качестве подгруппы можно взять саму группу. утверждение очевидно, в качестве подгруппы можно взять саму группу.
Индуктивный переход.
1) Пусть в группе  существует нецентральный элемент, т.е. существует нецентральный элемент, т.е.  . Пусть . Пусть  - класс сопряженных элементов, содержащий - класс сопряженных элементов, содержащий 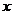 . Т.к. . Т.к.  , то , то  , кроме того , кроме того 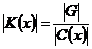 , где , где 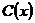 - это централизатор элемента - это централизатор элемента  . Мы знаем, что . Мы знаем, что  всегда является подгруппой. всегда является подгруппой.
1а) Пусть 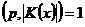 , тогда , тогда 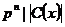 и и  . Тогда по предположению индукции (т.к. . Тогда по предположению индукции (т.к. 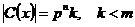 ) в ) в 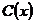 , а значит и в , а значит и в  , есть подгруппа порядка , есть подгруппа порядка 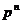 . .
1б) Пусть 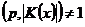 , т.е. , т.е. 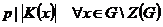 . Разобьем группу . Разобьем группу 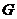 на непересекающиеся классы сопряженных элементов. на непересекающиеся классы сопряженных элементов.  , , 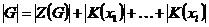 . Т.к. . Т.к.  , то , то 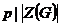 . .
Лемма. Пусть  - конечная абелева группа и - конечная абелева группа и 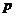 - простое число, делящее - простое число, делящее  , тогда в , тогда в  есть элемент порядка есть элемент порядка  . .
Доказательство.
Проведем индукция по порядку 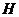 . .
База индукции: если 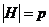 утверждение очевидно. утверждение очевидно.
Индуктивный переход.
1) Если порядок какого-нибудь элемента делится на  , то пусть , то пусть 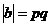 , тогда , тогда 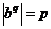 . .
2) Пусть порядок любого элемента не делится на 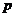 . Возьмем произвольный (не единичный) элемент . Возьмем произвольный (не единичный) элемент  . Рассмотрим . Рассмотрим 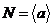 , тогда , тогда 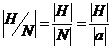 - делится на - делится на 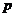 . По предположению индукции . По предположению индукции 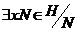 , т.ч. , т.ч. 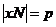 . Рассмотрим . Рассмотрим 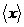 в в 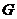 . Пусть . Пусть 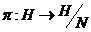 - естественный гомоморфизм - естественный гомоморфизм 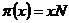 , тогда , тогда  . По теореме о гомоморфизме . По теореме о гомоморфизме 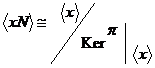 , тогда , тогда 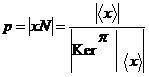 . Т.е. . Т.е. 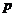 делит делит  . Т.е. порядок . Т.е. порядок 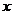 делится на делится на 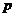 , что противоречит предположению пункта 2. Лемма доказана. , что противоречит предположению пункта 2. Лемма доказана. 
Вернемся к доказательству теоремы. Мы имеем, что 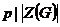 , причем , причем 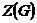 - абелева группа. По лемме в - абелева группа. По лемме в 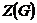 существует элемент существует элемент 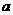 порядка порядка  . Пусть . Пусть 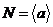 , тогда , тогда  и и 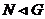 (т.к. (т.к.  - центральный элемент). Тогда - центральный элемент). Тогда 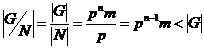 . По предположению индукции в . По предположению индукции в 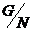 есть подгруппа есть подгруппа 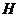 порядка порядка  . Рассмотрим естественный гомоморфизм . Рассмотрим естественный гомоморфизм  , рассмотрим полный прообраз подгруппы , рассмотрим полный прообраз подгруппы  : : 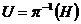 , т.е. , т.е. 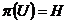 и и  . По теореме о гомоморфизме . По теореме о гомоморфизме 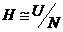 и и 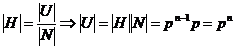 . .
2) Если в 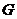 нет нецентральных элементов, то нет нецентральных элементов, то  , т.е. является абелевой группой. Рассуждая аналогично предыдущему пункту, применив лемму, получим утверждение теоремы. Теорема доказана. , т.е. является абелевой группой. Рассуждая аналогично предыдущему пункту, применив лемму, получим утверждение теоремы. Теорема доказана.  . .
Определение. Пусть  - конечная группа и - конечная группа и  , где , где 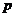 - простое число и - простое число и  . Тогда подгруппа в . Тогда подгруппа в 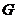 порядка порядка  называется силовской называется силовской 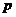 -подгруппой. -подгруппой.
Теорема (2-ая теорема Силова). Пусть  - конечная группа, - конечная группа, 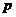 - простое число, делящее порядок группы. Тогда любая - простое число, делящее порядок группы. Тогда любая 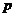 -подгруппа (подгруппа порядка -подгруппа (подгруппа порядка 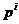 ) содержится в некоторой силовской, кроме того любые две силовские подгруппы сопряжены. ) содержится в некоторой силовской, кроме того любые две силовские подгруппы сопряжены.
Доказательство.
Пусть 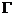 - - 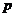 -подгруппа в -подгруппа в 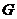 , , 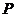 - силовская - силовская 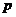 -подгруппа. Пусть -подгруппа. Пусть  . Определим действие: . Определим действие:  действует на действует на  на правилу: если на правилу: если 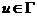 , то , то  . .  - не делится на - не делится на 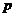 . Орбита . Орбита  . . 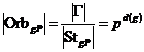 , где , где  - некая функция от - некая функция от 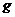 . Разобьем . Разобьем 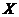 на непересекающиеся орбиты действия на непересекающиеся орбиты действия  . Если все орбиты не одноэлементные, то . Если все орбиты не одноэлементные, то 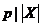 , что неверно. Следовательно, существует одноэлементная орбита, т.е. существует , что неверно. Следовательно, существует одноэлементная орбита, т.е. существует 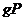 , такой что , такой что 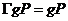 , что равносильно условию , что равносильно условию 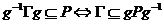 , но , но 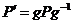 - силовская подгруппа. - силовская подгруппа.
Если  - силовская, то - силовская, то  , т.к. они имеют одинаковый порядок. Следовательно две силовские подгруппы сопряжены. , т.к. они имеют одинаковый порядок. Следовательно две силовские подгруппы сопряжены. 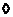
Теорема (3-я теорема Силова). Пусть 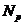 - число различных силовских - число различных силовских  -подгрупп в -подгрупп в 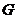 . Тогда . Тогда  делит делит 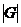 и и  . .
Доказательство.
Пусть  - множество всех силовских - множество всех силовских 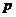 -подгрупп в -подгрупп в  , тогда , тогда 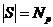 . На . На 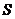 группа группа  действует сопряжением, т.е. если действует сопряжением, т.е. если 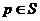 и и  , то , то 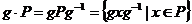 . По 2-ой теореме Силова множество . По 2-ой теореме Силова множество 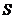 является орбитой любой силовской является орбитой любой силовской 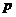 -подгруппы. Т.е. при таком действии существует всего одна орбита и -подгруппы. Т.е. при таком действии существует всего одна орбита и  , следовательно, , следовательно, 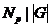 . .
Пусть 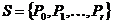 , рассмотрим действие , рассмотрим действие 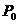 в в 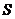 сопряжением. сопряжением. 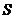 снова разбивается на орбиты, и порядок каждой из них делит снова разбивается на орбиты, и порядок каждой из них делит 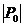 и потому является степенью числа и потому является степенью числа 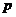 . Но . Но 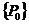 инвариантно относительно этого действия, т.е. инвариантно относительно этого действия, т.е. 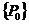 - это одноэлементная орбита. Пусть есть еще какая-нибудь одноэлементная орбита, например, - это одноэлементная орбита. Пусть есть еще какая-нибудь одноэлементная орбита, например, 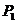 , т.е. , т.е.  . Пусть . Пусть 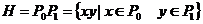 . .
Лемма. Множество 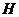 является подгруппой в является подгруппой в 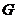 и и  . .
Доказательство.
Пусть  и и  . Тогда . Тогда
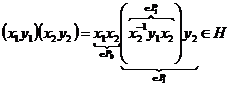 и и
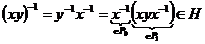 , т.е. , т.е.  - действительно является подгруппой. - действительно является подгруппой.
Пусть  и и  , где , где 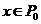 и и 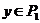 , тогда , тогда
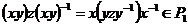 , т.е. , т.е. 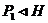 . Лемма доказана. . Лемма доказана. 
Завершим доказательство теоремы. Рассмотрим эту подгруппу 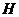 . Тогда . Тогда 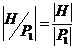 , т.е. , т.е. 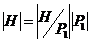 . Пусть . Пусть  - естественный гомоморфизм. Тогда - естественный гомоморфизм. Тогда 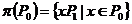 . Но если . Но если  , то , то 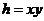 , где , где  и и 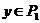 , тогда , тогда  , следовательно , следовательно  . В этом случае . В этом случае 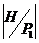 делит делит 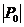 , т.е. , т.е. 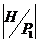 - степень числа - степень числа 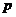 . Следовательно . Следовательно  - степень числа - степень числа  и и 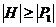 . Т.к. . Т.к. 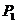 - силовская, что - силовская, что 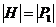 . Но . Но 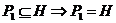 . Аналогично получаем, что и . Аналогично получаем, что и  . Но по предположению . Но по предположению 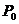 и и  различны, получили противоречие. различны, получили противоречие.
Итак в  только одна одноэлементная орбита ( только одна одноэлементная орбита ( ), значит порядок любой другой орбиты делится на ), значит порядок любой другой орбиты делится на 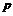 , следовательно, , следовательно,  . . 
Приложения теорем Силова.
1) Возьмем группу  , найдем силовские , найдем силовские 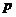 -подгруппы. мы знаем, что -подгруппы. мы знаем, что 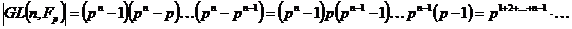 , т.е. , т.е. 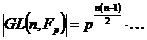 и силовская и силовская  -подгруппа имеет порядок -подгруппа имеет порядок  . Одна из силовских подгрупп - это подгруппа . Одна из силовских подгрупп - это подгруппа 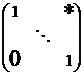 , остальные ей сопряжены, т.е. равны , остальные ей сопряжены, т.е. равны 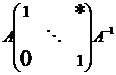 . .
2) Рассмотрим группу 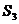 . .  . Ее силовские 2-подгруппы (всего их 3): . Ее силовские 2-подгруппы (всего их 3): 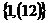 , , 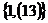 , ,  . Ее силовская 3-родгруппа (она всего одна): . Ее силовская 3-родгруппа (она всего одна): 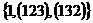 . .
3) Рассмотрим группу 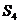 . . 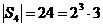 . Силовских 2-подгрупп всего может быть либо 1, либо 3. Возьмем . Силовских 2-подгрупп всего может быть либо 1, либо 3. Возьмем 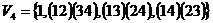 . Рассмотрим подгруппы . Рассмотрим подгруппы 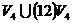 , , 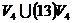 , ,  , … Они все силовские и среди них есть различные, следовательно всего существует три силовские 2-подгруппы. Силовские 3-подгруппы (всего их 4): , … Они все силовские и среди них есть различные, следовательно всего существует три силовские 2-подгруппы. Силовские 3-подгруппы (всего их 4):  , , 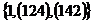 , ,  и и 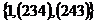 . .
Упражнение. Докажите, что если  - наименьшее простое число, делящее - наименьшее простое число, делящее 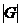 и и 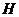 - подгруппа индекса - подгруппа индекса  (существует всего (существует всего 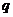 различных смежных классов различных смежных классов  по по 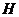 ), то ), то 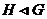 . .
|

 , тогда
, тогда 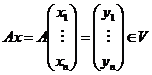 .
.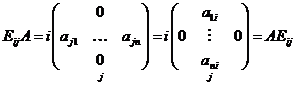 .
.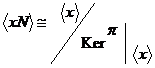 , тогда
, тогда 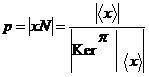 . Т.е.
. Т.е. 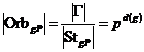 , где
, где 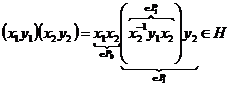 и
и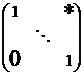 , остальные ей сопряжены, т.е. равны
, остальные ей сопряжены, т.е. равны 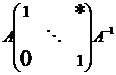 .
.