|
Определение. Пусть 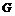 - группа. Положим - группа. Положим 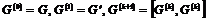 . Группа . Группа  называется разрешимой, если называется разрешимой, если 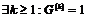 . .
Примеры:
1) абелевые группы разрешимы, т.е. 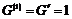 . .
2) 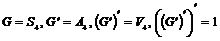 , т.к. , т.к. 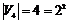 , следовательно, , следовательно, 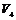 - абелевая группа. Следовательно, - абелевая группа. Следовательно, 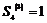 и и 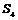 разрешима. разрешима.
3) При 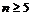 мы знаем, что мы знаем, что 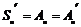 . Следовательно, . Следовательно, 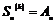 для любого для любого 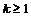 , и группа , и группа 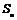 неразрешима. неразрешима.
Предложение. Пусть 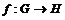 - гомоморфизм групп. Тогда - гомоморфизм групп. Тогда 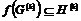 и, если и, если 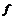 - сюръективно, то - сюръективно, то 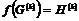 . .
Доказательство. (по индукции по 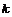 ) )
База индукции. 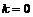 , оба утверждения верны. , оба утверждения верны.
1) Пусть для 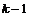 утверждение верно, докажем его для утверждение верно, докажем его для 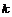 . . 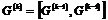 . Если . Если 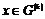 , то , то 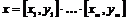 , где , где 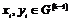 , тогда , тогда 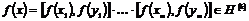 , т.к. по предположению индукции , т.к. по предположению индукции 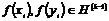 . .
2) Аналогично, пусть для 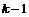 утверждение верно, докажем его для утверждение верно, докажем его для 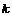 . Нам надо доказать, что для любого элемента . Нам надо доказать, что для любого элемента 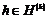 найдется найдется 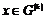 , такой что , такой что 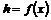 . Имеем, что . Имеем, что 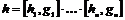 , где , где 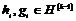 , по предположению индукции , по предположению индукции 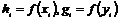 , где , где 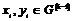 . Но тогда . Но тогда 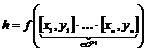 , следовательно, , следовательно, 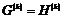 . . 
Предложение. 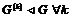 . .
Доказательство. (по индукции по 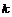 ) )
База индукции. 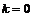 , утверждение верно. , утверждение верно.
Пусть утверждение верно для 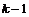 , докажем его для , докажем его для 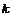 . Возьмем произвольный . Возьмем произвольный 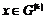 , тогда , тогда 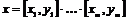 , где , где 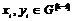 . Пусть . Пусть 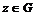 , тогда , тогда 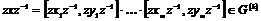 , т.к. по предположению индукции , т.к. по предположению индукции 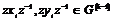 . Следовательно, . Следовательно, 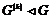 . . 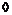
Упражнение. Пусть 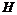 - подгруппа в - подгруппа в 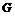 . Если . Если 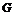 - разрешима, то - разрешима, то 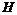 тоже разрешима. тоже разрешима.
Предложение. Если 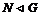 , то следующие два утверждения эквивалентны: , то следующие два утверждения эквивалентны:
1) 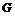 разрешима; разрешима;
2) 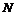 и и 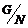 разрешимы. разрешимы.
Доказательство.
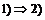 . .
В силу предыдущего упражнения 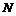 будет разрешима. Рассмотрим естественный гомоморфизм будет разрешима. Рассмотрим естественный гомоморфизм 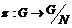 , , 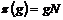 . Этот гомоморфизм всегда сюръективен, следовательно . Этот гомоморфизм всегда сюръективен, следовательно 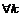 имеем, что имеем, что 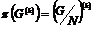 . Т.к. . Т.к. 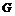 - разрешима, то - разрешима, то 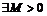 , такое что , такое что 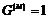 , следовательно , следовательно 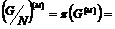 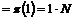 , следовательно , следовательно 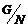 разрешима. разрешима.
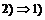 . .
Пусть 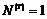 и и 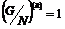 . Тогда . Тогда 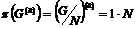 , следовательно, , следовательно, 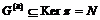 . Следовательно, . Следовательно, 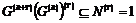 , т.е. , т.е. 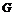 разрешима. разрешима. 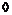
Теорема. Пусть 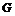 - группа. Следующие утверждения эквивалентны: - группа. Следующие утверждения эквивалентны:
1) 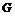 - разрешима; - разрешима;
2) существует ряд нормальных подгрупп 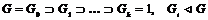 , такой, что , такой, что 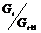 - абелева. - абелева.
Доказательство.
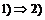 . .
Положим 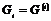 , тогда , тогда 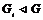 и и 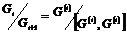 - абелева, т.к. фактор группа по коммутанту всегда абелева. - абелева, т.к. фактор группа по коммутанту всегда абелева.
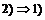 (по индукции по (по индукции по 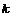 ). ).
База индукции, 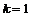 . Тогда . Тогда 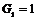 и и 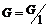 - абелева, следовательно, разрешима. - абелева, следовательно, разрешима.
Пусть утверждение верно для 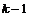 , докажем его для , докажем его для 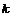 . В группе . В группе 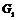 есть ряд длины есть ряд длины 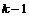 , следовательно, по предположению индукции , следовательно, по предположению индукции 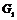 разрешима. Более того, разрешима. Более того, 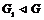 и и 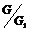 - абелева (разрешима), следовательно и - абелева (разрешима), следовательно и 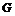 - разрешима. - разрешима. 
Теорема. Конечная 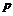 -группа разрешима. -группа разрешима.
Доказательство. (индукция по порядку группы).
База индукции, 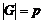 , следовательно , следовательно 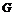 - абелева и разрешима. - абелева и разрешима.
Пусть утверждение верно для 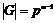 , докажем его для , докажем его для 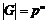 . Рассмотрим центр . Рассмотрим центр 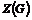 , мы знаем, что , мы знаем, что 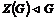 , , 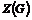 - абелева (разрешима) и - абелева (разрешима) и 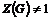 , т.е. , т.е. 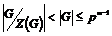 (разрешима по предположению индукции), следовательно и (разрешима по предположению индукции), следовательно и  разрешима. разрешима. 
Рассмотрим множество 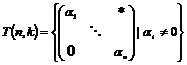 - множество верхнетреугольных матриц размера - множество верхнетреугольных матриц размера 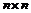 с ненулевыми числами поля с ненулевыми числами поля 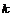 на диагонали. Рассмотрим еще множество на диагонали. Рассмотрим еще множество 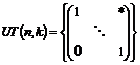 - подмножество в - подмножество в 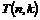 с единицами на диагонали. с единицами на диагонали.
Упражнение. Докажите, что 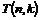 - группа по умножению матриц, а - группа по умножению матриц, а 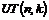 подгруппа в ней. подгруппа в ней.
Предложение. 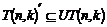 и и 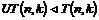 . .
Доказательство.
Рассмотрим отображение 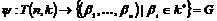 , отображение в , отображение в 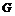 - множество наборов из - множество наборов из  ненулевых чисел поля ненулевых чисел поля 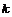 . Это отображение действует по правилу . Это отображение действует по правилу 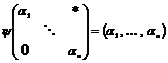 . Введем операцию умножения в множестве . Введем операцию умножения в множестве 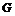 : : 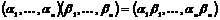 . Теперь . Теперь 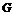 - это абелевая группа и - это абелевая группа и 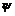 - гомоморфизм групп, причем - гомоморфизм групп, причем  , следовательно , следовательно 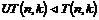 . Следовательно . Следовательно 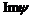 - это абелевая группа, изоморфная - это абелевая группа, изоморфная 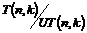 , т.е. , т.е. 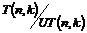 - абелева. Рассмотрим естественный гомоморфизм - абелева. Рассмотрим естественный гомоморфизм 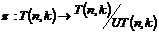 , тогда , тогда 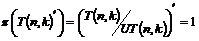 . Следовательно, . Следовательно, 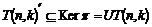 . . 
Теорема. Группа 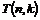 всегда разрешима. всегда разрешима.
Доказательство.
Для доказательства теоремы, нам достаточно доказать разрешимость группы 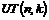 и воспользоваться предыдущим предложением. Докажем это по индукции по и воспользоваться предыдущим предложением. Докажем это по индукции по  . .
База индукции, 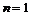 . . 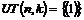 - разрешима. - разрешима.
Пусть утверждение верно для 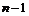 , докажем его для , докажем его для 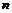 . Рассмотрим отображение . Рассмотрим отображение 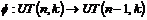 , определенное по следующему правилу: пусть , определенное по следующему правилу: пусть 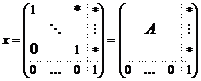 , тогда , тогда 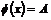 . Если . Если 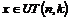 , то , то 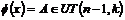 . .
Лемма. 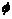 - гомоморфизм групп. - гомоморфизм групп.
Доказательство.
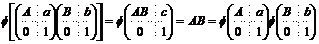 . . 
Рассмотрим 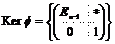 , т.к. , т.к. 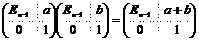 , то , то 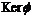 - абелева группа (разрешима). Кроме того - абелева группа (разрешима). Кроме того 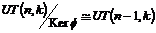 - по предположению индукции разрешима. Следовательно - по предположению индукции разрешима. Следовательно 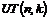 разрешима и разрешима и 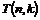 разрешима. разрешима. 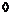
|

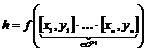 , следовательно,
, следовательно, 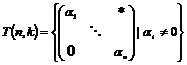 - множество верхнетреугольных матриц размера
- множество верхнетреугольных матриц размера 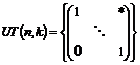 - подмножество в
- подмножество в 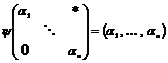 . Введем операцию умножения в множестве
. Введем операцию умножения в множестве 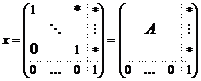 , тогда
, тогда