|
Определение. Пусть 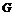 - группа и - группа и 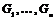 ее нормальные подгруппы. Тогда ее нормальные подгруппы. Тогда  является прямым (внутренним) произведением групп является прямым (внутренним) произведением групп 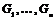 , если каждый элемент группы , если каждый элемент группы 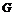 имеет и притом единственное представление имеет и притом единственное представление  , где , где  . Обозначается . Обозначается 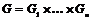 (если операция в группе - сложение, то обозначается (если операция в группе - сложение, то обозначается 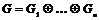 - прямая сумма). - прямая сумма).
Упражнение. Докажите, что 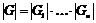 . .
Предложение. Если  и и 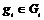 , ,  , , 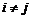 , то , то 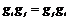 . .
Доказательство.
Рассмотрим коммутатор 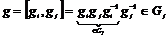 , аналогично , аналогично 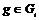 . Следовательно, . Следовательно, 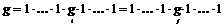 , в силу единственности разложения имеем, что , в силу единственности разложения имеем, что 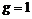 , т.е. , т.е.  . . 
Следствие. Пусть  , ,  , тогда , тогда  и и  . .
Доказательство.
 , здесь элемент , здесь элемент  перестановочен с элементами перестановочен с элементами 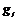 и и 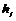 при при 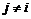 по предложению. по предложению.
Имеем  . . 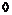
Пример.
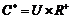 , где , где  - окружность единичного радиуса, - окружность единичного радиуса, 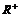 - положительные вещественные числа. Т.е. любое число - положительные вещественные числа. Т.е. любое число 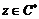 представимо и притом однозначно в виде представимо и притом однозначно в виде  . .
Лекция 7 (15.10.2001)
Теорема. Группа 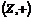 не представима в виде прямой суммы. не представима в виде прямой суммы.
Доказательство. (от противного)
Допустим, что 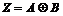 , где , где 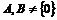 , тогда , тогда 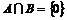 . Возьмем . Возьмем  и и  , ,  . Рассмотрим элемент . Рассмотрим элемент  , он , он  и и 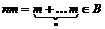 . Получили, что . Получили, что 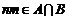 и и 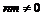 - противоречие с - противоречие с 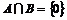 . . 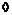
Теорема. Пусть 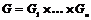 и и  , , 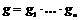 , где , где  . Тогда . Тогда 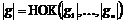 . .
Доказательство.
Имеем 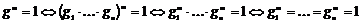 . Следовательно, . Следовательно, 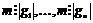 , т.е. , т.е.  - это общее кратное порядков элементов - это общее кратное порядков элементов  . Значит минимальное такое . Значит минимальное такое 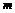 - НОК порядков. - НОК порядков. 
Посмотрим, как раскладываются в прямые суммы конечные циклические группы (только что мы доказали, что бесконечные циклические группы не раскладывается, т.к. они изоморфны  ). ).
Теорема. Если  - конечная группа и - конечная группа и  , то следующие условия эквивалентны: , то следующие условия эквивалентны:
1)  - циклическая; - циклическая;
2)  - циклические и их порядки - циклические и их порядки  взаимно просты. взаимно просты.
Доказательство.
 . .  - являются подгруппами в - являются подгруппами в  , следовательно, они циклические. Возьмем произвольный , следовательно, они циклические. Возьмем произвольный  , , 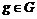 , , 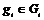 . Пусть порядки . Пусть порядки  не взаимно просты, тогда не взаимно просты, тогда 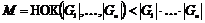 . Тогда . Тогда 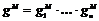 , по следствию из теоремы Лагранжа , по следствию из теоремы Лагранжа 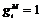 , т.к. , т.к.  . Следовательно, порядок каждого элемента . Следовательно, порядок каждого элемента  , т.е. группа , т.е. группа 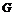 не циклическая. Получили противоречие с тем, что порядки не циклическая. Получили противоречие с тем, что порядки 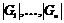 не взаимно просты. не взаимно просты.
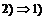 . Имеем, что . Имеем, что 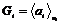 и и  при при 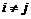 . Возьмем элемент . Возьмем элемент  , тогда , тогда  , следовательно , следовательно  . . 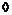
Следствие 1. Пусть  - простое число. Циклическая группа порядка - простое число. Циклическая группа порядка  не разложима. не разложима.
Следствие 2. Если 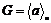 и и 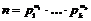 , тогда , тогда  . .
Доказательство.
Группа  состоит из элементов группы состоит из элементов группы  и ее порядок равен порядок равен и ее порядок равен порядок равен  . . 
|










