|
Кольцом называется абелевая группа по сложению с операцией умножения 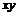 , для которой выполнены следующие свойства: , для которой выполнены следующие свойства: 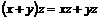 и и 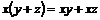 . .
Кольцо называется коммутативным, если 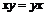 . .
Кольцо называется ассоциативным, если 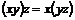 . .
Кольцо называется антикоммутативным, если 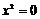 . .
Кольцо называется кольцом Ли, если 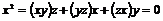 . .
В любом кольце 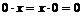 . Действительно . Действительно 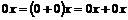 и и 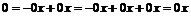 . .
Элемент 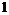 в кольце называется единицей, если в кольце называется единицей, если 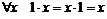 . .
Определение. Полем называется коммутативное, ассоциативное кольцо с единицей, в котором у каждого ненулевого элемента есть обратный.
Определение. Телом называется ассоциативное кольцо с единицей, в котором каждый ненулевой элемент обратим.
Примеры:
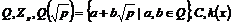
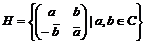 - поле кватернионов. Это действительно будет полем, т.к. - поле кватернионов. Это действительно будет полем, т.к.  , если матрица ненулевая, следовательно у нее существует обратная: , если матрица ненулевая, следовательно у нее существует обратная: 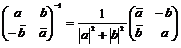 . .
Определение. Пусть 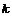 - поле. Кольцо - поле. Кольцо 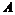 , являющееся векторным пространством над , являющееся векторным пространством над 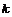 , называется , называется 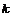 - алгеброй, если - алгеброй, если 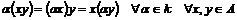 . .
Упражнение. В антикоммутативной алгебре (кольце) выполнено тождество 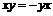 . .
Упражнение. Пусть 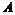 - ассоциативная алгебра, положим - ассоциативная алгебра, положим 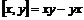 . Докажите, что . Докажите, что 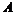 относительно нового умножения относительно нового умножения 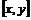 является алгеброй Ли. является алгеброй Ли.
Определение. Элемент 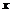 алгебры алгебры 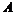 с единицей называется обратимым, если с единицей называется обратимым, если 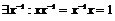 . .
Определение. Элемент 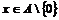 называется левым (правым) делителем нуля, если называется левым (правым) делителем нуля, если 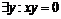 ( (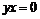 ). ).
Предложение. Все обратимые элементы ассоциативной алгебры с единицей образуют группу по умножению. Обратимый элемент не может быть делителем нуля.
Доказательство.
Если 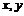 - обратимы, тогда - обратимы, тогда 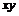 - обратим, - обратим, 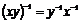 . .
Если 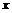 - обратим, то и - обратим, то и 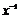 - обратим, - обратим, 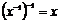 . .
Следовательно это действительно группа по умножению.
Пусть 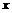 обратим и обратим и 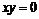 , тогда , тогда 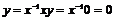 , что противоречит определению делителя нуля. , что противоречит определению делителя нуля. 
Определение. Алгебра называется областью, если в ней нет делителей нуля.
Определение. Подалгеброй 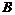 в алгебре в алгебре 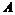 называется подпространство, являющееся кольцом, для которого выполнены свойства: называется подпространство, являющееся кольцом, для которого выполнены свойства:
1) 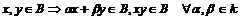 , ,
2) 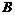 не пусто. не пусто.
Пусть 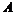 - ассоциативная - ассоциативная 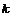 -алгебра с единицей, и пусть -алгебра с единицей, и пусть 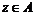 . Рассмотрим множество . Рассмотрим множество 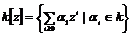 - все такие конечные суммы. - все такие конечные суммы.
Упражнение. 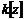 является наименьшей подалгеброй с единицей в является наименьшей подалгеброй с единицей в 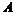 , содержащей элемент , содержащей элемент 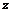 . .
Определение. Идеалом 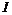 кольца (алгебры) называется подгруппа аддитивной группы (подпространство), такая что если кольца (алгебры) называется подгруппа аддитивной группы (подпространство), такая что если 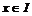 , , 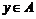 , то , то 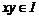 и и 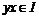 . Т.е. идеал выдерживает умножение слева и справа на все элементы кольца (алгебры). . Т.е. идеал выдерживает умножение слева и справа на все элементы кольца (алгебры).
Определение. Кольцо (алгебра) называется простым, если в нем всего два идеала: 0 и оно само.
Предложение. Пусть в ассоциативной алгебре с единицей идеал содержит обратимый элемент, тогда идеал совпадает со всей алгеброй.
Доказательство.
Пусть 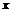 - обратимый и - обратимый и 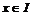 . Если . Если 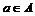 , то , то 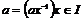 , следовательно , следовательно 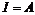 . . 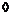
Следствие. Любое тело, любое поле всегда просты.
Пусть  - ассоциативная коммутативная алгебра с 1 и - ассоциативная коммутативная алгебра с 1 и 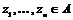 . Рассмотрим множество . Рассмотрим множество 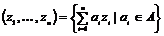 . .
Упражнение. 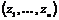 - идеал в - идеал в 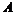 , содержащий , содержащий 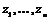 . .
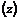 называется главным идеалом, порожденным элементом называется главным идеалом, порожденным элементом 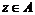 . .
Лекция 12 (19.11.2001)
Определение. Коммутативная ассоциативная область (без делителей нуля) с единицей называется кольцом (алгеброй) главных идеалов, если в нем любой идеал главный.
Например в кольце целых чисел 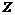 любой идеал всегда подгруппа, т.е. любой идеал всегда подгруппа, т.е. 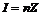 , т.е. любой идеал главный и это кольцо главных идеалов. , т.е. любой идеал главный и это кольцо главных идеалов.
Теорема. Пусть 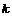 - поле. Тогда - поле. Тогда 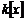 - кольцо главных идеалов. - кольцо главных идеалов.
Доказательство.
Пусть 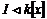 и и 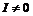 . Пусть . Пусть 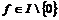 - многочлен наименьшей степени. Пусть - многочлен наименьшей степени. Пусть 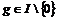 , тогда мы можем поделить , тогда мы можем поделить 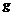 на на 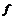 с остатком: с остатком: 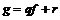 , где либо , где либо 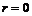 , либо , либо 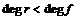 . Но . Но 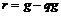 , следовательно, , следовательно, 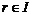 . Т.к. у . Т.к. у 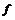 была наименьшая степень, то была наименьшая степень, то 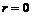 , т.е. , т.е. 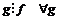 . Следовательно . Следовательно 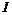 - главный идеал, порожденный многочленом - главный идеал, порожденный многочленом 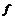 и и 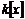 - кольцо главных идеалов. - кольцо главных идеалов. 
Упражнение. Доказать, что кольцо 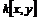 не является кольцом главных идеалов. Указание: рассмотреть идеал не является кольцом главных идеалов. Указание: рассмотреть идеал 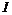 - все многочлены с нулевым свободных членов и доказать, что он не является главным. - все многочлены с нулевым свободных членов и доказать, что он не является главным.
Рассмотрим кольцо 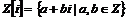 . .
Теорема. 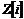 - кольцо главных идеалов. - кольцо главных идеалов.
Доказательство.
Выведем на этом множестве аналог алгоритма Евклида (деление с остатком). Введем норму 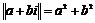 , тогда , тогда 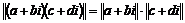 . .
Лемма. Пусть 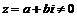 , тогда , тогда 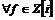 существуют такие существуют такие 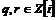 , что , что 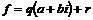 , причем , причем 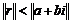 . .
Доказательство.
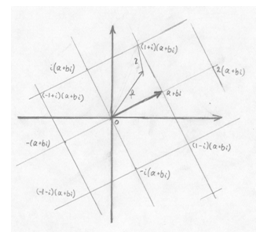 Рассмотрим все числа вида Рассмотрим все числа вида 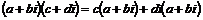 . Получим что-то типа решетки, сторона квадрата - это . Получим что-то типа решетки, сторона квадрата - это 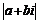 . Возьмем произвольное число . Возьмем произвольное число 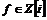 . Оно попадет в один из таких квадратов, тогда расстояние от не до какой-то вершины квадрата будет не больше . Оно попадет в один из таких квадратов, тогда расстояние от не до какой-то вершины квадрата будет не больше 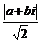 . .
В качестве числа 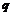 возьмем такое число, чтобы возьмем такое число, чтобы 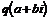 была эта вершина. была эта вершина. 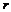 - вектор от этой вершины до - вектор от этой вершины до 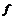 . Тогда . Тогда 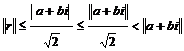 . . 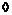
Пусть теперь 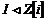 , ,  . Выберем . Выберем 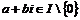 такое, что его норма минимальна. Далее рассуждая также как и в прошлой теореме с многочленами (применяя описанное выше деление с остатком), получаем, что все остальные числа делятся на него, т.е. такое, что его норма минимальна. Далее рассуждая также как и в прошлой теореме с многочленами (применяя описанное выше деление с остатком), получаем, что все остальные числа делятся на него, т.е. 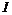 - главный идеал и - главный идеал и 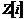 - кольцо главных идеалов. - кольцо главных идеалов. 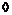
Теперь мы перейдем к рассмотрению некоммутативных колец. Пусть 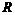 - ассоциативное кольцо с единицей, - ассоциативное кольцо с единицей, 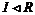 . Пусть . Пусть 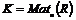 - квадратные матрицы с коэффициентами из кольца - квадратные матрицы с коэффициентами из кольца 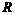 . .
Упражнение. 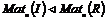 . .
Теорема. Пусть 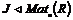 . Тогда . Тогда 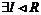 , такой что , такой что 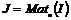 . .
Доказательство.
Пусть 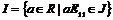 . Докажем, что . Докажем, что 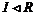 . Пусть . Пусть 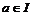 и и 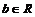 , тогда , тогда 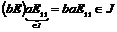 , следовательно, , следовательно, 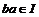 . Аналогично . Аналогично 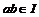 , следовательно, , следовательно, 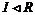 . .
Пусть 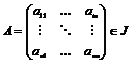 , тогда , тогда 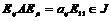 . Следовательно, . Следовательно, 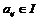 , т.е. все коэффициенты матриц из , т.е. все коэффициенты матриц из 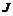 содержатся в идеале содержатся в идеале 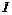 . Следовательно . Следовательно 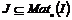 . Пусть . Пусть 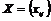 , , 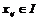 - произвольная матрица из - произвольная матрица из 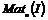 . Тогда . Тогда 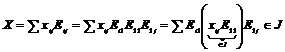 . Следовательно . Следовательно 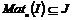 , т.е. , т.е. 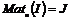 . . 
Напомним, что кольцо (алгебра) 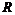 называется простым, если в нем только два идеала: ноль и оно само. называется простым, если в нем только два идеала: ноль и оно само.
Следствие. Если 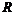 - тело, то - тело, то 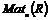 - простое кольцо. - простое кольцо.
Определение. Отображение 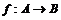 называется гомоморфизмом алгебр, если называется гомоморфизмом алгебр, если
1) 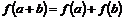 , ,
2) 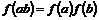 , ,
3) 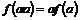 . .
Изоморфизмом называется биективный гомоморфизм.
Автоморфизмом называется изоморфизм алгебры на себя.
Мономорфизмом называется инъективный гомоморфизм.
Эпиморфизмом называется сюръективный гомоморфизм.
Ядром гомоморфизма называется полный прообраз нуля 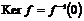 . .
Предложение. 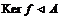 . .
Доказательство.
Пусть 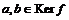 , тогда , тогда 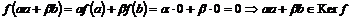 . .
Пусть 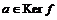 , , 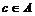 , тогда , тогда 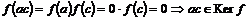 . . 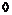
Упражнение. 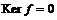 тогда и только тогда, когда тогда и только тогда, когда 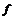 - мономорфизм. - мономорфизм.
Пусть 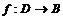 , где , где 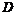 - тело. Тогда - тело. Тогда 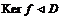 , но в , но в 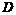 всего для идеала: ноль и оно само. Следовательно, либо всего для идеала: ноль и оно само. Следовательно, либо 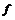 - нулевой, либо мономорфизм. - нулевой, либо мономорфизм.
Пусть 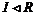 , тогда , тогда 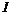 - подгруппа в - подгруппа в 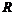 (по сложению), причем нормальная, следовательно (по сложению), причем нормальная, следовательно 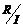 - факторгруппа (по сложению), т.е. - факторгруппа (по сложению), т.е. 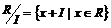 . Тогда . Тогда
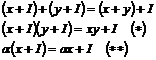
Предложение. Умножение  и умножение на скаляры и умножение на скаляры 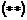 определены корректно. определены корректно.
Доказательство.
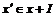 , , 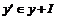 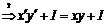 . .
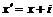 , , 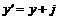 , , 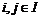 . .
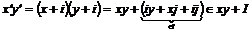 . .
Следовательно умножение 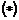 определено корректно. определено корректно.
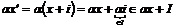 . .
Следовательно умножение на скаляры 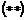 определено корректно. определено корректно. 
Идеалы и факторгруппы строятся в любом кольце (не только в ассоциативном или коммутативном). 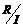 - факторалгебра (факторкольцо). - факторалгебра (факторкольцо).
Рассмотрим гомоморфизм 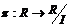 , т.ч. , т.ч. 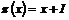 (естественный гомоморфизм). (естественный гомоморфизм).
Упражнение. 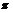 является эпиморфизмом и является эпиморфизмом и 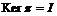 . .
Теорема (о гомоморфизме). Пусть 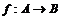 , тогда , тогда 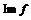 - подалгебра, изоморфная - подалгебра, изоморфная 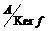 . .
Доказательство.
Определим изоморфизм 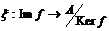 следующим образом: следующим образом: 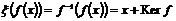 (см. теорему о гомоморфизме в теории групп). Проверим некоторые свойства изоморфизма (остальные проверены в теории групп): (см. теорему о гомоморфизме в теории групп). Проверим некоторые свойства изоморфизма (остальные проверены в теории групп):
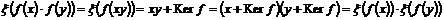
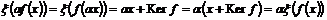 , следовательно это изоморфизм. , следовательно это изоморфизм. 
Примеры:
1) 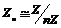 . Гомоморфизм . Гомоморфизм 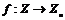 , где , где 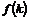 - остаток от деления - остаток от деления 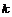 на на 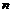 , тогда , тогда 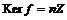 . .
2) 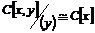 . Гомоморфизм . Гомоморфизм 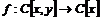 , где , где 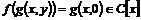 , тогда , тогда 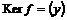 . .
3) 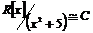 . Гомоморфизм . Гомоморфизм 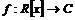 , где , где 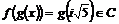 , тогда , тогда 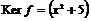 . .
Если 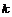 - подполе в - подполе в 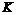 , тогда , тогда 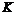 является алгеброй над является алгеброй над 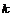 . Все автоморфизмы . Все автоморфизмы 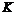 как алгебры над как алгебры над  образуют группу Галуа образуют группу Галуа 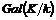 . .
| 
 Рассмотрим все числа вида
Рассмотрим все числа вида 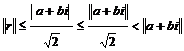 .
. 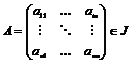 , тогда
, тогда 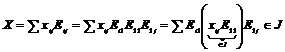 . Следовательно
. Следовательно