|
Определение. Абелевая группа 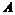 называется конечно-порожденной, если называется конечно-порожденной, если 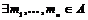 , такие что , такие что 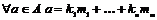 , где , где 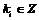 . .
Упражнение. Доказать, что 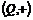 не конечно-порожденная. не конечно-порожденная.
Определение. Абелевая группа 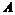 называется свободной, если в ней есть базис, т.е. такой набор элементов называется свободной, если в ней есть базис, т.е. такой набор элементов 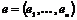 , что , что 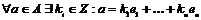 . .
Теорема. Абелевая группа 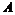 свободна тогда и только тогда, когда свободна тогда и только тогда, когда 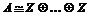 . .
Доказательство.
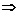 . Пусть . Пусть 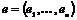 - базис - базис 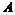 , тогда если , тогда если 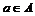 , то , то 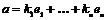 , , 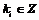 . Возьмем отображение . Возьмем отображение 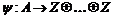 по правилу по правилу 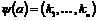 . . 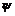 - это изоморфизм, следовательно - это изоморфизм, следовательно 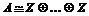 . .
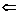 . Пусть . Пусть 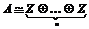 . Предъявим базис в . Предъявим базис в 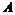 : : 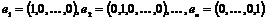 , тогда , тогда 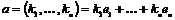 . . 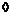
Определение. Ранг свободной абелевой группы равен числу векторов в базисе.
Теорема. Ранг свободной абелевой группы определен однозначно.
Доказательство.
Мы докажем эту теорему немного необычным, но красивым способом.
Пусть 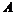 имеем базис имеем базис 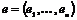 , рассмотрим группу , рассмотрим группу 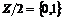 . Пусть . Пусть 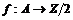 - гомоморфизм. Если - гомоморфизм. Если 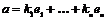 , то , то 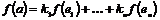 . Таким образом . Таким образом 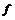 однозначно задается значениями на базисных элементах: однозначно задается значениями на базисных элементах: 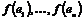 . Следовательно всего различных гомоморфизмов будет . Следовательно всего различных гомоморфизмов будет 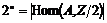 . Пусть в . Пусть в 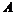 есть базис из есть базис из 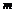 элементов, тогда элементов, тогда 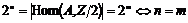 . . 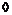
Теорема. Пусть  - свободная абелевая группа ранга - свободная абелевая группа ранга 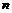 и и 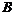 - подгруппа в - подгруппа в 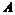 . Тогда . Тогда 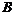 - свободная абелевая группа ранга - свободная абелевая группа ранга 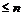 . .
Примечание. В подобной теореме о размерности линейных пространств из совпадения размерностей. следовало совпадение подгруппы с самой группой, однако здесь это не верно. Пример: группа 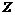 и подгруппа и подгруппа 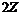 имеют ранг имеют ранг 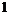 . .
Доказательство. (по индукции)
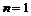 , имеем, что , имеем, что 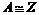 и утверждение теоремы выполнены, т.к. любая бесконечная подгруппа и утверждение теоремы выполнены, т.к. любая бесконечная подгруппа 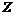 является изоморфной является изоморфной 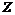 , т.е. свободной абелевой ранга , т.е. свободной абелевой ранга 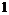 . .
Пусть для 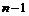 теорема доказана. Докажем ее для теорема доказана. Докажем ее для 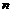 . Пусть . Пусть 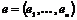 - базис в - базис в 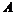 . Рассмотрим множество . Рассмотрим множество 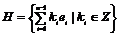 - линейная оболочка первых - линейная оболочка первых 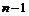 базисных элементов (является свободной абелевой группой с базисом базисных элементов (является свободной абелевой группой с базисом  . Рассмотрим отображение . Рассмотрим отображение 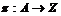 такое, что если такое, что если 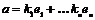 , то , то 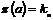 . Тогда . Тогда 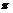 - это эпиморфизм и - это эпиморфизм и  . . 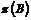 - это подгруппа в - это подгруппа в 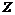 . .
Если 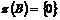 , то , то 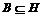 и (по предположению индукции) и (по предположению индукции) 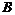 - свободная абелевая группа ранга - свободная абелевая группа ранга 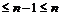 . .
Если 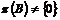 , то , то 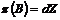 . . 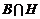 - свободная подгруппа в - свободная подгруппа в 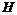 с базисом с базисом 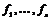 , , 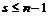 (по предположению индукции), следовательно (по предположению индукции), следовательно 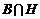 - свободная подгруппа в - свободная подгруппа в 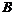 . . 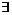 элемент элемент 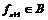 , такой что , такой что 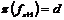 . Покажем, что . Покажем, что 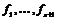 - базис в - базис в 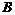 , , 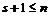 . .
Пусть 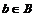 , тогда , тогда 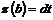 , , 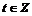 , тогда , тогда 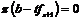 , следовательно, , следовательно, 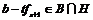 . Т.е. . Т.е. 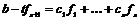 и и 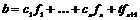 . Существование представления мы доказали, осталось доказать его единственность, для этого достаточно доказать, что из . Существование представления мы доказали, осталось доказать его единственность, для этого достаточно доказать, что из 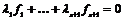 следует, что все следует, что все  . Имеем . Имеем 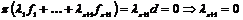 и от нашего равенства остается и от нашего равенства остается 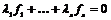 . Следовательно, т.к. . Следовательно, т.к. 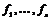 - базис в - базис в 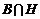 и все остальные коэффициенты и все остальные коэффициенты 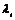 равны нулю. равны нулю. 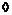
|










