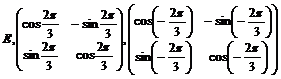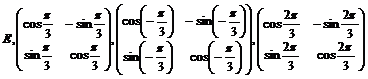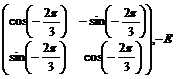|
Пусть нам задано евклидово пространство 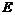 размерности размерности 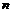 . Пусть нам также задана метрика . Пусть нам также задана метрика 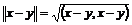 , где , где 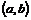 - скалярное произведение векторов - скалярное произведение векторов 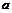 и и 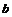 . Движение пространства . Движение пространства  - это биективное преобразование - это биективное преобразование 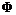 пространства пространства 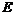 , сохраняющее расстояние между векторами, т.е. , сохраняющее расстояние между векторами, т.е. 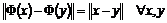 . .
Упражнение. Будет ли произвольное преобразование, сохраняющее длины, биекцией?
Теорема. Пусть 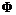 - движение, тогда - движение, тогда 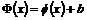 , где , где 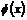 - ортогональное преобразование - ортогональное преобразование 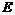 и и  - некоторый вектор. Также верно и обратное утверждение. - некоторый вектор. Также верно и обратное утверждение.
Доказательство этой теоремы было в курсе Линейной Алгебры. 
Рассмотрим множество 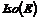 - все движения пространства - все движения пространства 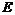 . .
Теорема. 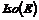 - группа относительно операции композиции преобразований. - группа относительно операции композиции преобразований.
Доказательство.
Пусть  и и  , тогда , тогда 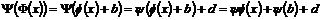 - снова движение. - снова движение.
Единичное преобразование - это тождественное преобразование.
Обратное преобразование - это  . . 
Рассмотрим множество 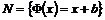 - множество всех сдвигов. Из формулы последней теоремы видно, что - множество всех сдвигов. Из формулы последней теоремы видно, что  - это подгруппа в - это подгруппа в 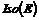 . Рассмотрим также множество . Рассмотрим также множество 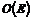 - множество всех ортогональных преобразований - множество всех ортогональных преобразований 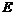 , это множество также будет подгруппой в , это множество также будет подгруппой в 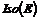 . .
По первой теореме произвольное преобразование имеет вид  . В этой записи вектор . В этой записи вектор  определен однозначно, т.к. определен однозначно, т.к. 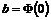 . Следовательно и ортогональное преобразование . Следовательно и ортогональное преобразование 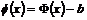 определено однозначно. Это преобразование определено однозначно. Это преобразование  называется дифференциалом преобразования называется дифференциалом преобразования  и обозначается и обозначается 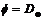 . .
Из формулы второй теоремы имеем, что 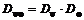 , т.е. дифференциал обладает свойством мультипликативности. , т.е. дифференциал обладает свойством мультипликативности.
Теорема. Сопоставление движению  его дифференциала его дифференциала  является эпиморфизмом является эпиморфизмом 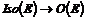 , причем ядро этого эпиморфизма равно , причем ядро этого эпиморфизма равно 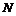 . .
Доказательство.
То, что это гомоморфизм групп следует из свойства мультипликативности дифференциала. Если 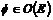 , то , то  , следовательно этот гомоморфизм сюръективен (т.е. это эпиморфизм). Ядро - это все движения, дифференциал которых равен тождественному преобразованию, т.е. все движения вида , следовательно этот гомоморфизм сюръективен (т.е. это эпиморфизм). Ядро - это все движения, дифференциал которых равен тождественному преобразованию, т.е. все движения вида 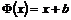 , т.е. множество сдвигов , т.е. множество сдвигов 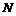 . . 
Следствие. 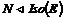 и и 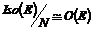 . .
Предложение.  . .
Доказательство.
Пусть  - сдвиг на вектор - сдвиг на вектор 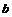 , сопоставим такому преобразованию этот вектор , сопоставим такому преобразованию этот вектор 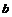 . Тогда, если . Тогда, если 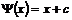 - сдвиг на вектор - сдвиг на вектор 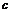 , ,  - сдвиг на вектор - сдвиг на вектор  . Это сопоставление преобразованию вектора является биективным, следовательно . Это сопоставление преобразованию вектора является биективным, следовательно 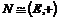 . . 
Определение. Подгруппа 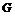 в в  называется кристалло-графической, если называется кристалло-графической, если
1) 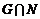 - дискретная подгруппа группы - дискретная подгруппа группы 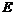 ранга ранга  , ,
2) 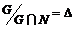 - конечная группа. - конечная группа.
Опишем все кристалло-графические группы в двумерном случае.
Предложение. Если 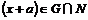 и и 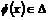 , то , то  . .
Доказательство.
Пусть  - сдвиг на - сдвиг на 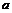 , и , и 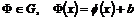 - преобразование с дифференциалом - преобразование с дифференциалом 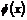 . Тогда . Тогда 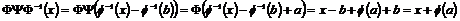 , следовательно , следовательно 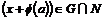 (т.к. (т.к.  - нормальна). - нормальна). 
Пусть 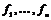 - базис в - базис в 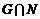 (это также будет базис во всем линейном пространстве (это также будет базис во всем линейном пространстве  ). В группе ). В группе  лежат все целочисленные комбинации этих векторов, т.е. целочисленная решетка, порожденная этими векторами. Предыдущим упражнением мы доказали, что группа лежат все целочисленные комбинации этих векторов, т.е. целочисленная решетка, порожденная этими векторами. Предыдущим упражнением мы доказали, что группа 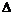 переводит эту решетку в себя. Матрица любого оператора переводит эту решетку в себя. Матрица любого оператора 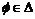 целочисленная в базисе целочисленная в базисе 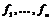 , т.е. , т.е.  - это целое число. - это целое число.
Группа  называется пространственной группой. называется пространственной группой.
Группа  называется точечной группой. называется точечной группой.
Теорема. Пусть 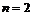 и и  - группа ортогональных операторов с определителем - группа ортогональных операторов с определителем  (т.е. (т.е.  содержит только собственные преобразования). Тогда содержит только собственные преобразования). Тогда 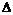 - циклическая группа порядка - циклическая группа порядка 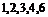 . .
Доказательство.
Пусть 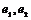 - ортогональный базис пространства - ортогональный базис пространства 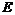 и и  , тогда его матрица имеет вид , тогда его матрица имеет вид 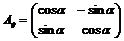 . Кроме того, ее след . Кроме того, ее след 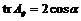 - целое число. Следовательно - целое число. Следовательно 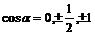 , т.е. , т.е. 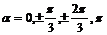 . Укажем все возможные варианты группы . Укажем все возможные варианты группы  в зависимости о того, какие повороты в ней лежат: в зависимости о того, какие повороты в ней лежат:
повороты, лежащие в группе |
элементы группы |
порядок |

|
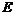
|
1 |
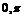
|
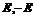
|
2 |

|
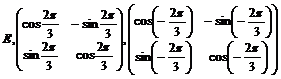
|
3 |

|
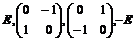
|
4 |

|
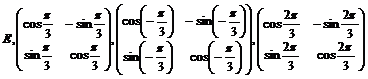
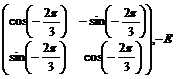
|
6 |
В этой таблице не все матрицы целочисленные, однако существуют такие базисы (для каждого случая он свой), что в них эти матрицы будут целочисленными. Например, в базисе 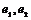 , где вектор , где вектор 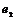 повернут относительно повернут относительно  на угол на угол  матрица поворота на угол матрица поворота на угол 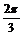 будет иметь вид будет иметь вид 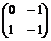 (тогда все матрицы в случае группы порядка 3), а если (тогда все матрицы в случае группы порядка 3), а если  повернут относительно повернут относительно 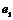 на угол на угол 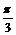 , то матрица поворота на угол , то матрица поворота на угол 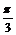 имеет вид имеет вид 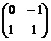 (тогда все матрицы в случае группы порядка 6 будут целочисленные). (тогда все матрицы в случае группы порядка 6 будут целочисленные). 
Теорема. Пусть 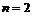 и и 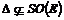 , т.е. в , т.е. в 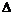 есть несобственное преобразование (преобразование с определителем есть несобственное преобразование (преобразование с определителем 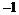 ), тогда ), тогда 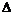 - одна из следующих групп: - одна из следующих групп:
1)  , ,
2) 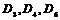 , ,
3) циклическая группа порядка 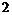 . .
Доказательство.
Пусть 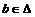 и и 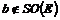 . Если . Если  и и 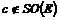 , тогда , тогда  . . 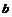 - это отражение относительно некоторой оси, следовательно матрица - это отражение относительно некоторой оси, следовательно матрица 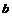 в некотором базисе имеет вид в некотором базисе имеет вид 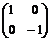 , но в любом базисе имеем , но в любом базисе имеем 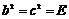 . .
Имеем, что 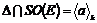 , где , где  . . 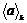 - подгруппа индекса 2 в - подгруппа индекса 2 в 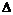 , следовательно , следовательно 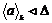 и и  . Т.к. . Т.к. 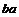 - это снова симметрия относительно некоторой оси, то - это снова симметрия относительно некоторой оси, то  и и 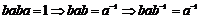 , т.к. , т.к.  . Следовательно группа . Следовательно группа  - это группа диэдра. - это группа диэдра.
В случае  эта группа превращается в группу эта группа превращается в группу 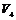 . .
В случае 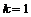 это циклическая группа порядка 2. это циклическая группа порядка 2. 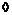
Покажем теперь, как можно получить все эти варианты групп 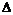 (пусть (пусть  - базис): - базис):
1) если 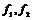 не перпендикулярны и имеют разные длины, то не перпендикулярны и имеют разные длины, то  , где , где 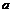 - центральная симметрия; - центральная симметрия;
2) если 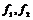 перпендикулярны и имеют разные длины, то перпендикулярны и имеют разные длины, то 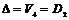 ; ;
3) если 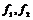 перпендикулярны и имеют одинаковые длины, то перпендикулярны и имеют одинаковые длины, то 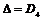 ; ;
4) если 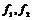 не перпендикулярны, имеют равные длины и не образуют правильный треугольник, то не перпендикулярны, имеют равные длины и не образуют правильный треугольник, то 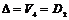 ; ;
5) если 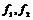 образуют правильные треугольник, то образуют правильные треугольник, то 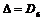 . .
6) также допустимы подгруппы этих групп, таким образом, получаются все указанные нами группы.
Двумерный случай разобран полностью. Есть также теорема, утверждающая, что порядок конечной подгруппы в группе ортогональных матриц ограничен для каждого 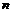 числом числом  (в случае (в случае 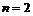 имеем имеем 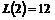 ), т.е. таких групп ), т.е. таких групп 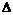 конечное число для любого конечное число для любого 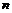 . .
Приведем описание (без доказательства) трехмерного случая:
Пусть 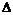 - конечная подгруппа в - конечная подгруппа в 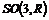 , тогда , тогда  - это: - это:
1) циклическая группа порядка  ; ;
2) 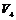 ; ;
3)  ; ;
4) 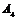 ; ;
5)  ; ;
6)  . .
|