|
Коэффициент внутреннего трения (вязкости) для газа может быть найден из формулы Пуазейля:
 , (1) , (1)
где  - радиус капилляра, - радиус капилляра,
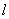 - его длина, - его длина,
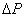 - разность давлений на концах капилляра, которой обусловлено течение газа, - разность давлений на концах капилляра, которой обусловлено течение газа,
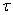 - время, в течение которого протекает объем газа, равный V. - время, в течение которого протекает объем газа, равный V.
Так как все величины в правой части формулы (1) доступны измерению, то этой формулой можно непосредственно пользоваться для определения коэффициента внутреннего трения газа.
С другой стороны, кинетическая теория устанавливает определенное соотношение между коэффициентом внутреннего трения газов, средней длиной свободного пробега молекул газа и средней скоростью их движения. Это соотношение обыкновенно пишут в таком виде:
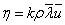 (2) (2)
где r - плотность газа,
 - средняя длина свободного пробега газовых - средняя длина свободного пробега газовых
молекул,
 - средняя (арифметическая) скорость их движения. - средняя (арифметическая) скорость их движения.
Численное значение коэффициента k зависит от сил взаимодействия между молекулами газа и приближенно равняет 0,5. Таким образом, формула (2) принимает вид:
 . (3) . (3)
Если известна температура газа, при которой определялся коэффициент внутреннего трения h, то средняя скорость газовых молекул  может быть найдена по известному выражению: может быть найдена по известному выражению:
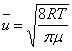 , (4) , (4)
где R - универсальная газовая постоянная,
Т - абсолютная температура газа,
m - молекулярный вес.
Плотность r газа берется при тех условиях (давлении и температуре) , при которых определялось  , и определяется из уравнения Клапейрона: , и определяется из уравнения Клапейрона:
 . (5) . (5)
И из формулы (3) можно найти длину свободного пробега.
Известное соотношение
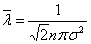 (6) (6)
позволяет найти эффективный диаметр молекул газа, если известно  . .
n - Число молекул газа n при данных условиях (температуре и давлении) в единице объема.
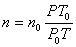 , ,
где  - число молекул в 1 - число молекул в 1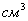 при нормальных условиях (число Лошмидта). при нормальных условиях (число Лошмидта).
Таким образом, измерив коэффициент вязкости газа, можно найти длину свободного пробега и эффективный диаметр его молекул
Выполнение работы
Сосуд A (см. рис.) с краном в нижней части наполнен водой так, чтобы уровень воды не выходил за пределы шкалы S, укрепленной на сосуде. Капилляр K находится в цилиндре C, который закрыт сверху и имеет оливки для впуска пара, если измерения производятся при температуре паров кипящей воды.
Капилляр соединен со змеевиком сравнительно большого диаметра, один конец которого q выходит наружу, через него газ поступает в капилляр.
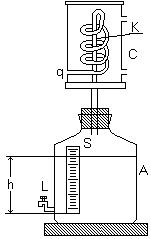
Если открыть кран L, то вода будет выливаться из сосуда, а через капилляр воздух будет засасываться в него. При этом следует иметь в виду, что правильные результаты опыта будут в том случае, если истечение воды определяется диаметром капилляра K, а не отверстием крана L.
Для определения коэффициента вязкости нужно знать 
Радиус капилляра r измеряют на отрезанном от него кусочке микроскопом. Измерения следует производить несколько раз в разных направлениях, после чего вычисляют среднее значение. Давление 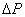 , под которым втекает воздух в капилляр, V и , под которым втекает воздух в капилляр, V и 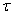 находят таким образом. Если открыть кран L, то сначала вода из него выливается непрерывной струйкой благодаря некоторому избыточному давлению над поверхностью воды в сосуде, но скоро она начинает вытекать сериями капель, так как капилляр узкий и воздух просачивается через него медленно. Пустой стаканчик, предварительно перед этим взвешенный, подставляют после какой-то очередной серии капель и одновременно пускают секундомер. Сразу же замечают по шкале S высоту уровня воды находят таким образом. Если открыть кран L, то сначала вода из него выливается непрерывной струйкой благодаря некоторому избыточному давлению над поверхностью воды в сосуде, но скоро она начинает вытекать сериями капель, так как капилляр узкий и воздух просачивается через него медленно. Пустой стаканчик, предварительно перед этим взвешенный, подставляют после какой-то очередной серии капель и одновременно пускают секундомер. Сразу же замечают по шкале S высоту уровня воды 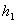 . Когда в стаканчике будет приблизительно 50-70 . Когда в стаканчике будет приблизительно 50-70  воды, его убирают, секундомер останавливают и замечают новый уровень воды в сосуде воды, его убирают, секундомер останавливают и замечают новый уровень воды в сосуде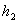 . По весу воды в стаканчике находят объем воздуха, вошедшего через капилляр в сосуд, то есть V . . По весу воды в стаканчике находят объем воздуха, вошедшего через капилляр в сосуд, то есть V .
Давление, под которым втекает воздух в сосуд, будет

По полученным данным находят h. Затем, измерив комнатную температуру и барометрическое давление воздуха, определяют 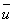 и r и находят и r и находят  , а затем уже s. Такой же опыт проделывают при температуре паров кипящей воды, пропуская через цилиндр C пар от кипятильника. , а затем уже s. Такой же опыт проделывают при температуре паров кипящей воды, пропуская через цилиндр C пар от кипятильника.
Измерение начинают через несколько минут после того, как пар начал выходить из оливки.
|

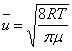 , (4)
, (4) 









