|
Если в некотором объеме имеется неоднородная смесь газов (при одинаковых по всему объему давлении и температуре), то тепловое движение перемешивает их, пока повсюду не образуется однородная смесь молекул, в которой парциальное давление и плотность каждого газа будут одинаковыми во всех частях объема. Этот процесс выравнивания концентраций называется диффузией.
Рассмотрим одномерный случай, когда плотность диффундирующего газа зависит от одной лишь координаты (обозначим её х ), и плоскости, перпендикулярные оси ОХ , являются плоскостями равных концентраций. Тогда количество вещества dМ, перенесенное через какую-нибудь площадку S, перпендикулярную оси ОХ за время d t равно
 где где 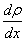 - градиент плотности при - градиент плотности при 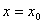
D - коэффициент диффузии, который численно равен количеству вещества, переносимого через единичную площадку за единицу времени при единичном градиенте плотности.
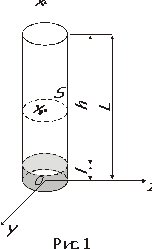
В общем случае D зависит от концентрации газов, однако при малой концентрации одного из газов, коэффициент диффузии можно считать постоянным, т.е. независимым от  . Для определения коэффициента диффузии паров жидкости в воздухе при малых концентрациях паров применяется следующий метод: жидкость наливается на дно длинной узкой ампулки, укрепленной на чашке магнитных весов. Испаряющиеся с поверхности молекулы жидкости диффузионным путем (если отсутствует перемешивание газа) удаляются из ампулки. Будем исходить из предположения, что над поверхностью жидкости находится насыщенный пар. У краев ампулки концентрация молекул равна нулю. . Для определения коэффициента диффузии паров жидкости в воздухе при малых концентрациях паров применяется следующий метод: жидкость наливается на дно длинной узкой ампулки, укрепленной на чашке магнитных весов. Испаряющиеся с поверхности молекулы жидкости диффузионным путем (если отсутствует перемешивание газа) удаляются из ампулки. Будем исходить из предположения, что над поверхностью жидкости находится насыщенный пар. У краев ампулки концентрация молекул равна нулю.
Чем выше ампулка, тем вероятнее первое предположение. При большой высоте h градиент плотности паров мал. В связи с этим диффузионный поток невелик, то есть сравнительно мало молекул пара отводится путем диффузии от поверхности жидкости. В результате процесс испарения будет успевать поставлять в пар столько молекул, что над поверхностью жидкости будет насыщенный пар. Давление его  соответствует температуре Т, при которой проводится эксперимент, и определяется по графику зависимости соответствует температуре Т, при которой проводится эксперимент, и определяется по графику зависимости  (Т). Что касается второго предположения, то оно тем вероятнее, чем выше и уже ампулка, так как из высокой и узкой ампулки в единицу времени выходит незначительное количество паров жидкости, не создающее заметных концентраций в большом объеме, окружающем ампулку. (Т). Что касается второго предположения, то оно тем вероятнее, чем выше и уже ампулка, так как из высокой и узкой ампулки в единицу времени выходит незначительное количество паров жидкости, не создающее заметных концентраций в большом объеме, окружающем ампулку.
При выполнении этих предположений коэффициент диффузии может быть легко определен. Через некоторое время после помещения ампулки на чашу весов установится постоянный диффузионный поток молекул жидкости, уходящих из ампулки. Взвешивая ее через определенные промежутки времени (5-10 мин.), получаем зависимость изменения массы жидкости  от времени t, зависимость, которая при установившемся процессе в координатах от времени t, зависимость, которая при установившемся процессе в координатах 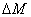 от t изображается прямой. Из наклона прямой определяем D, пользуясь формулой от t изображается прямой. Из наклона прямой определяем D, пользуясь формулой

где S – площадь сечения ампулки,
h – расстояние от поверхности жидкости до краев
ампулки,
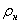 - плотность насыщенных паров, которая находится по формуле: - плотность насыщенных паров, которая находится по формуле:

где  - молекулярный вес жидкости, - молекулярный вес жидкости,
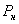 - давление насыщенных паров жидкости при - давление насыщенных паров жидкости при
температуре Т.
Размеры ампулки могут быть подобны экспериментальным путем. Высота, например, выбирается следующим образом: измеряем D при разных расстояниях h от поверхности жидкости до края ампулки. Начиная с некоторого значения 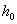 , D перестает зависеть от h. Для эксперимента, следовательно, можно пользоваться ампулкой, для которой , D перестает зависеть от h. Для эксперимента, следовательно, можно пользоваться ампулкой, для которой 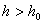 . С другой стороны, следует помнить, что чем больше высота и меньше диаметр ампулки, тем меньше изменение в массе, поэтому увеличивать высоту и уменьшать диаметр надо в таких пределах, чтобы изменение в массе было не слишком мало. . С другой стороны, следует помнить, что чем больше высота и меньше диаметр ампулки, тем меньше изменение в массе, поэтому увеличивать высоту и уменьшать диаметр надо в таких пределах, чтобы изменение в массе было не слишком мало.
Опыт следует производить при постоянной температуре, поскольку D=D(Т), и избегать конвекции в газе, что достигается плавным взвешиванием на магнитных весах и предохранением установки от толчков.
Выполнение работы
Закрытая ампулка с испытуемой жидкостью ставится на правую чашку весов и уравновешивается с помощью разновесов. Снимаем крышку с ампулки и кладем её на ту же чашку. Изменение массы ампулки с жидкостью в результате диффузии уравновешивается в дальнейшем с помощью последовательно соединенных катушек - соленоидов, через которые пропускается ток. Магнитные поля катушек направлены в одну и ту же сторону, что приводит к их взаимному отталкиванию. Имеющаяся градуировочная кривая m(мг), I(мA) позволяет определить изменение массы жидкости, соответствующее различным токам через катушки. Работу следует проводить при постоянно включенном токе с тем, чтобы избежать колебаний чашек весов.
Если ампулка непрозрачна, h следует определять так: взвешивается пустая ампулка и ампулка с жидкостью. Разность масс
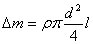
где - плотность жидкости, - плотность жидкости,
 – диаметр (внутренний) ампулки, – диаметр (внутренний) ампулки,
 – высота жидкости. – высота жидкости.
Если L – длина ампулки, то h=L-l.

рис.2
|












