Общие сведения. Взамкнутом контуре (рис. 10.3.1) после отключении его от источника постоянного или переменного напряжения могут возникнуть затухающие синусоидальные

Взамкнутом контуре (рис. 10.3.1) после отключении его от источника постоянного или переменного напряжения могут возникнуть затухающие синусоидальные колебания, обусловленные начальным запасом энергии в электрическом поле конденсатора и в магнитном поле катушки индуктивности.

В общем случае состояние цепи определяется из дифференциального уравнения, составленного по второму закону Кирхгофа:

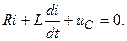
Поскольку 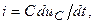то

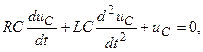
или

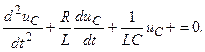
Рис. 10.3.1.

Вид решения этого дифференциального уравнения зависит от характера корней характеристического уравнения:

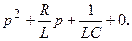
Корни этого уравнения:

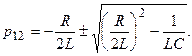
Когда 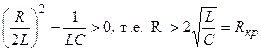, корни вещественные отрицательные и процесс изменения тока и напряжений имеет апериодический затухающий характер (рис.10.3.2а). Если же R<R_кр,то возникает колебательный процесс (рис. 10.3.2б). Тогда решение дифференциального уравнения имеет вид:

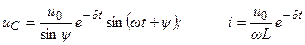sin wt,

где , .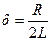

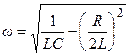Рис. 10.3.2.

При уменьшении сопротивления от некоторого значения большего, чем Rкр сначала увеличивается скорость затухающего апериодического процесса, затем, при R=Rкр качественно изменяется характер процесса – он становится колебательным - и при дальнейшем уменьшении сопротивления увеличивается частота колебаний и уменьшается затухание. При R, стремящемся к нулю, частота стремится к резонансной частоте 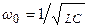, а затухание d – к нулю.

В данной работе заряд конденсатора до напряжения u₀ осуществляется однополярными прямоугольными импульсами напряжения и исследуется процесс его разряда на сопротивление и индуктивность во время пауз между импульсами. Повторяющийся процесс заряда и разряда конденсатора можно наблюдать на электронном или виртуальном осциллографе.