Дрейфовые и диффузионные токи в полупроводнике

Как было показано в лекции № 1, проводимость полупроводника определяется двумя составляющими: электронной и дырочной проводимостями. В общем случае перемещение носителей (электронов и дырок) может происходить за счет наличия электрического поля, напряженность которого 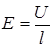, где U – напряжение, приложенное к полупроводнику; l – длина полупроводника; а также за счет наличия градиенты концентрации носителей по длине полупроводника. В первом случае ток называется дрейфовым, а во втором – диффузионным. Тогда

,

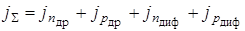где 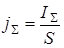А/см² – плотность тока в полупроводнике; – плотность дрейфового тока, вызванная перемещением электронов и дырок; 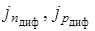– плотность диффузионного тока, вызванная перемещением электронов и дырок.

Величина плотности дрейфового тока зависит от скорости перемещения носителей заряда в полупроводнике 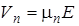и 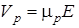, где m _n – коэффициент пропорциональности, который носит название подвижности электронов 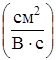, численно равен средней скорости перемещения электрона под действием электрического поля напряженностью 1 В/см; 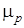– коэффициент пропорциональности, который носит название подвижности дырок. Подвижность электронов выше, чем дырок, поэтому при одинаковой плотности электронов и дырок (например, собственный полупроводник 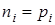) электронный ток дрейфовый больше дырочного.

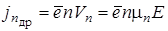, (1.7)

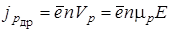, (1.8)

где 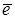– заряд электрона (1,6×10^-9 Кл); n – концентрация электронов; р – концентрация дырок.

Удельная электропроводность, вызванная дрейфовой составляющей

,

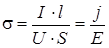где I – ток, протекающий через полупроводник; S – сечение полупроводника; 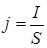– плотность тока; U – напряжение, приложенное к полупроводнику; l – длина полупроводника.

Тогда из (1.7) и (1.8) получим

, .

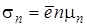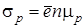Полная электропроводность, вызванная дрейфовой составляющей тока

,

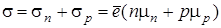а для собственных полупроводников, учитывая, что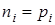

.

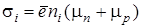Для нахождения диффузионных составляющих плотности тока 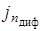и 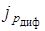, вместо градиента электрического потенциала 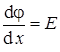, воспользуется градиентом химического потенциала, равного 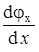, где dj – производная электрического потенциала; dj_x – производная химического потенциала; х – ось, совпадающая с направлением изменения концентрации.

В уравнениях (1.5) и (1.6) 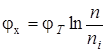для п -полупроводника и 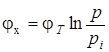для р -полупроводника. Тогда считая, что n_i и p_i = const,

, .

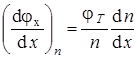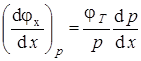Подставив эти значения в (1.7) и (1.8), получим

, .

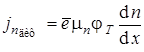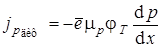Знак минус учитывает то, что движение носителей как электронов, так и дырок, всегда направлено в сторону уменьшения концентрации, а знак заряда у них разный.

Произведение 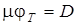называется коэффициентом диффузии, тогда

, .

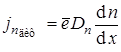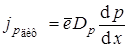Сравнивая составляющие дрейфовой и диффузионной плотностей токов, можно сделать вывод, что дрейфовый ток зависит от величины концентрации, а диффузионный – только от их градиента.

Полная плотность тока в полупроводнике

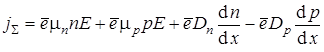. (1.9)