В том случае, когда необходимо определить ток в какой-либо ветви без определения токов в других ветвях, применяется метод активного двухполюсника и эквивалентного генератора.
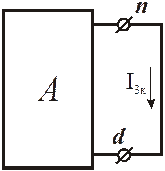
Ветвь, в которой необходимо определить ток, выделяется, а вся остальная схема заменяется активным двухполюсником. Так, схема (рис. 10) преобразуется следующим образом (рис. 11):
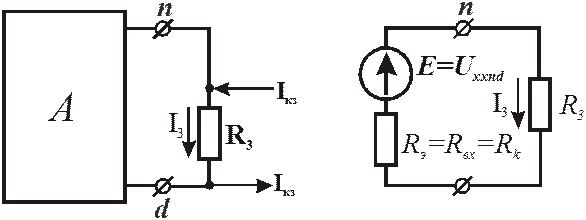
Активный двухполюсник может быть заменён эквивалентным генератором напряжения с ЭДС Е, равной напряжению холостого хода 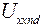 на зажимах разомкнутой выделенной ветви nd и внутренним сопротивлением
на зажимах разомкнутой выделенной ветви nd и внутренним сопротивлением 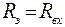 , равным входному сопротивлению пассивного двухполюсника относительно зажимов " n " и " d ".
, равным входному сопротивлению пассивного двухполюсника относительно зажимов " n " и " d ".
Напряжение холостого хода 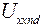 берётся в направлении тока
берётся в направлении тока 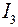 выделенной ветви в исходной схеме, т.е. от узла n к узлу d (
выделенной ветви в исходной схеме, т.е. от узла n к узлу d (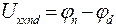 ). Причём это напряжение холостого хода
). Причём это напряжение холостого хода 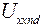 определяется по схеме рис. 14, которая получается, если в выделенной ветви осуществить режим холостого хода введением разомкнутого ключа К.
определяется по схеме рис. 14, которая получается, если в выделенной ветви осуществить режим холостого хода введением разомкнутого ключа К.
Тогда ток 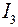 в выделенной ветви определяется по формуле:
в выделенной ветви определяется по формуле:
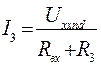 . (46)
. (46)
Внутреннее сопротивление эквивалентного генератора может быть вычислено двумя способами:
1) непосредственно по схеме, для чего активный двухполюсник преобразуется в пассивный. Идеальные источники ЭДС, имеющиеся в активном двухполюснике, закорачиваются, а ветви с источником тока размыкаются; вместо реальных источников в пассивной схеме должны оставаться их внутренние сопротивления;
2) по формуле:
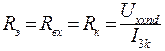 , (47)
, (47)

 где
где  ток короткого замыкания выделенной ветви nd (рис. 13) который может быть вычислен при закорачивании зажимов n и d, если схема активного двухполюсника известна, либо определён опытным путем. Напряжение холостого хода также может быть определено любым методом расчёта линейных электрических цепей или найдено опытным путём.
ток короткого замыкания выделенной ветви nd (рис. 13) который может быть вычислен при закорачивании зажимов n и d, если схема активного двухполюсника известна, либо определён опытным путем. Напряжение холостого хода также может быть определено любым методом расчёта линейных электрических цепей или найдено опытным путём.
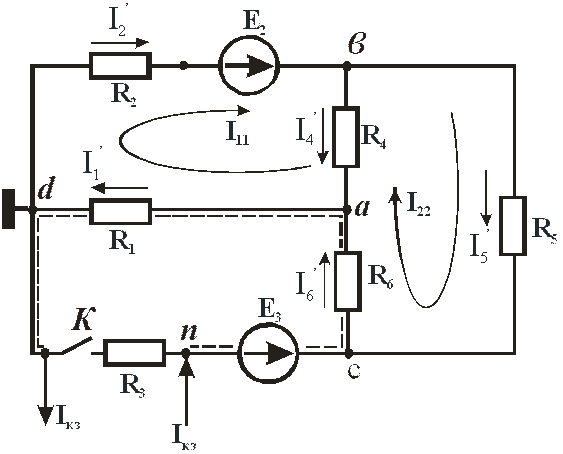
Разомкнём ветвь nd в заданной схеме. Получим новую схему (рис. 14), в которой четыре узла: а, в, с, d (У=4) и пять ветвей (В=5): ав, ас, аd, сd, вd.
По первому закону Кирхгофа можно составить К1=У-1=3 уравнения, по второму закону Кирхгофа К2=В-(У-1)=5-3=2 уравнения.
Если эту схему рассчитывать методом узловых потенциалов, то придётся составить схему из трёх узловых уравнений.
|
Если же схему рассчитывать методом контурных токов, то надо будет составить систему из двух контурных уравнений.
Очевидно, что в данном случае использование метода контурных токов дает некоторую экономию времени расчёта.
Исходя из этих соображений, определим напряжение холостого хода  на зажимах разомкнутой ветви nd методом контурных токов.
на зажимах разомкнутой ветви nd методом контурных токов.
В схеме на рис. 14 выберем произвольно направления токов в ветвях и выберем два независимых контурах авdа и авса.
Контурные токи 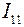 и
и 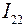 направим по часовой стрелке в соответствующих контурах авdа и авса.
направим по часовой стрелке в соответствующих контурах авdа и авса.
Решим систему уравнений:
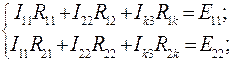 (48)
(48)
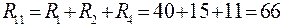
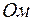 ;
;
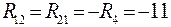
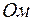 ;
;
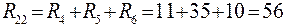
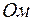 ;
;
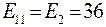
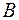 ;
;
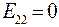
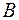 .
.
Условимся, что в схеме рис. 14 ток 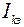 от источника тока проходит по контуру nсаd. Тогда сопротивление
от источника тока проходит по контуру nсаd. Тогда сопротивление 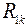 первого контура, по которому проходит ток от источника тока будет равно
первого контура, по которому проходит ток от источника тока будет равно
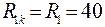
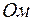 .
.
Сопротивление 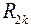 , второго контура, по которому проходит ток от источника тока
, второго контура, по которому проходит ток от источника тока
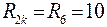
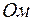 .
.
Сопротивления 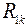 и
и 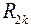 взяты положительными, так как направления контурных токов
взяты положительными, так как направления контурных токов 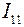 и
и 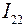 совпадают с током
совпадают с током 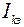 от источника тока.
от источника тока.
После подстановки численных значений система уравнений примет вид
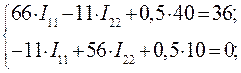
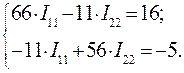
Решаем эту систему уравнений:
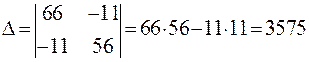
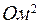 ;
;
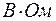 ;
;
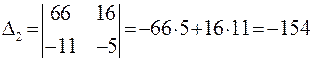
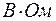 ;
;
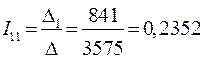
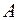 ;
;
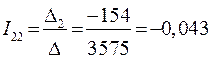
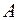 .
.
Находим токи в схеме по контурным токам:
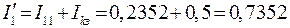
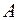 ;
;
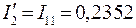
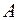 ;
;
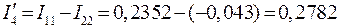
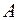 ;
;
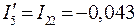
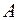 ;
;
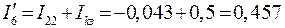
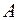 .
.
Токи в схеме рис. 14 рассчитаны правильно, так как подстановка токов 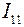 и
и 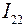 в систему уравнений (48) даёт тождества
в систему уравнений (48) даёт тождества
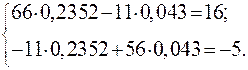
Примем за нуль потенциал точки d: 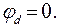
Тогда:
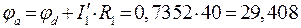
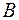 ;
;
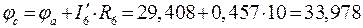
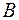 ;
;
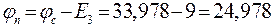
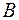 .
.
Напряжение холостого хода 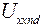 па на зажимах разомкнутой ветви равно:
па на зажимах разомкнутой ветви равно:
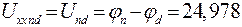
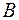 .
.
Находим входное сопротивление пассивного двухполюсника относительно зажимов n и d. Преобразуем схему рис. 14 в пассивный двухполюсник, для чего закорачиваем источники ЭДС Е2 и Е3 и размыкаем ветвь с источником тока 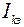 . По определению, сопротивление источника тока равно бесконечности, что эквивалентно размыканию ветви с источником тока. Поэтому эта ветвь не будет участвовать в преобразованиях схемы.
. По определению, сопротивление источника тока равно бесконечности, что эквивалентно размыканию ветви с источником тока. Поэтому эта ветвь не будет участвовать в преобразованиях схемы.
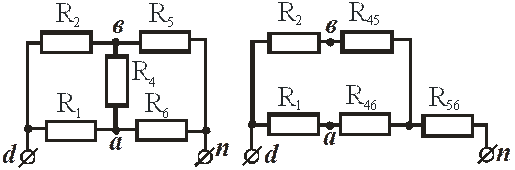
В схеме рис. 15 можно преобразовать звезду резисторов R2, R4, R5 в эквивалентный треугольник или же любой из треугольников резисторов R1, R4, R2 и R4, R5, R6 в эквивалентную звезду. Указанные преобразования равноправны. Преобразуем треугольник резисторов R4, R5, R6 в эквивалентную звезду R45, R46, R56 (рис. 16).
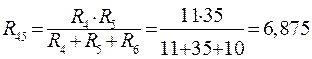
 ; (49)
; (49)
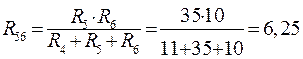
 ; (50)
; (50)
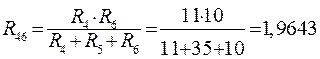
 . (51)
. (51)
По схеме рис. 16 находим входное сопротивление пассивного двухполюсника:
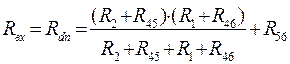 ;
;
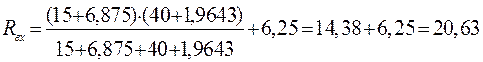
 .
.
Рассчитаем ток 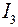 :
:
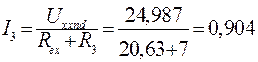
 .
.
Как видим, величина тока 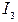 точно совпадает с расчётными значениями, определёнными методом контурных токов и методом узловых потенциалов.
точно совпадает с расчётными значениями, определёнными методом контурных токов и методом узловых потенциалов.
 2015-05-26
2015-05-26 9582
9582
