3. Средние параметры определяются по первой гармонике. Для их у0 определения на нелинейный элемент подают гармоническое колебание x(t) =Х т сos 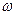 t, из спектра реакции
t, из спектра реакции
выделяют первую гармонику Уm1 Х
Xcos(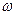 t +
t + 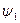 ), и делят комплексную амплитуду реакции на амплитуду воздействия
), и делят комплексную амплитуду реакции на амплитуду воздействия
а ср = (Ут1/Х т)ej 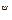
Средние параметры не могут быть определены графически, обычно их находят аналитически, располагая математическим выражением для внешней характеристики.
В радиотехнике широко применяется понятие ср едней крутизны ВАХ лампы, транзистора. Эта величина определяется как отношение амплитуды первой гармоники выходного тока камплитуде входного гармонического напряжения
S ср. = Im1/Um (4.5) Понятие средней крутизны означает, что за время одного периода подведенного напряжения ВАХ считается линейной с наклоном S ср
Пример 4.1. Экспериментально снятые ВАХ диодов заданы графиками на рис. 4.4. Определить статические и дифференциальные параметры диодов (проводимость, сопротивление) при напряжении U0= 1,0 В.
При заданном напряжении U0= 1,0 В определяем рабочую точку и проводим в ней касательную к ВАХ для определения угла между касательной и осью абсцисс. Для полупроводникового диода (рис. 4.4, а) в рабочей точке (U0=1,0 В, l0=6,0 мА параметры будут равны: G(1,0) =I0/ U0 =60 1,0-3/1,0 =6,0.10-3 См, R(1,0) =1/G(1,0) =166,7 Ом, Gдиф(1,0) =10 /(U0 –U1) =6 10-3/ (1,0 — 0,5) =1,2.10-2 См, Rдиф(1,0) =83,3 Ом.
Для туннельного диода (рис. 4.4,6) в рабочей точке U0 =1,0 В, Iо=2,5 мА параметры вычисляются аналогично: G(1,0) =2,5 10-3/1,0=2,5 10-2 См. R(1,0) =400 Ом, Gдиф(1,0) =2,5.10-2 /(1,0 — 2,0) = — 2,5.10-2 См, Rдиф (1,0) = — 400 Ом.
Обращает внимание тот факт, что для туннельного диода дифференциальная проводимость и сопротивление отрицательны. И это не случайно, так как рабочая точка находится на падающем участке вольт-амперной характеристики, где положительному приращению напряжения соответствует отрицательное приращение тока.
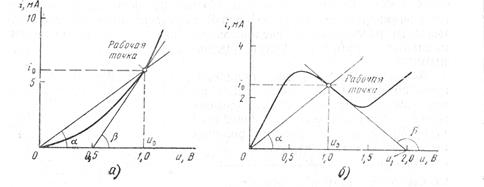
Рис. 4.4. Статические характеристики диодов: а – полупроводникового; б – туннельного.
Физический смысл отрицательного сопротивления. Отрицательным в нелинейном резисторе может быть только дифференциальное сопротивление, статическое сопротивление всегда положительно. Из определения дифференциального
сопротивления (4.5) следует, что оно представляет собой сопротивление нелинейного резистора переменному току малой амплитуды. Отрицательный знак Rдиф означает, что напряжение на резисторе и ток через него противофазны, поэтому и средняя мощность, потребляемая резистором, отрицательна, а отрицательную мощность имеют только источники ЭДС.
Итак, положительное дифференциальное сопротивление является потребителем, а отрицательное — источником энергии переменного тока.
Инерционные нелинейные элементы. Инерционность НЭ следует рассматривать в электрическом и тепловом смыслах.
Инерционным в электрическом смысле является такой НЭ, в котором фаза первой гармоники отклика отстает от фазы гармонического воздействия. В диодах, транзисторах, электронных лампах инерционность проявляется на СВЧ, где из-за инерционности электронов ток не успевает следить за изменением напряжения на электродах. Инерционность учитывают в эквивалентной схеме включением реактивных элементов L и С. Реактивные НЭ (индуктивности, конденсаторы) являются инерционными по своей
сущности, так как способны накапливать электрическую энергию.
К инерционным в тепловом смысле нелинейным элементам относятся термосопротивления (термисторы), сопротивление которых зависит от температуры и соответственно тока, протекающего через него. Заметим, что при питании термистора переменным током вследствие тепловой инерции характерна линейная зависимость между мгновенными значениями тока и напряжения и. нелинейная зависимость между действующими значениями.
4.3. АППРОКСИМАЦИЯ НЕЛИНЕЙНЫХ
ХАРАКТЕРИСТИК
Задача аппроксимации. Как правило, внешние характеристики НЭ получают экспериментально, располагая весьма несложной аппаратурой. Предприятия-изготовители НЭ снабжают их типовыми статическими характеристиками. Расчеты по этим
характеристикам можно проводить графическим способом, который громоздок и весьма неточен.
Для аналитических расчетов необходимо иметь математическое выражение статических характеристик НЭ, т. е. статическая характеристика должна быть выражена с помощью какой-то функции. Поэтому возникает задача аппроксимации — подбора такой функции, которая, будучи достаточно простой, отражала бы важнейшие особенности экспериментально снятой характеристики.
Процедура аппроксимации состоит из трех этапов: выбора аппроксимирующей функции, определения ее коэффициентов и проверки точности аппроксимации. Для упрощения обычно аппроксимируют не всю характеристику НЭ, а только ее рабочий участок, под которым понимается используемая часть характеристики. В радиотехнике и электросвязи чаще всего применяются два способа аппроксимации: кусочно-линейный и полиномиальный.
Кусочно-линейная аппроксимация. Суть способа состоит в замене реальной характеристики отрезками прямых линий с различными наклонами. Этот способ является довольно грубым, но при больших амплитудах внешних воздействий он дает
вполне удовлетворительные результаты. Способ получил широкое распространение в инженерной практике при расчетах умножителей частоты, усилении мощных колебаний, детектировании, выпрямлении и т. д.
На рис. 4.5 показана статическая характеристика выпрямительного диода КД103, аппроксимированная двумя отрезками прямых
i(u) = 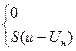 1) при u < U н; 2) при и
1) при u < U н; 2) при и 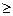 U н (4.6)
U н (4.6)
где Uн=0,5 В — напряжение начала характеристики; S=80 мА/В—крутизна тока диода.
Необходимо отметить, что кусочно-линейная аппроксимация не может быть использована при изучении процессов, связанных с изменением крутизны характеристики: генерирования колебаний, квадратичного детектирования и др.
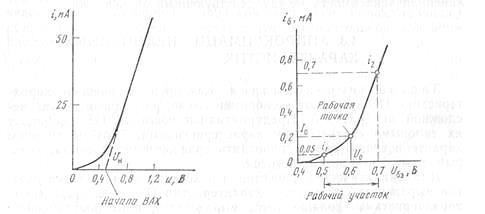
Рис. 4.5. Статистическая характеристика Рис. 4.6. Полномиальная аппроксимация
диода КД103 и её кусочно-линейная входной характеристики транзистора КТЗ102
аппроксимация
Полиномиальная аппроксимация. Кривую любого вида можно представить в виде степенного полинома относительно рабочей точки х0, у0:
у — у0=а1(х — х0)+а2(х — хо)2+... +ап(х — хп)п. (4.7)
Здесь коэффициенты а0, а1,...,ап — вещественные числа. Число членов разложения определяется требуемой точностью расчетов.
Из множества методов нахождения коэффициентов наиболее общим является метод выбранных точек. На характеристике в пределах рабочего участка выбирают точки, число которых равно числу коэффициентов и. Координаты этих точек y0=a0, x1, y1; x2, у2,., хп, уп, найденные из заданной характеристики НЭ, поочередно подставляют в аппроксимирующий полипом (4.7) и получают систему из и уравнений с и неизвестными. Решая систему, находим коэффициенты. Указанный метод иллюстрируется примером 4.2.
Пример 4.2. На рис. 4.6 изображена входная ВАХ транзистора КТ3102,
на базу которого подано напряжение u(t) = Uo+Um sin 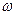 t =0,6+0,1 sin
t =0,6+0,1 sin 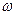 t, В.
t, В.
Требуется аппроксимировать заданную характеристику относительной рабочей
точки полиномом второй степени.
Рабочая точка определяется постоянным смещением Uo = 0,6 В. Рабочий
участок характеристики простирается от Uo — Um,=0,6 — 0,1=0,5 В до Uo+Um=
=0,6+0,1=0,7 В. В качестве точек аппроксимации выбираем точки на краях рабочего участка (на графике отмечены кружками). Значения тока в выбранных точках: i1 =0,05 мА; i р.т.=I0=0,2 мА; i2 =0,7 мА.
Исходя из (4.7), составляем уравнения для выбранных точек 1 и 2
i1— Io= a1 (u1 - Uo) +a2 (u1 — Uо) 2;
i2 — Io = a1 (u2 — Uo) + a2 (u2 — Uo)2.
Подставляя числовые значения токов и напряжений, получим систему линейных равенств
— 0,15 = — 0,1 a1 +0,01 a2;
0,5 = 0,1 а1 +0,01 a2
откуда а1=3,25 мА/В, a2=17,5 мА/В2. Аппроксимирующий полипом будет иметь
вид: i — 0,2=3,25(u — 0,6)+17,5(и — 0,6)2, мА.
4.4. ВОЗДЕЙСТВИЕ ГАРМОНИЧЕСКОГО
КОЛЕБАНИЯ НА БЕЗЫНЕРЦИОННЫЙ
НЕЛИНЕЙНЫЙ ЭЛЕМЕНТ
Форма реакции. Пусть на НЭ с внешней характеристикой у= f (х) воздействует гармоническое колебание х(t) =Хm+Xcos 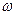 t. Форму реакции можно найти графическим или аналитическим методами.
t. Форму реакции можно найти графическим или аналитическим методами.
Графический метод называют еще методом проекций. Он основан на построении третьей проекции y(t) (реакции НЭ) по известным двум: воздействию х(t) и характеристике y=f(x). Эти
Рис. 4.7. Графическое построение кривой, отображающей реакцию безынерционной линейной цепи.
несложные построения проведены на рис. 4.7, где стрелками показано нанесение характерных точек 1... 7: максимумы, минимумы, пересечение с осью абсцисс. Промежуточные точки строятся аналогично. Из рис. 4.7 видно, что реакция у(t) является периодической, но существенно отличается от гармонического воздействия. Разлагая реакцию в ряд Фурье, получим, что она содержит постоянную составляющую, основную частоту в и набор гармоник 2 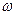 , З
, З 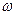 ,... Физическая природа искажения кривой реакции
,... Физическая природа искажения кривой реакции
простая: одинаковым приращениям воздействия соответствуют неодинаковые приращения реакции, поскольку крутизна характеристики разная. Нахождение амплитуд спектральных составляющих реакции Yo, Y1, Y2... является важнейшей задачей аналитического расчета нелинейной цепи. Решение производится по-разному, в зависимо-
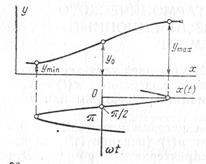 Рис. 4.8. Определение ординат реакции нелинейного элемента
Рис. 4.8. Определение ординат реакции нелинейного элемента
сти от вида аппроксимирующей функции.
Метод п ординат. Это rpaфоаналитический метод, не требующий аппроксимации характеристики НЭ. Метод позволяет определить и первых составляющих спектра реакции, полагая, что остальные достаточно малы. На практике применяются методы трех (n=3) и пяти (n=5) ординат. Так, по методу трех ординат считаем, что реакция содержит три составляющих у= Y0+ У1 cos 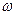 t+ У2, cos 2
t+ У2, cos 2 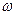 t. Задавая значения аргумента
t. Задавая значения аргумента 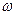 t=O,
t=O, 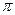 /2,
/2, 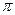 по характеристике НЭ (рис. 4.8), определяем соответствующие им значения уmax, у0, уmin реакции. В результате получаем систему уравнений
по характеристике НЭ (рис. 4.8), определяем соответствующие им значения уmax, у0, уmin реакции. В результате получаем систему уравнений
уmax = У0+ У1+ У2,
уо = У0+0 — У2,
уmin = У0- У1+ У2,
откуда
Y0 = 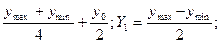
Y2 = 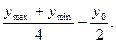


Аналогично, по методу пяти ординат в реакции определяем пять составляющих. Выбрав пять значений аргумента 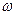 t =0
t =0 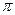 /3,
/3, 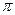 /2, 2
/2, 2 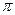 /3,
/3, 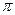 , получим систему уравнений, из которой находим коэффициенты ряда Фурье Уо, У1, У2, У3, У4.
, получим систему уравнений, из которой находим коэффициенты ряда Фурье Уо, У1, У2, У3, У4.
Метод угла отсечки. При этом методе используется кусочно-линейная аппроксимация характеристики НЭ. Форма реакции находится графическим методом проекций. Для НЭ с характеристикой (4.6)
y= 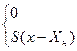 1) при x< Xн; 2) при x
1) при x< Xн; 2) при x 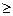 Xн
Xн

Рис. 4.9. Реакция НЭ с кусочно-линейной характеристикой.
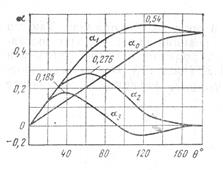 Рис.4.10. Графики первых четырёх функций Берга
Рис.4.10. Графики первых четырёх функций Берга
при гармоническом воздействии с постоянным смещением Х0 х(t) =Хо+Х cos 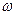 t графическое построение реакции y(t) показано на рис. 4.9.
t графическое построение реакции y(t) показано на рис. 4.9.
Форма реакции имеет характерный вид косинусоидальных импульсов с отсечкой. Полученные импульсы характеризуются двумя параметрами: высотой уmax и шириной 20. Половина времени существования импульса называется углом отсечки 0. Угол отсечки определяется из равенства X0+Xm соs 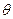 =Хн откуда cos
=Хн откуда cos 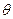 = (Хн — X0) /Xm. (4.8)
= (Хн — X0) /Xm. (4.8)
Высота (максимальное значение) импульса
Уmax = Sxmax = SXm (1-cos 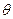 ).
).
Спектральный состав таких периодических косинусоидальных импульсов определяется по известным формулам ряда Фурье и подробно изучен советским ученым, академиком А. И. Бергом. Постоянная составляющая и амплитуды гармоник вычисляются
по выведенным им формулам
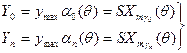 (4.9)
(4.9)
в которые входят функции Берга 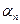 (
(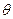 ) (рис. 4.10) или
) (рис. 4.10) или
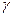 n(
n(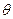 ) = (1 — cos
) = (1 — cos 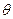 ) a (
) a (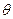 ) (4.10)
) (4.10)
Пример 4.3. На выпрямительный диод КД103, характеристика которого
изображена на рис. 4.5, приложено напряжение u(t) =0,4+0,8cos 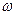 t, В. Вы-
t, В. Вы-
числить постоянную составляющую Iо и амплитуду первой гармоники Im1 протекающего тока.
Параметры аппроксимации диода были определены ранее (см. $ 4.3):
Uн =0,5 В; S=80 мА/В. Подставляя в формулу (4.8) Х0=U0=0,4 В; Хm=Um=
=0,8 В, получим соs 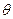 = (0,5 — 0,4)/0,8=0,125 и
= (0,5 — 0,4)/0,8=0,125 и 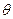 =агссоs 0,125=82,8o. Значение
=агссоs 0,125=82,8o. Значение
функций Берга определяем из рис. 4.10: a0 (82,8o) =0,29; а1 (82,8o) =0,49. По
формулам (4.9) и (4.10) находим Io =8,0* 0,8 (1 — 0,125).0,29=1624 мА; Im1 =
=80 *0,8 (1 — 0,125)* 0,49=27,44 мА.
4.5. ВОЗДЕЙСТВИЕ НА НЕЛИНЕЙНЫЙ
И ПАРАМЕТРИЧЕСКИЙ ЭЛЕМЕНТЫ
ПОЛИГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
Комбинационные частоты. Входное воздействие представляется тригонометрической суммой гармонических колебаний х(t) = 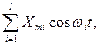
причем 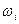 — произвольные частоты, не обязательно кратные; l —число гармонических колебаний воздействия. Требуется определить амплитуды, частоты, фазы всех спектральных составляющих реакции у(t). Решение этой задачи, как правило, приводит к громоздким математическим выкладкам. Но поскольку нелинейная (параметрическая) цепь преобразует спектр воздействия, реакцию y(t) можно представить в виде суммы постоянной Уо и гармонических составляющих с различными амплитудами Уmk, частотами
— произвольные частоты, не обязательно кратные; l —число гармонических колебаний воздействия. Требуется определить амплитуды, частоты, фазы всех спектральных составляющих реакции у(t). Решение этой задачи, как правило, приводит к громоздким математическим выкладкам. Но поскольку нелинейная (параметрическая) цепь преобразует спектр воздействия, реакцию y(t) можно представить в виде суммы постоянной Уо и гармонических составляющих с различными амплитудами Уmk, частотами 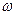 k, фазами
k, фазами 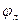 .
.
y (t) = Y0+ 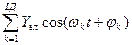 ,
,
которая в общем случае содержит как частоты воздействия, так и новые частоты. Физическая причина появления гармоник основных частот была приведена в $ 4.4. Кроме гармоник в спектре реакции появляются также всевозможные суммарные и разностные частоты, которые получили название комбинационных частот. Так, при воздействии двух гармонических колебаний на квадратичный нелинейный элемент (см. пример 4.4) в спектре реакции содержатся гармоники 2 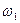 |, 2
|, 2 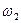 , суммарная
, суммарная 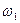 +
+ 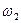 и разностная
и разностная 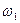 -
- 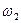 частоты. Всех этих частот в воздействии не было.
частоты. Всех этих частот в воздействии не было.
Пример 4.4. Определить реакцию НЭ с квадратичной ВАХ у=а2 x2 на воздействие x(t) =Xm1 cos 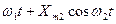
Для заданного воздействия реакция у= 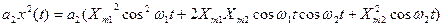 .
.
 Используя тригонометрические формы
Используя тригонометрические формы 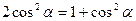 и
и 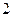
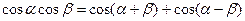 ,получаем
,получаем
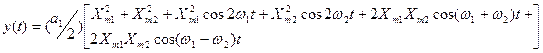
При увеличении числа частот воздействия l и степени аппроксимирующего полинома n число частот спектра реакции резко увеличивается и может исчисляться десятками и сотнями. Так, уже при l =2 и n =З в спектре реакции НЭ имеется двенадцать различных частот.
При изучении частоты реакции была замечена следующая закономерность: комбинационные частоты можно представить в виде
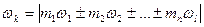 , (4.11)
, (4.11)
где mi — любые целые положительные числа, включая нуль. Для вычислений комбинационные частоты удобно группировать, объединяя вместе те частоты, для которых
m1+m2+…+mn= М, (4.12)
где М — порядок комбинационной частоты. Знак модуля в (4.11) поставлен для учета при вычислениях физически существующих положительных частот.
При составлении по выражениям (4.11) и (4.12) списка комбинационных частот следует учитывать важную закономерность: слагаемое со степенью и в полиномиальной аппроксимации характеристики НЭ вызывает появление комбинационных частот с максимальным порядком Mmax=n. При этом, если n — четное число, в реакции появляется постоянная составляющая, возникают гармоники и комбинационные частоты только четных порядков: М= 2, 4,..., n. Если n — нечетное число, то в спектре реакции содержатся частоты воздействия и порядок гармоник и комбинационных частот нечетный: M=3, 5,... n. Кроме того, сумма коэффициентов при частотах в (4.11) должна быть равной порядку комбинационной частоты М.
Таким образом, комбинационные частоты возникают при одно- временном воздействии, на НЭ не менее двух гармонических колебаний с разными частотами.
Пример 4.5. Характеристика НЭ аппроксимирована полиномом, содержащим квадратичный и кубичный члены. Входное воздействие содержит три гармонических колебания с частотами 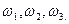 . Определить частоты всех составляющих спектра реакции.
. Определить частоты всех составляющих спектра реакции.
Поскольку в характеристику НЭ входят вторая и третья степени, в спектре реакции будет постоянная составляющая, гармоники и комбинационные часто- ты как четного, так и нечетного порядков с Мmax=З. Вычисления их проводим по соотношению (4.11).
Частоты первого порядкa: 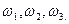 Гармоники и комбинационные частоты второго порядка: 2
Гармоники и комбинационные частоты второго порядка: 2 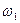 , 2
, 2 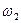 , 2
, 2 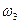 , ]
, ] 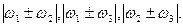
Гармоники и комбинационные частоты третьего порядка:
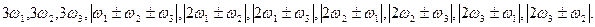
Используя принцип комбинационных частот, можно сравнительно легко подсчитать спектр реакции. Однако амплитуды гармонических составляющих спектра имеют сложный вид и относительно просто могут быть рассчитаны только при небольшом числе воздействующих частот.
Бигармоническое воздействие. Сигнал, содержащий два гармонических колебания с различными частотами 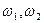 , амплитудами Xm1 и Xm2 в радиотехнике принято называть бигармоническим. Реакция НЭ с полиномиальной аппроксимацией вида (4.7) на бигармоническое воздействие содержит комбинационные частоты с амплитудами, которые определяют, применяя тригонометрические формулы кратных аргументов и произведение косинусов. Результаты вычислений при аппроксимации ВАХ полиномом третьей степени для удобства пользования приведены в спектральной табл. 4.2. Значение постоянной составляющей и амплитуд различных частот определяется как сумма элементов соответствующих строк таблицы.
, амплитудами Xm1 и Xm2 в радиотехнике принято называть бигармоническим. Реакция НЭ с полиномиальной аппроксимацией вида (4.7) на бигармоническое воздействие содержит комбинационные частоты с амплитудами, которые определяют, применяя тригонометрические формулы кратных аргументов и произведение косинусов. Результаты вычислений при аппроксимации ВАХ полиномом третьей степени для удобства пользования приведены в спектральной табл. 4.2. Значение постоянной составляющей и амплитуд различных частот определяется как сумма элементов соответствующих строк таблицы.
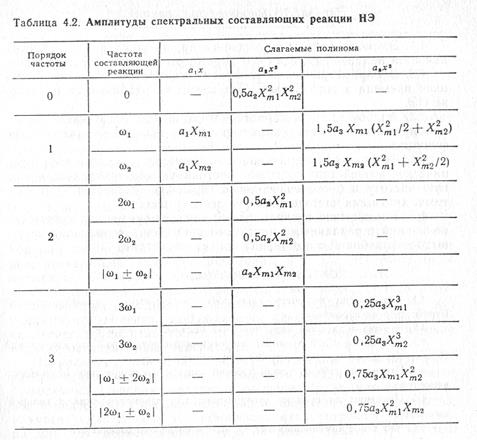
По формулам табл. 4.2 можно определить и реакцию нелинейной цепи с полиномиальной аппроксимацией на гармоническое воздействие. Для этого необходимо амплитуду сигнала с частотой 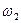 положить равной нулю.
положить равной нулю.
С помощью аналогичных выкладок можно найти и реакцию безынерционного линейно-параметрического элемента на полигармоническое воздействие. Следует отметить, что получаем при этом спектральный состав реакции значительно проще, поскольку отсутствуют гармоники частот воздействия и комбинационные частоты около них. В связи с этим линейно-параметрические элементы и цепи широко используются для получения модулированных сигналов в преобразователях частоты и т д.
Нелинейно-параметрическая цепь не подчиняется принципу суперпозиции и реакцию ее на полигармоническое воздействие необходимо определять так же, как и для нелинейной цепи. Но в спектр реакции добавляются комбинационные частоты между частотой управляющего сигнала и частотами воздействия.
Запомните основные положения
4.1. Элемент (резистор, конденсатор, катушка индуктивности) является нелинейным, если его параметры зависят от воздействия.
4.2. В параметрических элементах.параметры являются функцией времени и воздействия. Эти элементы реализуются на основе НЭ.
4.3. Аппроксимация характеристики нелинейного элемента приближенная замена характеристики простой аналитической функцией.
4.4. Реакция безынерционного нелинейного элемента на гармоническое воздействие содержит постоянную составляющую, основную частоту и бесконечное число гармоник — колебаний с частотами, кратными частоте входного воздействия.
4.5. Воздействие на нелинейный элемент суммы гармонических колебаний с различными частотами приводит к возникновению на выходе колебаний с комбинационными частотами.
КОНТРОЛЬНЫЕ ВОПРОСЫ
4.1. Какие цепи являются линейными, нелинейными, параметрическими?
Перечислите их параметры.
4.2. Что такое внешняя характеристика нелинейного элемента?
4.3. Для каких целей проводят аппроксимацию нелинейной характеристики?
Перечислите известные Вам способы аппроксимации.
4.4. Что такое рабочая точка, рабочий участок характеристики нелинейного
элемента?
4.5. Применим ли принцип суперпозиции для параметрических и нелиней-
ных цепей?
4.6. Что такое комбинационные частоты и когда они возникают?
ЗАДАЧИ
4.1. Нелинейный безынерционный элемент имеет ВАХ i (и) = a1u+a4u4
К нему приложено бигармоническое колебание. Определить число L различных
частот реакции, включая 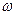 =0.
=0.
О т в е т: L = 15.
4.2. К нелинейному резистору с ВАХ i(и) = 30и + 4и2, мА, приложено напряжение 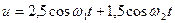 , В. Определить амплитуду тока с суммарной
, В. Определить амплитуду тока с суммарной
частотой 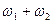
О т в е т: 15 мА.
4.3. Гармоническое напряжение с Um=5,0 В приложено к диоду, характеристику которого можно описать кусочно-линейной кривой с S=120 мА/В,
Uн=0,8 В. Найти постоянную составляющую тока через диод.
L Ответ: 141 мА.
Г л а в а 6. ПРЕОБРАЗОВАНИЕ СИГНАЛОВ
И СПЕКТРОВ В НЕЛИНЕЙНЫХ
И ПАРАМЕТРИЧЕСКИХ ЦЕПЯХ
6.1. ОБЩИЕ ПОЛОЖЕНИЯ
В системах связи некоторые полезные преобразования сигнала в процессе передачи по каналам связи сопровождаются изменением спектрального состава этого сигнала. К таким преобразованиям сигнала относятся выпрямление, резонансное усиление, умножение, деление и преобразование частоты, модуляция, детектирование и др. Большинство из них осуществляется на передающей стороне системы связи. Детектирование же (см. подробнее гл. 14) производится на приемной стороне, где помимо полезного сигнала
присутствуют помехи.
В общем случае преобразование сигнала возможно в цепи, содержащей нелинейный или параметрический элемент и частотно-избирательную нагрузку в виде фильтра, выделяющего необходимую частоту или полосу частот. Такая схема преобразования рассматривается в дальнейшем.
6.2. УМНОЖЕНИЕ ЧАСТОТЫ
Умножение частоты — это процесс увеличения частоты гармонического колебания в целое число раз. Необходимость в умножении частоты возникает в тех случаях, когда формирование колебаний на требуемой частоте по каким-либо причинам неудобно. Например, высокостабильные кварцевые генераторы устойчиво работают на частотах до 30 МГц. Умножая частоту, можно получить кварцевую стабилизацию и на более высоких частотах. В радиопередающих устройствах удвоители и утроители частоты
являются основными каскадами. Помимо снижения частоты задающего генератора такое построение схемы передатчика заметно снижает обратную реакцию более мощных каскадов на маломощные предыдущие. Умножители частоты с большой кратностью
находят также широкое применение в фазометрических устройствах, эталонах частоты, гетеродинах сантиметрового диапазона и др.
Принцип работы умножителя достаточно простой и поясняется схемой, изображенной на рис. 6.1. В цепи воздействует гармоническое колебание uвх(t) =Umcos 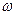 t. Форма тока i(t), в силу нелинейности диода, значительно отличается от гармонической.
t. Форма тока i(t), в силу нелинейности диода, значительно отличается от гармонической.
А это означает, что в спектре такого тока содержа ся гармоники с частотами, кратными основной частоте п-я. Полезной составляющей тока при умножении является п -я гармоника, на которую и настраивается выходной LC -контур. Для этой частоты контур
имеет достаточно большое входное резонансное сопротивление Zвх0, для других частот, в том числе и основной 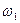 , сопротивление контура можно считать равным нулю, поэтому резонансный контур и выделяет требуемую гармонику. Изменяя частоту настройки контура, можно получить различную кратность умножения частоты. Помимо резонансного LC -контура, в умножителях применяются и другие избирательные цепи. Например, в диапазоне сантиметровых волн используются объемные резонаторы с
, сопротивление контура можно считать равным нулю, поэтому резонансный контур и выделяет требуемую гармонику. Изменяя частоту настройки контура, можно получить различную кратность умножения частоты. Помимо резонансного LC -контура, в умножителях применяются и другие избирательные цепи. Например, в диапазоне сантиметровых волн используются объемные резонаторы с
высокой добротностью (см. $ 10.3).
Амплитуда выходного напряжения умножителя частоты зависит от ВАХ нелинейного элемента и рабочей точки на этой характеристике
Umвх=InmZвх0 (6.1)
где I — амплитуда тока п -й гармоники в цепи. Расчетные фор-
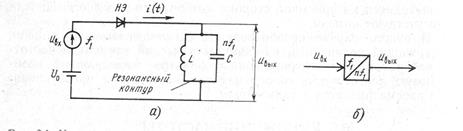
Рис. 6.1. Умножитель частоты: а – обобщенная схема; б – условное обозначение на функциональной схеме.
мулы для амплитуды тока гармоник определяются способом аппроксимации ВАХ. Например, при кусочно-линейной аппроксимации, согласно выражениям (4.9) и (6.1)
Uтвых =imax 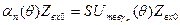
 (6.2)
(6.2)
где 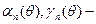 коэффициенты Берга;
коэффициенты Берга; 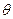 — угол отсечки; S—крутизна характеристики НЭ; Zвх0 — входное резонансное сопротивление контура. Угол отсечки, при котором п -я гармоника имеет максимальную амплитуду, равен
— угол отсечки; S—крутизна характеристики НЭ; Zвх0 — входное резонансное сопротивление контура. Угол отсечки, при котором п -я гармоника имеет максимальную амплитуду, равен 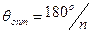 . Установка угла отсечки производится смещением Uo. Однако получить большой коэффициент умножения одной схемой с нелинейным элементом нельзя по двум причинам: 1) токи гармоник резко уменьшаются при увеличении их кратности, некоторые из гармоник могут вообще отсутствовать в зависимости от вида ВАХ; 2) трудно фильтровать незначительно отличающиеся соседние гармоники (п — 1)-ю и (п +1)-ю, наличие которых
. Установка угла отсечки производится смещением Uo. Однако получить большой коэффициент умножения одной схемой с нелинейным элементом нельзя по двум причинам: 1) токи гармоник резко уменьшаются при увеличении их кратности, некоторые из гармоник могут вообще отсутствовать в зависимости от вида ВАХ; 2) трудно фильтровать незначительно отличающиеся соседние гармоники (п — 1)-ю и (п +1)-ю, наличие которых
при плохой фильтрации приводит к паразитной амплитудной модуляции. Практически в основном реализуются схемы удвоения и утроения частоты. Для получения большого коэффициента умножения (n =103... 105) применяют многокаскадные схемы, каждая из которых имеет небольшой коэффициент умножения ni =3...5. Общий коэффициент умножения определяется как произведение коэффициентов умножения всех каскадов: п = п1 п2... nk.
Пример 6.1. В утроителе частоты (см. рис. 6.1, a) применен НЭ, ВАХ которого при u>Uн можно аппроксимировать прямой с S=0,2 мА/В. Добротность контура Q=80. Определить амплитуду выходного напряжения, если на вход подано напряжение амплитудой Um вх=0,2 В и частотой f1 =20 МГц.
Выбираем емкость контура по рекомендациям, приведенным в примере 5.1
(2 пФ на метр длины волны). Для частоты 3f1 = 60 МГц (длинна волны 5 м),
С =10 пФ. Характеристическое сопротивление контура 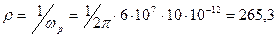 Ом, откуда входное резонансное сопротивление Zвх0=
Ом, откуда входное резонансное сопротивление Zвх0= 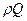 =21,22 кОм.
=21,22 кОм.
Для утроителя частоты оптимальный угол отсечки 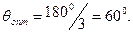 Из
Из
графиков рис. 4.8 находим 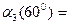 0,13 и, согласно (4.10),
0,13 и, согласно (4.10), 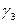 (600) =
(600) =
(1 — соs 600).0,13=6,5 *10-2
По (6.2) амплитуда напряжения на выходе утроителя частоты 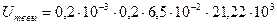 =0,055 В.
=0,055 В.
Принцип преобразования частоты. Преобразованием частоты называется перенос спектра модулированного сигнала из окрестности несущей частоты 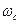 , в окрестность некоторой промежуточной частоты
, в окрестность некоторой промежуточной частоты 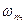 . При преобразовании частоты сохраняются амплитудные и фазовые соотношения между составляющими спектра сигнала, изменяются только частоты составляющих, т. е. перенос спектра совершается без изменения закона модуляции.
. При преобразовании частоты сохраняются амплитудные и фазовые соотношения между составляющими спектра сигнала, изменяются только частоты составляющих, т. е. перенос спектра совершается без изменения закона модуляции.
Как известно (см. $ 4.5), при подаче на нелинейный элемент колебаний с двумя разными частотами 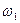 и
и 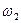 на выходе можно получить комбинационные составляющие в виде суммы
на выходе можно получить комбинационные составляющие в виде суммы 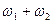 или разности
или разности 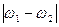 частот. Если избирательной цепью выделить одну из них, например разностную, то это и будет колебание промежуточной частоты
частот. Если избирательной цепью выделить одну из них, например разностную, то это и будет колебание промежуточной частоты 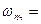
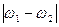 . Таким образом, если
. Таким образом, если 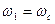 то для получения промежуточной частоты требуется напряжение от вспомогательного генератора
то для получения промежуточной частоты требуется напряжение от вспомогательного генератора 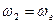 который называют гетеродином. В качестве нелинейного элемента обычно применяется безынерционный параметрический элемент — смеситель.
который называют гетеродином. В качестве нелинейного элемента обычно применяется безынерционный параметрический элемент — смеситель.
Как смеситель используются различные электронные приборы, в которых сигнальное и гетеродинное напряжения подаются на один и тот же или различные электроды: биполярные транзисторы, одно- или многосеточные лампы, полевые транзисторы с одним или двумя затворами, дифференциальные усилители, кристаллические диоды (в СВЧ диапазоне) и др.
Под действием периодического напряжения гетеродина и,(t) дифференциальная крутизна Sдиф ВАХ смесителя периодически меняется. А периодическую функцию Sдиф (t) можно разложить в ряд Фурье
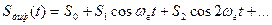 , (6.3)
, (6.3)
где S0, Si, S2 — коэффициенты разложения. Для практических расчетов можно ограничиться двумя членами в этом разложении. При подаче на вход преобразователя (рис. 6.2) модулированного сигнала, например АМ, uc(t) = 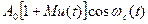 переменная составляющая выходного тока согласно (6.3)
переменная составляющая выходного тока согласно (6.3)
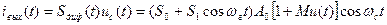
Это выражение можно представить в виде
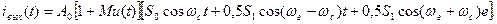 (6.4)
(6.4)
Выходное напряжение преобразователя ивых пропорционально слагаемому разностной частоты 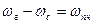 в (6.4), так как на эту частоту настроен колебательный контур в коллекторной цепи транзисторного смесителя
в (6.4), так как на эту частоту настроен колебательный контур в коллекторной цепи транзисторного смесителя
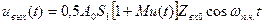 (6.5)
(6.5)
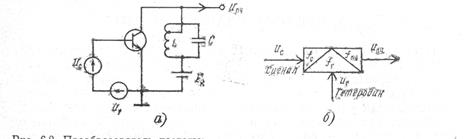
Рис. 6.2. Преобразователь частоты: а – обобщенная схема; б – условное обозначение на функциональной схеме
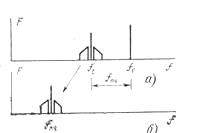
Рис. 6.3. Перенос спектров в преобразователе частоты: а – спектра на входе смесителя; б – спектр на выходе смесителя.
Из выражения (6.5) следует, что и вых(t) является АМ колебанием с тем же законом модуляции, что и входной сигнал, произошло только смещение частоты несущей. Это преобразование показано на рис. 6.3, где изображены спектры входного и выходного сигналов преобразователя. Перенос спектра входного сигнала означает, что колебательный контур преобразователя должен иметь полосу пропускания, достаточную для неискаженного выделения спектра модулированного сигнала.
Крутизна преобразования. Эффективность работы преобразователя принято характеризовать особым параметром— крутизной преобразования, равной отношению амплитуды тока промежуточной частоты на выходе преобразователя к амплитуде немодулированного напряжения сигнала, приложенного к входу:
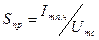
Для вычисления Sпр необходимо знать зависимость дифференциальной крутизны Sдиф(и), определить закон изменения во времени Sдиф (t) под воздействием напряжения гетеродина и далее вычислить амплитуду первой гармоники разложения Sдиф в ряд Фурье. Это довольно сложная процедура. В практических расчетах можно считать, что под воздействием напряжение гетеродина Sдиф изменяется от 0 до Smax Тогда крутизна преобразования 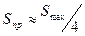 при гармоническом изменении
при гармоническом изменении 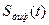 и
и 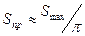 при прямоугольном изменении Sдиф(t). Следовательно, в любом режиме преобразования крутизна преобразования имеет порядок
при прямоугольном изменении Sдиф(t). Следовательно, в любом режиме преобразования крутизна преобразования имеет порядок
 (6.6)
(6.6)
которым и пользуются в практических расчетах. При этом следует учитывать, что максимальная крутизна пропорциональна амплитуде гетеродина. Отношение амплитуды выходного напряжения сигнала на промежуточной частоте к амплитуде воздействующего сигнала называется коэффициентом передачи (усиления) преобразователя Кпр. Как и для любого резонансного усилителя коэффициент усиления преобразователя Kпр=Sпр Zвх0, где Zвх0 — входное резонансное сопротивление контура. Из (6.6) следует, что коэффициент усиления любого каскада в режиме преобразования частоты примерно в 3... 4 раза меньше, чем в режиме усиления.
Расчет преобразователя частоты обычно сводится к определению частоты и амплитуды гетеродина, избирательного контура, коэффициента передачи или выходного напряжения сигнала при заданных входном сигнале и параметрах нелинейного элемента. Ниже приводится пример такого расчета.
Принцип получения дробного коэффициента деления р/п достаточно прост: сначала частота делится п раз, а далее — умножается р раз. Осуществление вышеописанной операции в другом порядке — сначала умножение, а далее деление — нежелательно
из-за усложнения схем умножителей и делителей на более высоких частотах.
6.5. ХАРАКТЕРИСТИКИ МОДУЛЯТОРОВ
Модуляция несущего колебания осуществляется с помощью
специальных устройств — модуляторов, построение которых определяется видом модуляции. С помощью модуляторов физически реализуются операции, характерные для различных видов модуляции (см. гл. 3). Качественные показатели модуляторов принято оценивать по модуляционной характеристике, под которой понимают зависимость отклонения информационного параметра несущей от воздействующего постоянного модулирующего напряжения U м. При гармонической несущей в модуляционной характеристике по оси ординат откладывается отклонение: амплитуды 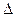 А при АМ, частоты
А при АМ, частоты 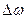 при ЧМ, фазы
при ЧМ, фазы 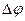 при ФМ (рис. 6;5).Обычно эта характеристика снимается экспериментально для конкретной схемы модулятора. Как для АМ, так и для ЧМ и ФМ
при ФМ (рис. 6;5).Обычно эта характеристика снимается экспериментально для конкретной схемы модулятора. Как для АМ, так и для ЧМ и ФМ
модуляционная характеристика в идеальном случае должна быть линейной. Отклонение от линейной зависимости свидетельствует о нелинейных искажениях. Именно по допустимой величине нелинейных искажений выбирают амплитуду модулирующего сиг-
нала для конкретной схемы модулятора.
Частотные свойства модуляторов определяются по частотной характеристике, под которой понимают зависимость основного параметра модулированного сигнала от частоты модулирующего гармонического сигнала им (t) (при постоянной амплитуде). Для
гармонической несущей такими основными параметрами являются — коэффициент модуляции М при АМ, девиация частоты 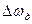 , при ЧМ и девиация фазы
, при ЧМ и девиация фазы 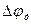 при ФМ. Частотная характеристика в идеальном случае имеет вид прямой, параллельной оси
при ФМ. Частотная характеристика в идеальном случае имеет вид прямой, параллельной оси
частот (рис. 6.6). Отклонение от прямой позволяет определить
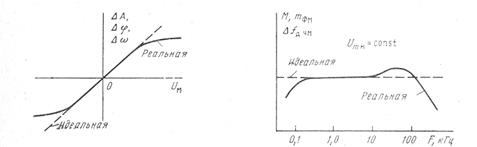
Рис. 6.5. Модуляционная Рис. 6.6. Частотная характеристика
 2015-05-26
2015-05-26 6532
6532
