2015-05-26
908
Немецкий физик Г.Ом экспериментально установил закон, согласно которому: сила тока, текущего по однородному проводнику, пропорциональна разности потенциалов на его концах (напряжению U)
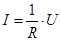, где R-электрическое сопротивление проводника.
Сопротивление R зависит от формы и размеров проводника, от его материала и температуры проводника.
В простейшем случае однородного цилиндрического проводника
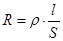, где (1)
l - длина проводника
S- площадь его поперечного сечения
ρ-удельное электрическое сопротивление (зависит от материала и температуры проводника) [ρ]=Ом·м
Для большинства металлов R и ρ зависят от температуры следующим образом:
,
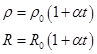где α-термический коэффициент сопротивления.
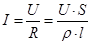
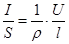
Учитывая (1) закон Ома можно записать закон Ома в ви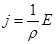де:
, где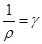 
- удельная электрическая проводимость вещества проводника
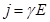
Так как в изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора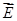 
, то направление векторов 
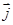и 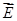совпадают, следовательно
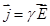- закон Ома в дифференциальной форме (2)
|
|
|
Таким образом, мы получили связь между векторам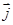и и 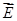в одной и той же точке проводника.
Получим закон Ома для неоднородного участка цепи.
На неоднородном участке цепи на носители тока кроме электростатических сил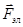 
, действуют сторонние силы 
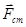. Тогда, если под действием электрического поля Е в проводнике возникает ток плотности 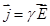,то очевидно, что под совместным действием поля 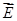и поля сторонних сил 
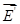плотность тока
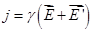(3)
Это уравнение обобщает закон (2) на случай неоднородного проводника. Оно выражает закон Ома для неоднородного проводника в дифференциальной форме.
Перейдём к интегральной форме закона Ома для неоднородного участка цепи.
Домножим обе части уравнения (3) на вектор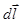 
, численно равный длине сегмента проводника и направленный вдоль проводника в направлении тока:
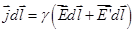или, учитывая, что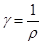 
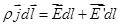
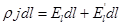
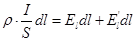
Интегрируем полученное выражение по длине участка цепи
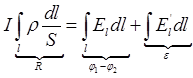
IR=φ1-φ2+ε=U -закон Ома для неоднородного участка цепи
