Закон Джоуля-Ленца

Рассмотрим однородный проводник на концах которого создана разность потенциалов 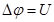. За время dt по проводнику проходит заряд d q

d q = I ·d t

При этом электрическое поле совершает работу, называемую работой тока dA_I

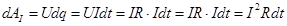
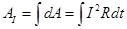
Согласно закону сохранения энергии эквивалентная этой работе энергия должна выделяться в иной форме. Если проводник неподвижен и в нём не происходят химические превращения, то эта энергия должна выделяться в форме внутренней (тепловой) энергии, в результате чего проводник нагревается

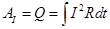
Эта формула выражает установленный экспериментально Джоулем и независимо от него Ленцем закон, называемый законом Джоуля-Ленца.

Получим закон Джоуля-Ленца в локальной (дифференциальной) форме, характеризующей выделение теплоты в различных местах проводника.

Выделим в проводящей среде элементарный объём в виде цилиндрика с образующими параллельными вектору 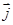-плотности тока в данном месте. Пусть поперечное сечение цилиндрика dS, а его длина dl. Тогда на основании закона Джоуля-Ленца в этом объёме за время dt выделяется количество теплоты

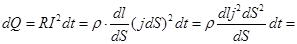/ dldS=dV /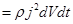

Разделив на dVdt получаем

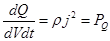-удельная тепловая мощность тока

Закон Джоуля-Ленца в дифференциальной форме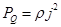

Удельная тепловая мощность тока пропорциональна квадрату плотности тока и удельному сопротивлению среды в данной точке.