Уравнение непрерывности

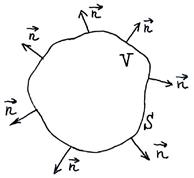
Рассмотрим воображаемую замкнутую поверхность S в некоторой проводящей среде, по которой течет электрический ток. Для замкнутых поверхностей вектор нормали 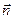и вектор 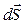принято брать направленными наружу:

Поэтому 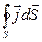– заряд, выходящий в единицу времени наружу из объема V, охватываемого замкнутой поверхностью S.

На основании закона сохранения заряда 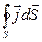равен убыли заряда в единицу времени внутри объема V: 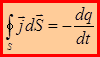– уравнение непрерывности в интегральной форме.

Используя, что 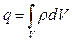имеем: 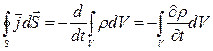(здесь V и t независимые переменные, поэтому производная по времени может быть внесена в интеграл по объему, полную производную по времени следует заменить на частную производную по времени поскольку 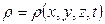, вместе с тем 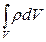является функцией только времени.

Согласно теореме Остроградского–Гаусса: 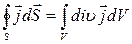. Отсюда: 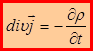– уравнение непрерывности в дифференциальной форме.

Или: 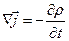, где 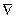– оператор Гамильтона или набла-оператор; в декартовой системе координат 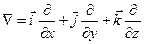и с учетом сказанного уравнение непрерывности в декартовой системе координат имеет вид: .

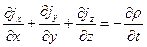Согласно уравнению непрерывности в точках, которые являются источником 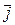происходит убывание объемной плотности заряда, в точках, которые являются стоком вектора 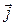происходит увеличение объемной плотности заряда. Для постоянных токов 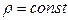, поэтому в цепи постоянного тока для всех точек 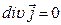. Следовательно, поток вектора 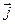через любую замкнутую поверхность равен нулю, а значит – для постоянных токов линии тока непрерывны.