Рассмотрим случай, когда электрический ток течет вдоль тонких проводов. В этом случае направление тока будет совпадать с направлением оси провода и модуль плотности тока j может считаться одинаковым во всех точках сечения провода. Пусть площадь сечения провода равна S.
 Разделим левую и правую часть уравнения, выражающее обобщенный закон Ома (
Разделим левую и правую часть уравнения, выражающее обобщенный закон Ома (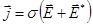 ), на удельную электрическую проводимость проводника
), на удельную электрическую проводимость проводника 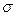 , полученное уравнение умножим скалярно на элемент провода
, полученное уравнение умножим скалярно на элемент провода 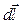 , взятый по направлению от сечения 1 к сечению 2 (это направление примем за положительное), а затем проинтегрируем по длине провода от 1 до2:
, взятый по направлению от сечения 1 к сечению 2 (это направление примем за положительное), а затем проинтегрируем по длине провода от 1 до2: 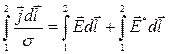 .
.
Преобразуем подынтегральное выражение у первого интеграла: заменим 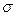 на
на 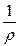 , и
, и 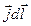 на
на 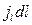 , где
, где 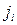 – проекция вектора плотности тока
– проекция вектора плотности тока 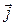 на направление вектора
на направление вектора 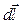 . Далее учтем, что
. Далее учтем, что 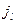 – величина алгебраическая: если
– величина алгебраическая: если 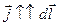 , то
, то 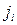 > 0; если же
> 0; если же 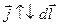 , то
, то 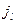 < 0. Затем заменим
< 0. Затем заменим 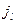 на
на 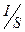 , где I – сила тока, величина также алгебраическая (как и
, где I – сила тока, величина также алгебраическая (как и 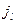 ). Для постоянного тока величина I можно вынести за знак интеграла. В результате
). Для постоянного тока величина I можно вынести за знак интеграла. В результате
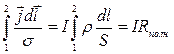 ,
,
где 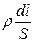 – сопротивление участка цепи длиной dl, а
– сопротивление участка цепи длиной dl, а 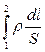 – полное сопротивление (Rполн.) участка цепи между сечениями 1 и 2:
– полное сопротивление (Rполн.) участка цепи между сечениями 1 и 2: 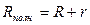 , где R – внешнее сопротивление, r – внутреннее сопротивление источника тока.
, где R – внешнее сопротивление, r – внутреннее сопротивление источника тока.
В правой части рассматриваемого уравнения 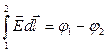 – разность потенциалов, а
– разность потенциалов, а 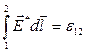 – электродвижущая сила, действующая на рассматриваемом участке цепи.
– электродвижущая сила, действующая на рассматриваемом участке цепи.
 Величина
Величина 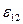 является алгебраической: если э.д.с. способствует движению положительных носителей тока в выбранном направлении, то
является алгебраической: если э.д.с. способствует движению положительных носителей тока в выбранном направлении, то 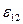 >0, если же препятствует, то
>0, если же препятствует, то 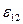 <0.
<0.
Итоговое выражение имеет вид:  – интегральная форма закона Ома для неоднородного участка цепи. Отсюда можно получить соотношения для частных случаев:
– интегральная форма закона Ома для неоднородного участка цепи. Отсюда можно получить соотношения для частных случаев:
- закон Ома для замкнутой цепи (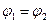 ):
): 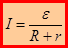 , где
, где 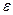 – алгебраическая сумма отдельных э.д.с. в замкнутой цепи;
– алгебраическая сумма отдельных э.д.с. в замкнутой цепи;
- если источник разомкнут, то 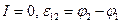 , т.е. э.д.с. источника определяется как разность потенциалов на клеммах источника в разомкнутом состоянии.
, т.е. э.д.с. источника определяется как разность потенциалов на клеммах источника в разомкнутом состоянии.
 2015-05-26
2015-05-26 2389
2389








