Закон Ома.
Средний путь, проходимый свободно движущимися электронами между двумя последовательными столкновениями с ионами решетки называется средней длинной свободного пробега 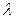 . Среднее время между двумя столкновениями
. Среднее время между двумя столкновениями 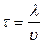 (определяется скоростью хаотического движения). При наличии поля
(определяется скоростью хаотического движения). При наличии поля  направленная скорость электронов накапливается за время свободного пробега и к моменту следующего соударения достигает максимальной величины:
направленная скорость электронов накапливается за время свободного пробега и к моменту следующего соударения достигает максимальной величины:
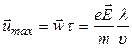 .
.
Скорость 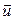 изменяется за время пробега линейно. Поэтому ее среднее за пробег значение равно половине максимального значения.
изменяется за время пробега линейно. Поэтому ее среднее за пробег значение равно половине максимального значения.
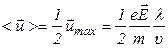
Плотность тока:
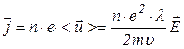
Коэффициент пропорциональности между 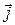 и
и  обозначим
обозначим 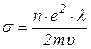 (
(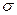 - проводимость). В результате получим закон Ома в локальной форме (параметры относятся к данной точке сечения проводника).
- проводимость). В результате получим закон Ома в локальной форме (параметры относятся к данной точке сечения проводника).
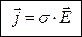
Плотность тока в проводнике пропорциональна напряженности электрического поля  . Коэффициентом пропорциональности является проводимость. (Замечание. Сравним полученную формулу с известной
. Коэффициентом пропорциональности является проводимость. (Замечание. Сравним полученную формулу с известной 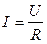 . Проводимость
. Проводимость 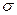 обратно пропорциональна удельному сопротивлению
обратно пропорциональна удельному сопротивлению 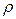
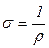 . Плотность тока
. Плотность тока 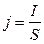 . Напряженность поля
. Напряженность поля 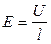 (
(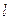 - длинна проводника). Тогда
- длинна проводника). Тогда 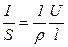 , или
, или 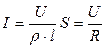 , что и требовалось.)
, что и требовалось.)
Закон Джоуля – Ленца.
К концу свободного пробега электрон приобретает дополнительную кинетическую энергию, среднее значение которой равно:
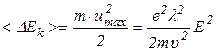
(Напомним: 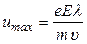 ).
).
Столкнувшись с атомом, электрон, по предположению, полностью передает приобретенную им энергию кристаллической решетке. Сообщенная решетке энергия идет на увеличение внутренней энергии металла, проявляясь в его нагревании.
Каждый электрон претерпевает за секунду в среднем 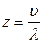 соударений. Обозначим число электронов проводимости в единице объема
соударений. Обозначим число электронов проводимости в единице объема 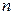 , тогда полная энергия, переданная электронами за единицу времени в единице объема будет равняться:
, тогда полная энергия, переданная электронами за единицу времени в единице объема будет равняться:
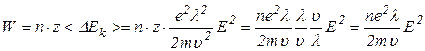 .
.
Зная, что 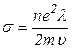 в результате получим закон Джоуля – Ленца в локальной форме:
в результате получим закон Джоуля – Ленца в локальной форме:
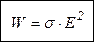
Тепловая мощность, выделяющаяся в единице объема при протекании электрического тока пропорциональна квадрату напряженности поля.
Переходя от 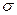 и
и 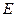 к
к 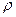 и
и 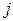 : (
: (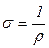 ,
, 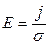 ), получим
), получим 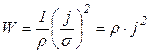 , или
, или
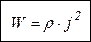
Получили другую форму закона Джоуля – Ленца. (Объемная плотность тепловой мощности равна произведению удельного сопротивления на квадрат плотности тока).
 2015-05-26
2015-05-26 2510
2510








