Совокупность векторов электрических величин, изображённых в общей координатной системе, называется векторной диаграммой

Используя закон Ома, записываем, что

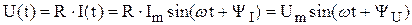где 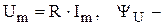фаза напряжения, .

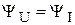Полученный результат говорит о том, что амплитуда напряжения пропорциональна амплитуде тока, начальные фазы равны между собой и фазовый сдвиг (это разность фаз!) между током и напряжением равен нулю.

На рисунках вверху (средний) показана соответствующая векторная диаграмма и временная развёртка тока и напряжения на резисторе (справа).

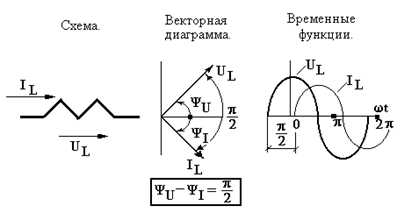
б) Идеальный индуктивный элемент L.

Дано:

По участку цепи с индуктивным элементом 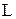проходит ток 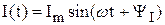, где 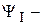начальная фаза тока.

Найти:

Напряжение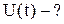

Решение.

При протекании тока, в цепи возбуждается э.д.с. самоиндукции .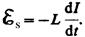

Согласно второму правилу Кирхгофа с учётом знаков, можно записать, что

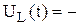ε_S ,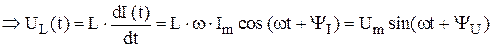

где 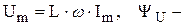фаза напряжения, .

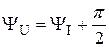По аналогии с законом Ома для резистора в данном случае можно ввести понятие индуктивного сопротивления.

Определение 2.

Коэффициент пропорциональности между амплитудами напряжения и тока, а именно 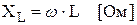, называется индуктивным сопротивлением индуктивного элемента.

Тогда .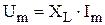

Полученные результаты говорят о том, что амплитуда напря жения пропорциональна амплитуде тока (с коэффициентом пропорциональности, равным индуктивному сопротивлению), а фазовый сдвиг между током и напряжением равен 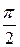(напряжение опережает ток на четверть периода!), в отличие от резистивного элемента, где таковой отсутствовал!

На рисунках вверху (средний) показана соответствующая векторная диаграмма и временная развёртка тока и напряжения на индуктивном элементе (справа).

б) Идеальный ёмкостной элемент С.

Дано:

По участку цепи с емкостным элементом 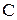проходит ток 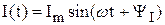, где 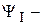начальная фаза тока..

Найти: Напряжение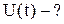

Решение.

Если в цепи протекает ток, то заряд на ёмкости будет равен .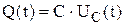

По определению 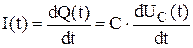или .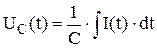

Подставляя под знак интеграла выражение для тока (постоянную интегрирования принимакем равной нулю, так как, физически, постоянная составляющая напряжения на ёмкости отсутствует!), находим, что

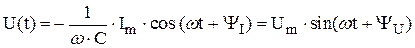где .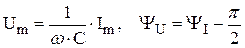

По аналогии с законом Ома для резистора в данном случае можно ввести понятие ёмкостного сопротивления.

Определение 3.

Коэффициент пропорциональности между амплитудами напряжения и тока, а именно 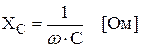, называется екостным сопротивлением емкостного элемента.

Тогда .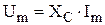

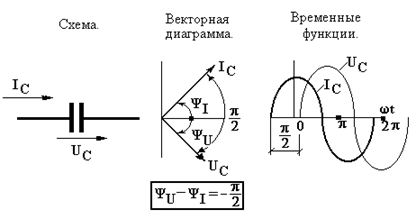
Полученные результаты говорят о том, что амплитуда напряжения пропорциональна амплитуде тока (с коэффициентом пропорциональности, равным емкостному сопротивлению), а фазовый сдвиг между током и напряжением равен 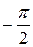(ток опережает напряжение по фазе на четверть периода!), в отличие от резистивного элемента, где таковой отсутствовал!