Рассмотрим схему из последовательно соеди напряжений нённых идеализированных элементов  , отличительной особенностью которой являетсявозможность явления,называемого резонансом напряжений.
, отличительной особенностью которой являетсявозможность явления,называемого резонансом напряжений.
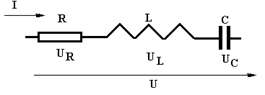 Пусть в цепи протекает синусоидальный ток –
Пусть в цепи протекает синусоидальный ток – 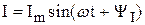 .
.
Расчётные соотношения для токов и напряжений на элементах рассматриваемого участка цепи были получены ранее.
Аналогичным образом, можно получить соотношение, связывающее ток и напряжение для всего участка в целом.
Опуская промежуточные выкладки, записываем, что суммарное падение напряжения будет равно
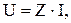
где 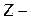 так называемое, полное сопротивление участка последовательно соединённых идеализированных элементов –
так называемое, полное сопротивление участка последовательно соединённых идеализированных элементов – 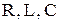 , которое определяет пропорциональную связь между модулями напряжения и тока –
, которое определяет пропорциональную связь между модулями напряжения и тока – 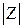 , а также сдвиг по фазе между ними –
, а также сдвиг по фазе между ними – 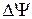 .
.
Итак,
· модуль полного сопротивления – 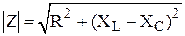 ;
;
· фазовый сдвиг напряжения относительно тока – 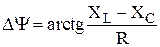 .
.
Примечание. Величина суммарного фазового сдвига определяется активным и реактивными сопротивлениями. В зависимости от их величин 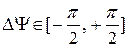 .
.
Особенностью рассмотренной схемы, как указано ранее, является возможность возникновения, так называемого, «резонанса напряжений».
Физически, это явление предполагает равенство амплитуд напряжений на реактивных элементах при противоположной их направленности. В этом случае падение напряжения происходит только на резисторе.
Обратимся к выражениям для модуля полного сопротивления и фазового сдвига..
При резонансе полное сопротивление цепи должно быть минимальным. Это возможно, когда  . В этом случае
. В этом случае 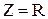 , фазовый сдвиг -
, фазовый сдвиг - 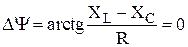 , а ток
, а ток 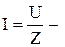 максимален.
максимален.
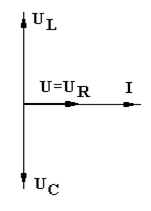 Из равенства
Из равенства  следует условие возникновения резонанса в терминах частоты сигнала, а именно,
следует условие возникновения резонанса в терминах частоты сигнала, а именно,
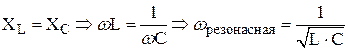 .
.
Специфическая векторная диаграмма, соответствующая рассматриваемому резонансу напряжений, показана на рисунке слева.
 2015-05-26
2015-05-26 172
172







