Лабораторная работа 6
Конденсатор в цепи переменного тока
Цель работы. Исследование зависимости проводимости конденсатора от частоты синусоидального тока. Определение емкости конденсатора и диэлектрической проницаемости вещества, заполняющего конденсатор.
Приборы и оборудование. Плоский конденсатор, диэлектрическая пластина, генератор синусоидального напряжения, два цифровых вольтметра.
Теоретическая часть
В работе исследуется плоский конденсатор, который представляет собой две плоские проводящие пластины (обкладки), расположенные параллельно друг другу, причем заряд одной пластины q, а другой пластины (- q). Расстояние между пластинами d предполагается малым по сравнению с линейными размерами пластин. В этом случае электрическое поле 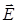 между пластинами можно считать однородным (рис.1), а распределение зарядов по пластинам равномерным:
между пластинами можно считать однородным (рис.1), а распределение зарядов по пластинам равномерным:
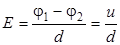 ,
, 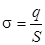 , (1)
, (1)
где 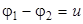 - разность потенциалов между пластинами – напряжение на конденсаторе,
- разность потенциалов между пластинами – напряжение на конденсаторе, 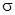 - поверхностная плотность заряда, S - площадь пластины.
- поверхностная плотность заряда, S - площадь пластины.
Для напряженности электрического поля в конденсаторе при помощи теоремы Гаусса можно найти
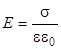 , (2)
, (2)
где 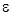 - диэлектрическая проницаемость вещества между пластинами,
- диэлектрическая проницаемость вещества между пластинами, 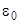 - электрическая постоянная, и тогда из формул (1), (2) следует, что заряд конденсатора пропорционален приложенному к нему напряжению
- электрическая постоянная, и тогда из формул (1), (2) следует, что заряд конденсатора пропорционален приложенному к нему напряжению
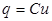 . (3)
. (3)
Коэффициент пропорциональности
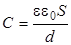 (4)
(4)
называют электроемкостью (или просто емкостью) конденсатора.
Заметим, что, строго говоря, поверхностная плотность заряда s не является постоянной по всей поверхности пластины, а увеличивается вблизи ее краев. Вблизи краев нарушается также предположение об однородности электрического поля, поэтому формулы (1), использованные при выводе (4), являются приближенными. Они выполняются тем точнее, чем меньше отношение d к линейным размерам пластин конденсатора.
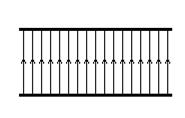 | 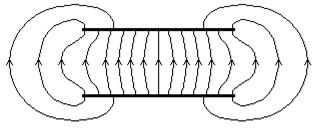 |
| Рис.1. Поле плоского конденсатора без учета краевых эффектов | Рис.2. Поле плоского конденсатора с учетом краевых эффектов |
Схематически поле плоского конденсатора с учетом отмеченных выше краевых эффектов изображено на рис. 2. Как видно из рисунка, линии поля сгущаются вблизи краев конденсатора, что связано с концентрацией заряда у краев пластин. Кроме того, некоторые линии поля начинаются и заканчиваются не на внутренних, а на внешних поверхностях пластин. Это означает, что некоторая часть заряд располагается на внешних поверхностях пластин конденсатора. Заметим, что общее число линий поля на рис.1 и рис.2 одинаково, если одинаковы заряды соответствующих пластин на рис.1 и рис. 2.
Строгий расчет емкости плоского конденсатора с учетом краевых эффектов представляет собой сложную задачу. Приведем без вывода приближенную формулу, учитывающую краевые эффекты для плоского конденсатора с круглыми пластинами:
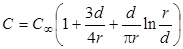 , (5)
, (5)
где 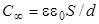 - емкость конденсатора без учета краевых эффектов, r - радиус пластины (
- емкость конденсатора без учета краевых эффектов, r - радиус пластины (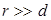 ). Второе слагаемое в (5) учитывает оттеснение заряда к краям пластин, третье слагаемое – частичное вытеснение заряда на внешние поверхности пластин.
). Второе слагаемое в (5) учитывает оттеснение заряда к краям пластин, третье слагаемое – частичное вытеснение заряда на внешние поверхности пластин.
Если в пространство между обкладками конденсатора параллельно им ввести плоскую пластину толщиной 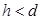 из диэлектрика с проницаемостью
из диэлектрика с проницаемостью 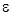 , то емкость конденсатора будет равна
, то емкость конденсатора будет равна
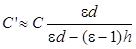 , (6)
, (6)
где C - емкость конденсатора без диэлектрика.
Отметим, что любую пару проводников, независимо от их формы и расположения, можно считать конденсатором. И в этом случае емкостью конденсатора называют коэффициент пропорциональности между зарядом конденсатора (так называют заряд положительной обкладки, заряд другой обкладки конденсатора такой же по величине, но отрицательный) и разностью потенциалов между обкладками. Емкость конденсатора зависит от геометрических размеров обкладок, их взаимного расположения и диэлектрической проницаемости среды.
Рассмотрим теперь случай, когда конденсатор включен в цепь переменного тока. Одно из направлений тока примем за положительное (оно обозначено на рис.3 стрелкой). Обозначим через 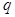 заряд той из обкладок конденсатора, направление от которой к другой обкладке совпадает с положительным направлением тока. Напряжение между точками а и b обозначим через u. Тогда
заряд той из обкладок конденсатора, направление от которой к другой обкладке совпадает с положительным направлением тока. Напряжение между точками а и b обозначим через u. Тогда
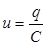 ,
, 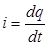
и, следовательно, 
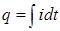 .
.
Если сила тока в цепи изменяется по закону
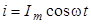 , (7)
, (7)
(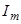 - амплитуда тока,
- амплитуда тока, 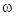 - циклическая частота), то заряд конденсатора равен
- циклическая частота), то заряд конденсатора равен
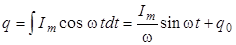 .
.
Постоянная интегрирования q 0 обозначает произвольный постоянный заряд конденсатора, не связанный с колебаниями тока, и поэтому мы положим 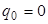 . Следовательно,
. Следовательно,
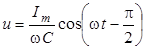 . (8)
. (8)
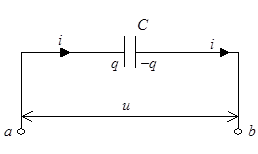 Рис.3. Конденсатор в цепи переменного тока Рис.3. Конденсатор в цепи переменного тока | 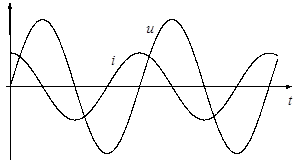 Рис.4. Зависимость тока и напряжения от времени Рис.4. Зависимость тока и напряжения от времени |
Сравнивая (7) и (8), видим, что при синусоидальных колебаниях тока в цепи колебания напряжения на конденсаторе отстают по фазе от колебаний тока на p/2. Изменения тока и напряжения во времени изображены графически на рис.4.
Формула (8) показывает, что амплитуда напряжения на конденсаторе равна
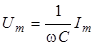 . (9)
. (9)
Сравнивая это выражение с законом Ома для участка цепи с постоянным током (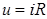 ), видим, что величина
), видим, что величина
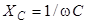
играет роль сопротивления участка цепи, она получила название емкостного сопротивления. Емкостное сопротивление зависит от частоты w, поэтому при очень высоких частотах даже малые емкости могут представлять совсем небольшое сопротивление для переменного тока. Важно отметить, что емкостное сопротивление определяет связь между амплитудными, а не мгновенными значениями тока и напряжения.
В цепях переменного тока обычно измеряют не амплитудные, а эффективные значения тока и напряжения:
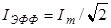 ,
, 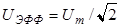 .
.
Эффективное напряжение на конденсаторе далее будем обозначать 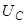 . Тогда вместо (9) запишем
. Тогда вместо (9) запишем
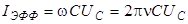 (10)
(10)
где 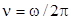 - частота. Это соотношение проверяется в работе экспериментально.
- частота. Это соотношение проверяется в работе экспериментально.
 2015-05-26
2015-05-26 1900
1900