2015-05-26
353
Лабораторная работа № 5.
Определение активной и реактивной мощности в цепях переменного тока.
Краткая теория.
Согласно закону Джоуля – Ленца мощность, выделяемая в цепи постоянного тока равна:
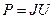, (1)
где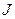 
- ток в проводнике, а 
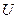- напряжение на концах проводника.
Если использовать закон Ома, то можно записать:
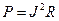(2)
или
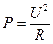. (3)
В цепях переменного тока при наличии емкости и индуктивности, между током и напряжением возникает сдвиг фаз. При последовательном соединении сопротивления, емкости и индуктивности напряжение на этих элементах не совпадает по фазе: напряжение на индуктивности отстает по фазе от напряжения на сопротивлении на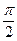 
, а напряжение на емкости напротив опережает напряжение на сопротивлении на .
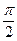Это обстоятельство позволяет построить векторную диаграмму для амплитудных значений напряжения для этих трех элементов (рис.1). Концы векторов указывают на амплитудные значения напряжений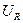 
, 
, 
.
 |
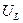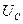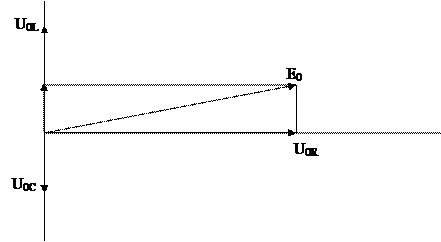Рис.1.
Напряжение на емкости и индуктивности оказываются в противофазе, то есть, сдвинуты по фазе на π. Амплитудное значение напряжения на всей цепи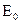 
можно просто найти векторным сложением, как показано на рис. 1.
При последовательном соединении ток в цепи один и тот же – i. Активное сопротивление обозначается R, индуктивное сопротивление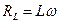 
, емкостное 
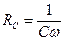, где L –индуктивность, С – емкость, 
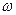- круговая частота 
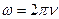. В промышленной сети 
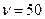Гц.
Таким образом, из векторной диаграммы непосредственно вытекает закон Ома для полной цепи переменного тока:
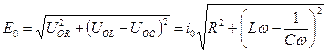, (4)
Отсюда
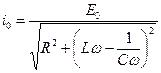. (5)
Выражение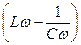 
называется импедансом цепи. Из векторной диаграммы легко можно увидеть, что сдвиг фаз между амплитудой ЭДС (E0) и амплитудными значениями тока 
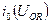равен 
:
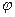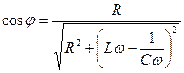. (6)
Теперь рассмотрим, какая мощность выделится в цепи переменного тока на сопротивлении R. Пусть напряжение изменяется по закону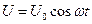 
, тогда за один период колебания будет выделяться теплота:
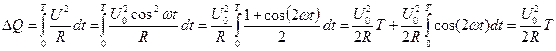, (7)
так как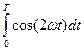 
=0, то
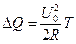. (8)
Теплота, выделяемая за единицу времени, т.е. мощность, равна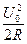 
, где U0 амплитудное значение напряжения. Это значит, что, если бы мы взяли напряжение 
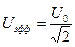, то получили бы формулу мощности как для постоянного тока: 
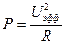или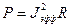 
. Таким образом, 
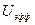называют эффективным или действующим напряжением, так как такое напряжение выделяет такое же количество тепла, как и при постоянном токе. Так как амплитудные значения тока и напряжения отличается от эффективных в 
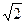раз, то закон Ома для амплитудных значений (5) может быть записан через эффективные значения, т.е.:
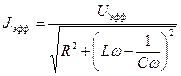. (9)
Отсюда мощность, выделяемая на сопротивлении при переменном токе в цепи:
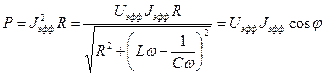, (10)
где 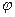- сдвиг фаз между током и напряжением во всей цепи.
В случае, когда цепь состоит только из сопротивления и емкости, выражение (6) и (9) запишутся в виде:
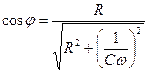, (11)
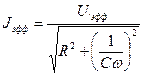, (12)
отсюда, подставив (11), (12) в (10), получим
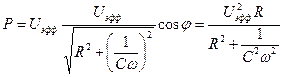. (13)
Подавая на RC – цепь постоянное по величине напряжение Uэфф и меняя активное сопротивление R можно исследовать функцию P(R).
Продифференцировав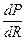 
, получим
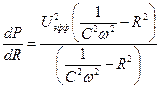. (14)
Приравняв выражение (14) к нулю, находим, что при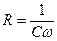 
мощность принимает максимальное значение.
Мощность, равная
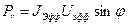(15)
называется реактивной мощностью. Она не может быть выделена в форме тепла, поэтому при производстве электроэнергии её стремятся сделать как можно меньше.
Полная мощность
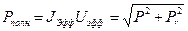. (16)
