Коэффициент мощности и его значение

Коэффициентом мощности (cosφ) электрической сети называется отношение активной мощности Р к полной мощности S:

.

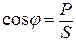Рассмотрим роль коэффициента мощности на примере.

Допустим, имеется источник питания, линия электропередач и потребитель (рис. 3.41).

Источник генерирует полную мощность 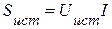, которая транспортируется вдоль линии электропередач (ЛЭП) к приемнику. В ЛЭП часть мощности теряется в виде потерь в линии 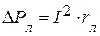. На вход приемника поступает полная мощность 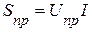. Вдоль линии имеет место падение напряжения 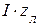и потеря напряжения .

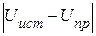В общем случае у потребителей преобладает активно-индуктивный характер нагрузки (электродвигатели переменного тока, трансформаторы и т.д.). Для нормальной работы предприятия требуется мощность, равная 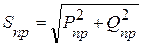, где 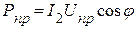, 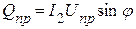. На входе предприятий или отдельных потребителей, необходимо устанавливать батарею конденсаторов. В этом случае коэффициент мощности на входе приемника увеличивается и можно добиться 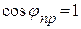. Тогда 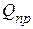приемника существенно уменьшиться и полная мощность будет соответственно равна 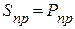. При неизменном напряжении в конце линии 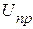ток в линии 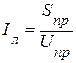уменьшится, что позволяет выбирать проводник линии меньшего сечения. В идеальном случае, при 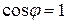, вдоль линии электропередач будет передаваться только активная мощность, а следовательно, вдоль ЛЭП можно пропустить большую активную мощность.

Рассмотрим влияние коэффициента мощности 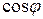на конкретном примере.

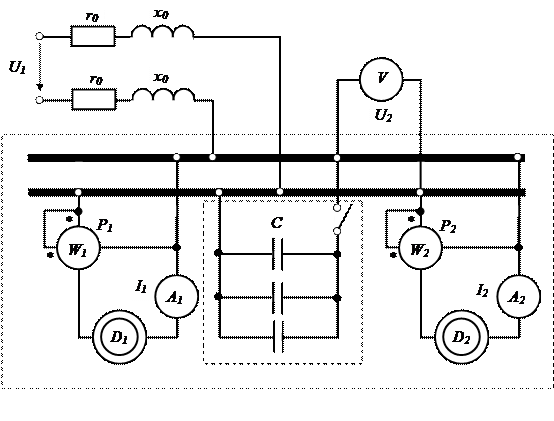
Пример 3.6. Два электродвигателя установки переменного тока Д₁ и Д₂ подключены параллельно к сети с напряжением U₂. Вся установка работает с низким коэффициентом мощности cosφ. Измерительные приборы в цепи каждого электродвигателя показывают токи I₁, I₂ и мощности Р₁, Р₂.

ЛЭП, снабжающая установку электроэнергией, имеет активное сопротивление R₀ и индуктивное X₀. Коэффициент мощности установки может быть повышен включению параллельно двигателю батареи конденсаторов.

Необходимо:

а) Рассчитать заданную электрическую цепь и определить (до подключ. конденс.):

1) ток в линии

2) напряжение в начале линии

3) потерю или падение напряжения в линии

4) активную и реактивную мощности и потери мощности в проводах

5) коэффициент мощности установки

6) К.П.Д. линии

б) Рассчитать величину емкости компенсирующей батареи конденсаторов для получения коэффициента мощности cosφ = 0,95 и мощности этой батареи. Выполнить расчет цепи при условии работы батареи конденсаторов и найти величины, указанные в пункте а). Построить векторную диаграмму напряжений и токов в конце линии.

Дано:

R₀ = 0,03 Ом I₁ = 100 A P₁ = 8 000 Вт U₂ = 127 В

X₀ = 0,05 Ом I₂ = 60 A P₂ = 6000 Вт

Решение:

Изобразим схему замещения электрической цепи:

Определим коэффициент мощности каждого двигателя:

P₁ = U₁I₁cosφ₁; => cosφ₁ = P₁ / U₁I₁ = 8000 / 127∙100 = 0,629

P₂ = U₂I₂cosφ₂; => cosφ₂ = P₂ / U₂I₂ = 6000 / 127∙60 = 0,787

Разложим токи на активные и реактивные составляющие:

I_1A = I₁∙ cosφ₁ = 100∙0,629 = 62,9 (A) I_1P = I₁∙sinφ₁ = 100∙0,777 = 77,7 (A)

I_2A = I₂∙ cosφ₂ = 60∙0,787 = 47,22 (A) I_2P = I₂∙sinφ₂ = 60∙0,615 = 36,9 (A)

Определим ток, потребляемый электродвигателями:

I = √(I_1A + I_2A)² + (I_1P + I_2P)² = √(62,9 + 47,22)² + (77,6 + 36,96)² = 158,9 (A)

Определим потерю напряжения в линии:

ΔU = 2R₀∙ (I_1A + I_2A) + 2X₀∙ (I_1P + I_2P) = 2∙0,03∙(62,9+47,22) + 2∙0,5∙(77,6+36,96) = 18,06 (B)

Вычислим напряжение в начале линии:

U = U₂ + ΔU = 127 + 18,06 = 145,06 (B)

Определим потери мощности в линии:

а) активные: ΔP = I²∙2R₀ = 158.9²∙2∙0,03 = 1514,95 (Вт)

б) реактивные: ΔQ = I²∙2X₀ = 158,9²∙2∙0,05 = 2524,92 (Вт)

Определим мощности в конце линии:

а) активная: P = P₁ + P₂ = 8000 + 6000 = 14000 (Вт)

б) реактивная: Q = I₁²∙Z₁∙sinφ₁ + I₂²∙Z₂∙sinφ₂

найдем полные сопротивления параллельных ветвей:

Z₁ = U₂ / I₁ = 127 / 100 = 1,27 (Ом)

Z₂ = U₂ / I₂ = 127 / 60 = 2,12 (Ом)

Q = 100²∙1,27∙0,776 + 60²∙2,12∙0,616 = 14556 (Вт)

в) полная: S = U₂∙I = 127∙158,9 = 20180,3 (Вт)

Определим коэффициент мощности до подключения батареи конденсаторов:

cosφ_СВ = P / S = 14000 / 20180,3 = 0,693; φ_CB = 46°

Определим КПД линии:

η = P / (P + ΔP) = 14000 / (14000 + 1514,95) = 0,902

По условию задачи после подключения батареи конденсаторов скомпенсированный коэффициент мощности должен быть равен 0,95

cosφ_K = 0,95 => φ_K = 18,19°

Вычислим емкость батареи конденсаторов для компенсации коэффициента мощности:

C_K = P∙(tgφ_СВ - tgφ_K) / (ω∙U₂²) = 14000∙(1,038 – 0,328) / (314∙127²) = 1,96∙10^-3 (Ф)

Определим мощность батареи конденсаторов:

Q_C = U₂² ∙ ωC = 127² ∙ 314∙1,96∙10^-3 = 9942,25 (Вт)

Найдем реактивное сопротивление батареи конденсаторов:

X_C = 1 / ωC = 1 / (314∙1,96∙10^-3) = 1,62 (Ом)

Определим реактивный ток батареи конденсаторов: I_C = U₂ / X_C = 127 / 1,62 = 78,28 (A)

Вычислим величину тока в линии после подключения конденсаторов:

I_K = √(I_1A + I_2A)² + (I_1P + I_2P – I_C)² = √(62,9 + 47,22)² + (77,6 + 36,96 – 78,28)² = 115,94 (A)

Потеря напряжения в линии после компенсации составит:

ΔU_K = 2R₀(I_1A + I_2A) + 2X₀(I_1P + I_2P – I_C) = 2∙0,03∙(62,9 + 47,22) + 2∙0,05∙(77,6 + 36,96 – 78,28) = 10,235 (B)

Тогда необходимое напряжение в начале линии после компенсации будет:

U_K = U₂ + ΔU_K = 127 + 10,235 = 137,235 (B)

Определим потери мощности в линии после компенсации:

ΔP_K = I_K² ∙ 2R₀ = 115,94² ∙ 2∙0,03 = 806,52 (Вт)

ΔQ_K = I_K² ∙ 2X₀ = 115,94² ∙2∙0,05 = 1344,2 (Вт)

Определим мощности в конце линии после компенсации:

а) активная: P_K = P = 14000 (Вт)

б) реактивная: Q_K = Q – Q_C = 14556 – 9942,25 = 4613,75 (Вт)

в) полная: S_K = U₂∙I_K = 127∙115,94 = 14724,38 (Вт)

Определим коэффициент мощности после компенсации:

cosφ = P_K / S_K = 14000 / 14724,38 = 0,9508

Определим КПД линии после компенсации:

η_K = P_K / (P_K + ΔP) = 14000 / (14000 + 806,52) = 0,946

Построим векторную диаграмму напряжений и токов в конце линии:

Результаты вычислений запишем в таблицу:

Режим работы	Коэфф. мощности в начале линии	Емкость батареи, мкф	Ток в линии, A	Напряжение в начале линии, B	Потеря напряжения в ЛЭП, %	Активная мощность в начале линии, Вт	Мощность потерь в ЛЭП, %	К.П.Д. ЛЭП	Реактивная мощность в конце ЛЭП, Вт
A	0,693		158,9	145,06	14,22		10,82	0,902
B	0,95	115,9	137,23	8,05	5,76	0,946

Пример 3.7. Двигатель мощность 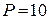кВт работает при напряжении 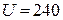В и частоте 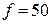Гц с 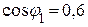. Определить емкость конденсатора, который нужно подключить параллельно двигателю, чтобы 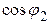установки повысить до значения 0,9.

Решение.

На рисунке 3.1 приведена схема замещения двигателя.

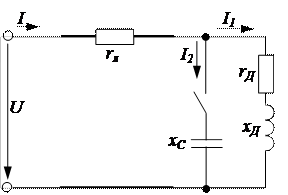
Рисунок 3._ – Схема замещения двигателя

1. Ток двигателя при коэффициенте мощности 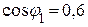равен:

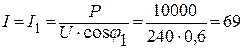А.

2. Реактивная составляющая тока двигателя

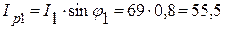А.

3. Если параллельно двигателю включен конденсатор при коэффициенте мощности 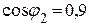, то ток в линии равен

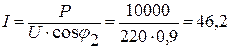А.

4. Реактивная составляющая тока двигателя при включенном конденсаторе

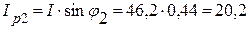А.

5. Реактивная составляющая тока при включенном конденсаторе соответственно равн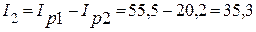а

А.

6. Сопротивление конденсатора и его емкость соответственно равны:

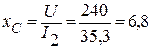Ом,

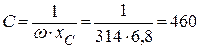мкФ.

Таким образом, параллельно двигателю должен быть включен конденсатор емкостью 460 мкФ.