2015-05-26
810
Синусоидальная величина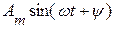 
может быть представлена в виде вектора, отложенного на комплексной плоскости. С этой целью под углом 
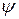против часовой стрелки (рис. 3.42) к оси действительных величин 
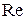, откладывают вектор, по величине равный амплитудному значению 
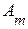(или действующему значению 
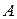). В результате получим вектор комплексной амплитуды 
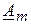(или вектор комплекса действующего значения 
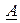) синусоидальной величины.
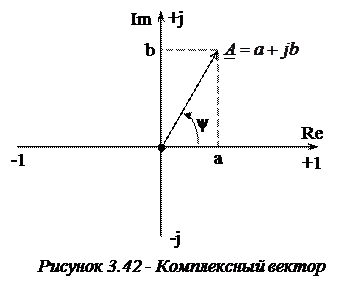
Таким образом, комплексный вектор 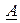(рис. 3.42) может быть представлен в показательной форме: 
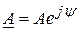. Такая форма записи дает полную информацию о синусоидальной величине.
Модуль соответствует действующему значению синусоидальной величины (ток, напряжение и др.), либо амплитудному значению .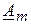
Аргумент 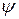представляет собой начальную фазу. При этом циклическая 
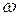частота постоянна. Если необходимо подчеркнуть величину циклической частоты 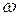, то комплексный вектор может быть записан в следующей форме:
.
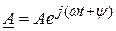Для действий над комплексными векторами, комплексный вектор может быть записан в алгебраической форме
,
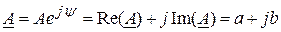где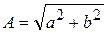 
,
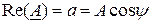- действительная часть комплексного вектора,
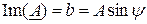- мнимая часть комплексного вектора.
