Резонанс токов. Резонанс токов можно наблюдать в цепи с параллельным соединением r, L, C

Резонанс токов можно наблюдать в цепи с параллельным соединением r, L, C. Рассмотрим идеальный контур (рис. 3.79):

Согласно условию резонанса: b = b_L - b_C = 0 => b_L = b_C.

Резонансная частота идеального контура: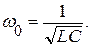

Вычертим векторную диаграмму (рис. 3.80):

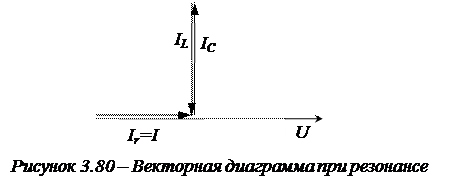
Токи в ветвях могут быть больше тока общего контура. При резонансе токов реактивная составляющая тока циркулирует внутри схемы (отсюда название резонанса токов).

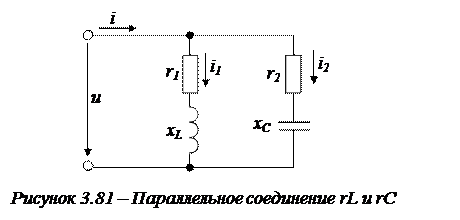Рассмотрим условие резонанса в реальной цепи (рис. 3.81) с параллельным соединением rL и rC.

Реактивные проводимости параллельных ветвей.

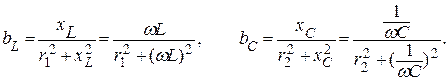
При 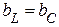противоположные по фазе реактивные составляющие токов равны.

Так как по условия резонанса b_L = b_C, то

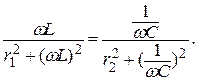
Если решить это уравнение относительно w, то мы можем получить выражение для w_р:

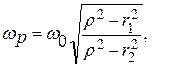где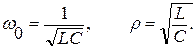

Резонанс в этом случае возможен, когда:

r₁ > r и r₂ > r, или r₁ < r и r₂ < r.

Если r₁ = r₂ = r, то резонанс имеет место при всех частотах.

Если r₁ = r₂, то w = w_о.

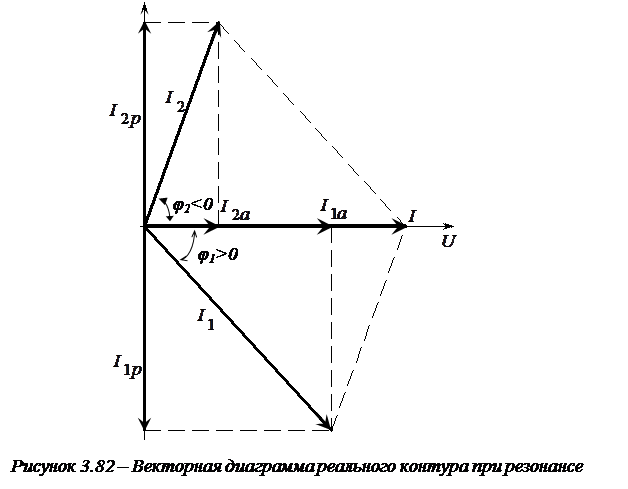
Таким образом, при резонансе токов, т.к. b_L = b_C, то реактивные составляющие токов равны между собой .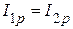

Следовательно, ток в неразветвленном участке цепи

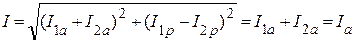
будет иметь чисто активный характер. При этом угол сдвига фаз между токов и напряжением φ=0.