Запишем комплексные значения токов 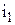 ,
, 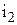 ,
, 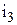 , в показательной форме:
, в показательной форме:
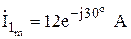 ;
;
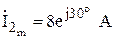 ;
;
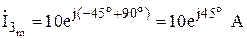 .
.
Дополнительные 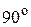 в показателе дает функция косинуса, так как косинус опережает синус на
в показателе дает функция косинуса, так как косинус опережает синус на 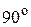 .
.
Запишем эти комплексы в тригонометрической форме и перейдем к алгебраической форме.
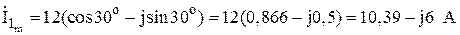 ;
;
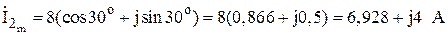 ;
;
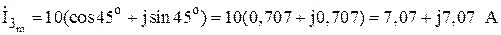 .
.
Найдем комплекс общего тока 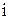 , как сумму трех токов; складывать комплексы лучше в алгебраической форме записи.
, как сумму трех токов; складывать комплексы лучше в алгебраической форме записи.
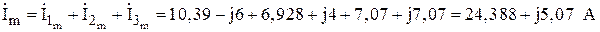 ;
;
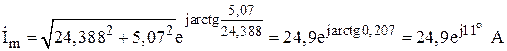 .
.
Запишем ток 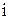 в мгновенной форме записи:
в мгновенной форме записи:
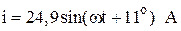 .
.
Построим векторные диаграммы токов 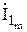 ,
, 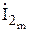 ,
, 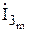 ,
, 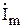 (рис. 7).
(рис. 7).
Таблица 2
| № вар-та | 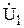 | 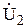 | 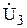 |
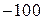 | 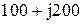 | 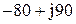 | |
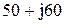 | 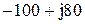 | 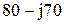 | |
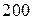 | 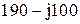 | 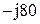 | |
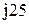 | 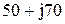 | 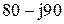 | |
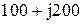 | 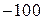 | 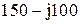 | |
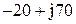 | 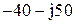 | 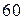 | |
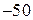 | 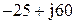 | 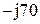 | |
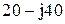 | 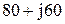 | 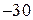 | |
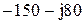 | 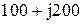 | 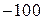 | |
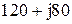 | 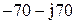 | 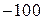 | |
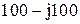 | 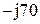 | 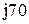 | |
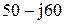 |  | 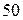 | |
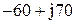 | 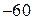 | 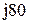 | |
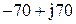 | 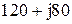 | 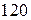 | |
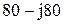 | 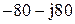 | 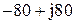 | |
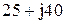 | 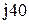 | 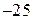 | |
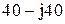 | 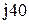 | 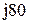 | |
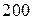 | 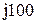 | 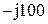 | |
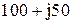 | 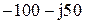 | 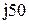 | |
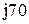 | 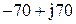 | 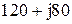 | |
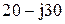 | 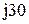 | 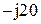 | |
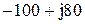 | 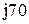 | 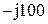 | |
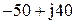 | 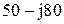 | 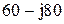 | |
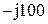 | 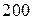 | 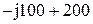 | |
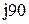 | 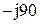 | 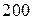 | |
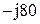 | 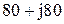 | 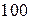 | |
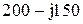 | 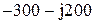 | 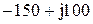 | |
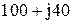 | 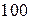 | 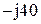 | |
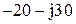 | 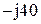 | 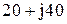 | |
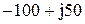 | 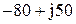 | 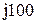 | |
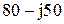 | 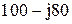 | 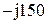 | |
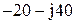 | 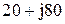 | 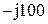 |
Сделаем проверку: общий ток 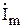 должен быть геометрической суммой токов
должен быть геометрической суммой токов 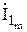 ,
, 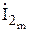 ,
, 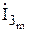 .
.
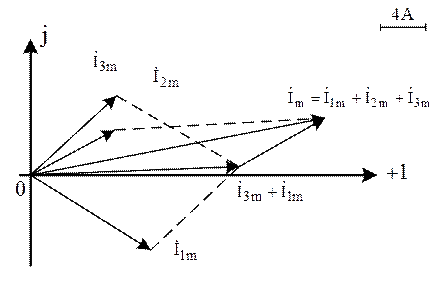
Рис. 7
Построим временную диаграмму тока 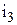 (рис. 8).
(рис. 8).
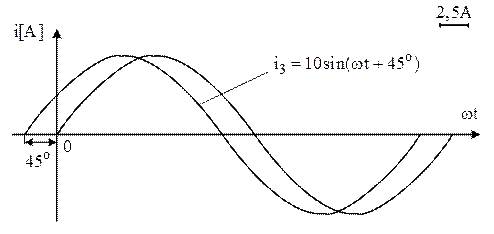
Рис. 8
При выполнение контрольного задания данные для задачи взять из таблицы 3.
Таблица 3
| № вар-та | 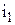 | 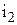 | 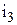 |
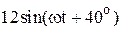 | 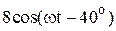 | 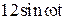 | |
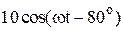 | 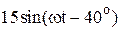 | 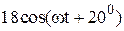 | |
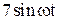 | 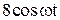 | 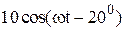 | |
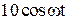 | 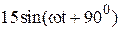 | 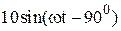 | |
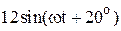 | 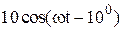 | 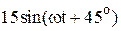 | |
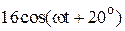 | 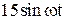 | 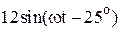 | |
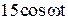 | 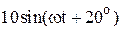 | 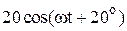 | |
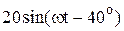 | 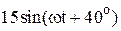 | 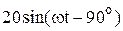 | |
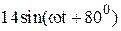 | 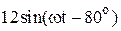 | 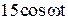 | |
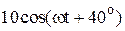 |  |  | |
 |  |  | |
 |  |  | |
 |  |  | |
 | 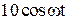 | 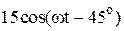 | |
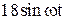 | 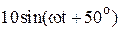 | 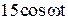 | |
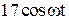 | 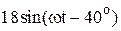 | 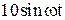 | |
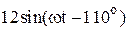 | 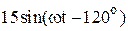 | 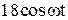 | |
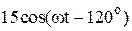 | 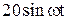 | 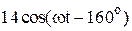 | |
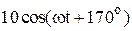 | 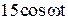 | 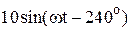 | |
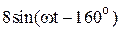 | 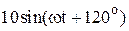 | 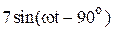 | |
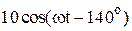 | 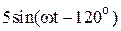 | 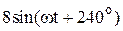 | |
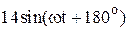 | 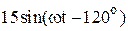 | 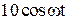 | |
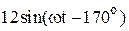 | 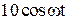 | 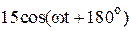 | |
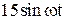 | 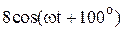 | 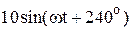  | |
 |  |  | |
 | 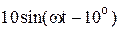 | 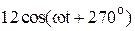 | |
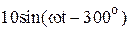 | 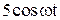 | 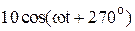 | |
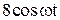 | 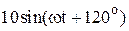 | 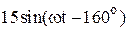 | |
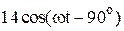 | 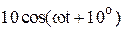 | 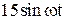 | |
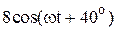 | 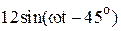 | 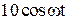 | |
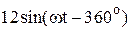 | 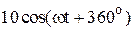 | 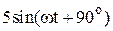 | |
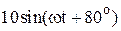 | 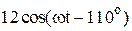 | 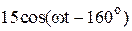 |
|
|
|
 2015-05-26
2015-05-26 2234
2234
