1. Уравнение Максвелла в интегральной форме.
2. Уравнение Максвелла в дифференциальной форме.
3. Синусоидальное электромагнитное поле.
4. Уравнение Максвелла в комплексной форме
Краткое содержание лекции
Первое уравнение Максвелла – это известный закон полного тока Ампера, к которому Максвелл добавил ток смещения, вектор плотности которого равен:
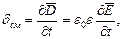
поэтому первое уравнение Максвелла имеет вид
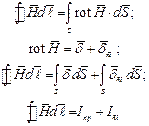
Здесь 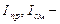 токи проводимости и смещения.
токи проводимости и смещения.
В левой части первого уравнения Максвелла стоит контурный интеграл по замкнутой линии, в правой части стоят интегралы от плотности токов проводимости и смещения, они берутся по любой поверхности, ограниченной контуром.
Если произвести следующие операции:
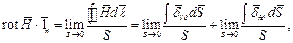
где 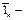 единичный вектор нормальный к поверхности
единичный вектор нормальный к поверхности 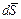 , то получим
, то получим
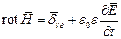
| (1) |
Это и есть первое уравнение Максвелла, записанное в дифференциальной форме (индекс у 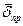 обычно опускается):
обычно опускается):
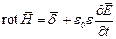 или
или 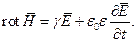
Второе уравнение Максвелла – это известный закон электромагнитной индукции, или уравнение Максвелла-Фарадея: э.д.с.,наводимая в замкнутом контуре изменяющимся магнитным полем, равна скорости изменения магнитного потока, сцеплённого с контуром:
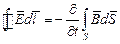
| (2) |
Используя также операцию ротора, преобразуем (2) в дифференциальную форму:
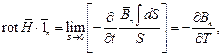
где 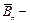 среднее по поверхности S значение нормальной составляющей индукции.
среднее по поверхности S значение нормальной составляющей индукции.
В результате имеем дифференциальную форму записи закона Максвелла в дифференциальной форме:
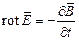 или
или 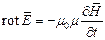
Эти два уравнения дополняются соотношениями:
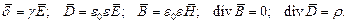
В практике электромеханики электромагнитное поле чаще всего бывает синусоидальным. Для вектора, величина которого изменяется синусоидально, можно записать:
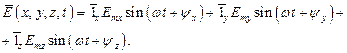
| (3) |
Каждая проекция вектора (3) изменяется по синусоидальному закону со своей начальной фазой. Поэтому вектор в пространстве описывает сложную фигуру (эллипсоид). Преобразуем (3) в комплексную форму.
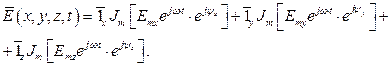
Обозначим 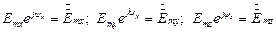 , то есть в результате получаем комплексные амплитуды.
, то есть в результате получаем комплексные амплитуды.
Удобнее оперировать не комплексными амплитудами, а комплексными действующими значениями:
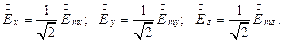
Тогда можно записать вектор в комплексной форме:
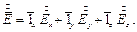
Уравнения Максвелла в комплексной форме приобретут следующую форму:
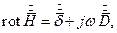
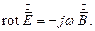
Энергия поля и её преобразование
Вектор потока мощности называется вектором Пойнтинга иравен:
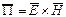
Анализ преобразования энергии в электромагнитном поле можно основывать на теореме Умова, соответствующей закону сохранения энергии и представлением о её физической локализации: если внутри некоторого объёма V происходит изменение энергии, то через замкнутую поверхность, охватывающую объём, должен пройти поток энергии равный этому изменению.
Переходя от энергии к мощности, можно теорему формулировать так: скорость уменьшения энергии 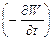 , заключённой в объёме V, равна потоку мощности, который выходит через поверхность, охватывающую этот объём, то есть:
, заключённой в объёме V, равна потоку мощности, который выходит через поверхность, охватывающую этот объём, то есть:
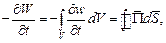
| (4) |
здесь буквой 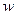 обозначена объёмная плотность энергии. Применяя к формуле (1) теорему Остроградского-Гаусса, можно записать теорему Умова в дифференциальной форме:
обозначена объёмная плотность энергии. Применяя к формуле (1) теорему Остроградского-Гаусса, можно записать теорему Умова в дифференциальной форме:
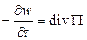
| (5) |
Эту теорему предложил профессор МГУ Умов Н.А. в своей докторской диссертации (1874) для механики сплошных сред, а через 10 лет аналогичная теорема была доказана в Англии Пойнтингом и Хевисайдом (независимо друг от друга и от работ Умова) для энергии электромагнитного поля.
Запишем систему уравнений Максвелла и умножим первое уравнение на 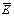 , а второе на
, а второе на 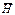 :
:

Вычтем из первого второе уравнение:
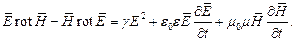
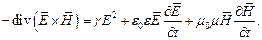
Интегрируя по объёму V, получаем:
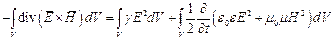
или
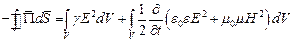
Формулировка теоремы Пойнтинга следующая: сумма скорости, с которой возрастает энергия электромагнитного поля внутри некоторого объёма, и скорости, с которой часть энергии электромагнитного поля внутри объёма в неэлектромагнитные виды энергии, равна потоку мощности электромагнитного поля, входящего через замкнутую поверхность S, ограничивающую этот объём.
Скорость возрастания энергии поля равен:
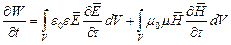 ,
,
а скорость изменения энергии, преобразованной в тепло
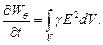
В случае линейной цепи с сосредоточенными параметрами 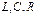 :
:
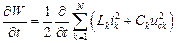
и
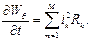
Теорема Пойнтинга остаётся справедливой при всех видах преобразования электромагнитной энергии.
 2014-02-02
2014-02-02 495
495








