1) 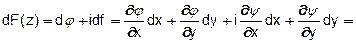
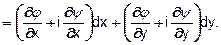
2) Выносим во второй скобке множитель i за знак скобки. Используем соотношения Коши-Римана 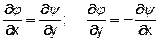 ®
® 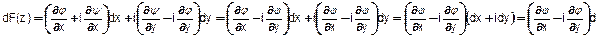
т.е. 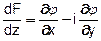 .
.
3) Т.к. 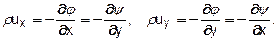 имеем
имеем 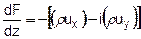
4) 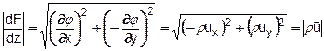
|
10. Доказать, что характеристическая функция F(z) = Az описывает прямолинейно-параллельное течение. Найти массовую скорость.
1) А = А1 + iA2 2) 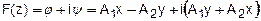
3) потенциальная функция jи функция тока y 
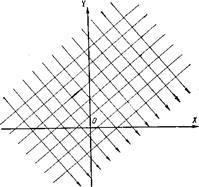
4) семейство эквипотенциальных линий: А1х – А2y = С — эквипотенциальные линии - прямые с угловым коэффициентом A1/А2.
5) семейство линий тока: А1у + А2х = С** — линии тока – прямые с угловым коэффициентом (- A2А1 ).
|
11. Доказать, что характеристическая функция F(z) = Alnz описывает плоскорадиальное течение. Найти массовую скорость.
1) z = х +i y = r (cos θ + i sin θ ) = rei θ
2) F(z) = A In (reiθ) = A In r + iA θ.
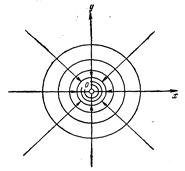
3) j=Alnr; y=A θ. Уравнения эквипотенциальных линий – ν =const: концентрические окружности с центром в начале координат. Уравнения линии тока – θ = const: прямые, проходящие через начало координат.
4) Массовая скорость равна производной от характеристической функции 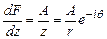 . Эта производная – комплексное переменное, модуль которого равен массовой скорости и представляет собой множитель перед е-i θ.Следовательно
. Эта производная – комплексное переменное, модуль которого равен массовой скорости и представляет собой множитель перед е-i θ.Следовательно 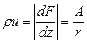 .
.
5) Для плоскорадиального потока 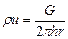 ,
, 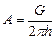 ,
, 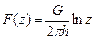
|
 2015-05-29
2015-05-29 631
631








