Деление комплексных чисел

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Составим частное:
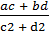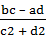+ i

2. Тригонометрическая форма записи

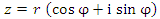
r - абсолютная величина комплексного числа z
.

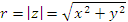φ - аргумент комплексного числа z

.

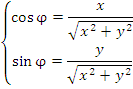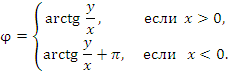
Если комплексные числа z ₁ и z ₂ представлены в тригонометрической форме, то z ₁ = z ₂ тогда и только тогда, когда | z ₁ | = | z ₂ |

Абсцисса a и ордината b комплексного числа a + b·i выражаются через модуль r и аргумент φ формулами: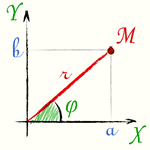

a = r·cos (φ)

b = r·sin (φ)

Поэтому всякое комплексное число можно представить в виде:
a + b·i = r· (cos (φ)+ i·sin (φ))

3. Показательная форма

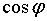и 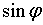связаны формулой Эйлера: ,

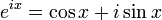Пусть 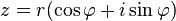, тогда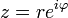

в тригонометрической форме , .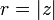

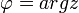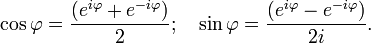
4. Возведение комплексных чисел в степень

При возведении комплексного числа в любую целую степень модуль комплексного числа возводится в ту же степень, а аргумент умножается на показатель степени.

(a + i b)²= (r (cos (φ)+ i·sin (φ)))²= r ²(cos (2 φ)+ i·sin (2 φ))

(a + i b)³= (r (cos (φ)+ i·sin (φ)))³= r ³(cos (3 φ)+ i·sin (3 φ))