2015-05-30
2910
· Сходящаяся последовательность — это последовательность элементов множества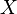 
, имеющая предел в этом множестве.
· Расходящаяся последовательность — это последовательность, не являющаяся сходящейся.
11. Понятие окрестности точки. Точка сгущения последовательности.
Окрестность точки — множество, содержащее данную точку, и близкие к ней.
Точка сгущения - точка, в любой окрестности которой имеются точки рассматриваемого множества, отличные от нее.
12. Бесконечно малые и бесконечно большие последовательности.
Последовательность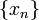 
называется бесконечно большой, если для любого положительного числа A можно указать номер N такой, что при 
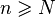все элементы 
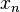этой последовательности удовлетворяют неравенству 
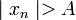. Любая бесконечно большая последовательность является неограниченной. Но не каждая неограниченная последовательность является бесконечно большой.
Последовательность 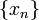называется бесконечные малой, если для любого положительного числа ε можно указать номер N такой, что при 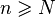все элементы 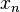этой последовательности удовлетворяют неравенству 
.
|
|
|
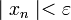13. Монотонные последовательности.
Монотонная последовательность - строго возрастающая или строго убывающая последовательность
Последовательность 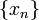не возрастает(не убывает), если 
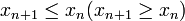для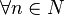 
Последовательность 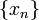возрастает (убывает), если 
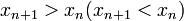для .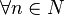
14. Точные грани последовательности.
Пусть дано частично упорядоченное множество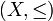 
и его подмножество 
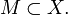Тогда элемент 
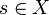называется точной верхней гранью или супремумом 
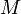, если он является наименьшей верхней гранью 
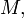то есть
§ 
§ 
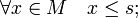
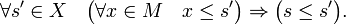
Аналогично элемент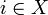 
называется точной нижней гранью или инфимумом 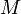, если он является наибольшей нижней гранью 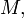то есть
§ 
§ 
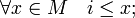
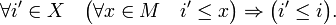
Пишут:
§ 
§ 
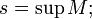
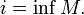
15. Число e (основные положения доказательства).
e — математическая константа, основание натурального логарифма, трансцендентное число.
· Число e является вычислимым (а значит, и арифметическим) числом.
· 
· 
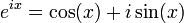
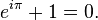
· предел
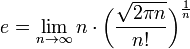
· Для любого комплексного числа z верны следующие равенства:
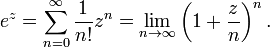
§ Число e разлагается в бесконечную цепную дробь
§ 
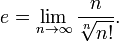
16. Предел функции в точке. Односторонние пределы.
