Преобразование поворота

Ранее рассмотренная для двумерного случая матрица поворота является в то же время трехмерным поворотом вокруг оси Z. Так как при трехмерном повороте вокруг оси Z (поворот в плоскости XY) размеры вдоль оси Z неизменны, то все элементы третьей строки и третьего столбца равны 0, кроме диагонального, равного 1:

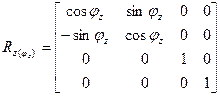
При повороте вокруг оси X (в плоскости YZ) размеры вдоль оси X не меняются, поэтому все элементы первой строки и первого столбца равны 0, за исключением диагонального, равного 1:

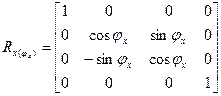
При повороте вокруг оси Y (в плоскости XZ) размеры вдоль оси Y не меняются, поэтому все элементы второй строки и второго столбца равны 0, за исключением диагонального, равного 1:

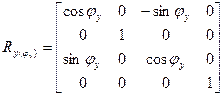
Столбцы и строки подматриц 3×3 матриц поворота Rx, Ry, Rz, аналогично двумерному случаю, представляют собой взаимно ортогональные единичные векторы. Легко убедиться, что суммарная матрица преобразования для произвольной последовательности поворотов вокруг осей X, Y и Z имеет вид:

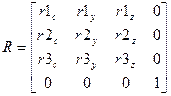
причем столбцы (и строки) представляют собой взаимно ортогональные единичные векторы.

Зеркальное отображение:

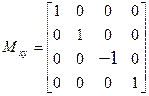
Аффинные преобразования: вращение, дилатация (растяжение, сжатие), отражение и перенос — часто используются в качестве механизма порождения новых фигур из исходных. Способом описания, позволяющим единым образом представить все указанные преобразования и, широко используемым в компьютерной графике, являются однородные координаты. Они вводятся следующим образом в пространстве. Пусть точка имеет декартовы координаты (x,y,z), тогда её однородными координатами называется четвёрка чисел (hx, hy, hz) при 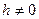. Фиксированной точке пространства при этом ставится в соответствие множество четвёрок однородных координат с различными 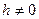. Если 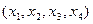— однородные координаты точки, то её декартовы координаты вычисляются согласно определению

, ,

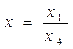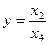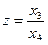
Однородные координаты позволяют единым образом представить все аффинные преобразования в пространстве и различные типы проектирования.

Для описания аффинных преобразований достаточно рассмотреть случай, когда 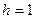и каждая точка описывается четвёркой однородных координат вида (x,y,z,1). При преобразованиях точка с однородными координатами (x,y,z,1) переходит, в общем случае, в новую точку с однородными координатами 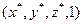, которые находятся с помощью матричного умножения:

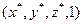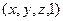= [A].

Рассмотрим теперь, какие матрицы отвечают аффинным преобразованиям в пространстве и могут использоваться в качестве матрицы [A].

Матрицы вращения (Rotation):

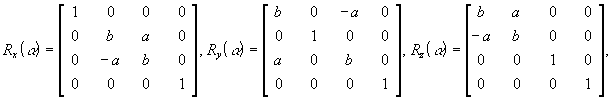
где а =sina, b =соsa. Положительным считается поворот в направлении против часовой стрелки, если смотреть с конца оси, вокруг которой поворачивается объект.

Матрица дилатации (Dilatation):

[D()]=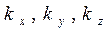

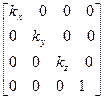
зависит от трёх параметров 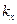, , 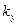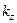>0 — коэффициентов сжатия-растяжения вдоль соответствующих осей. При 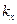<1 — сжатие вдоль оси x, при 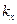>1 — растяжение. Аналогично для , .

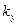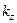Матрицы отражения (Reflection, Mirror):

— относительно плоскости xy:

[ ]= ;

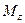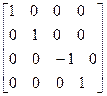— относительно плоскости yz:

[ ]= ;

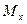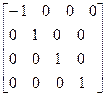— относительно плоскости zx:

[ ]= ;

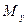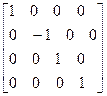Матрицы переноса (Translation):

[ ]=

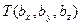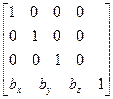
соответствует параллельному переносу на вектор .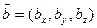

Приведённые матрицы представляют элементарные аффинные преобразования. Для общих аффинных преобразований в пространстве матрица [A] формируется последовательным перемножением соответствующих матриц. В порядке, в котором производятся преобразования, слева направо.

Основные преобразования координат

Рассмотрим некоторую декартову систему координат. Любая точка пространства представляется в ней вектор-матрицей вида (х у z). Мы будем пользоваться однородными координатами точки в пространстве (х у z 1).

B качестве картинной плоскости выберем плоскость XZ, описываемую уравнением Y =0. Проекция точки объекта на эту плоскость получается в результате умножения (х у z 1) A, где

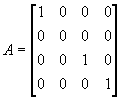
задает преобразование проецирования на плоскость XZ.

Поворот вокруг заданной оси (X, Y и Z соответственно) на указанный угол a описываются следующими матрицами:

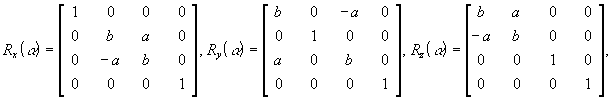
где а =sina, b =соsa. Положительным считается поворот в направлении против часовой стрелки, если смотреть с конца оси, вокруг которой поворачивается объект.

Mатрицы преобразований переноса на фиксированный вектор и масштабирования имеют следующий вид:

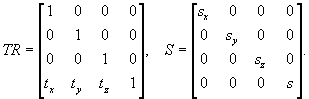
Здесь (t_x, t_y, t_z) – вектор переноса; s_x, s_y, s_z - масштабные множители вдоль осей X, Y и Z соответственно, 1/ s – множитель общего масштабирования.

10. Аффинные преобразования, их свойства и инварианты.

Линейное преобразование на плоскости

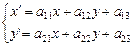(1)

называется ортогональным, если выполняются соотношения

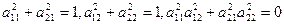(2)

Из соотношений (2) следует, что

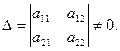(3)

Поэтому ортогональное преобразование всегда является аффинным. Докажем основное свойство ортогональных преобразований.

Теорема. При ортогональных преобразованиях сохраняются расстояния между точками

Преобразование на плоскости можно рассматривать как движение этой плоскости. При движении ортогональная система координат переходит в ортогональную систему координат. Этим можно объяснить термин ортогональное преобразование.

Ортогональные преобразования обладают следующими свойствами:

1 ^о. Последовательное выполнение двух ортогональных преобразований есть ортогональное преобразование.

2°. Тождественное преобразование х' = х, у' = у является ортогональным преобразованием (для этого преобразования соотношения (2), очевидно, выполняются).

3°. Преобразование, обратное ортогональному, также является ортогональным.

Линейное преобразование в пространстве

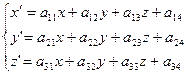(4)

называется ортогональным, если выполняются соотношения

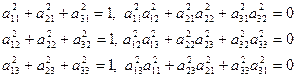(5)

Ортогональное преобразование является аффинным. Справедливо следующее основное свойство ортогональных преобразований: при таких преобразованиях сохраняются расстояния между точками.

Ортогональные преобразования в пространстве обладают следующими свойствами.

1 ^о. Последовательное выполнение ортогональных преобразований является ортогональным преобразованием.

2°. Тождественное преобразование x' = x, y' = y, z' = z — ортогональное преобразование.

3°. Преобразование, обратное ортогональному, также ортогональное.