Обратимся теперь к трехмерному случаю (3D) (3-dimension) и начнем наши рассмотрения сразу с введения однородных координат.
Поступая аналогично тому, как это было сделано в 2D, заменим координатную тройку (х, у, z), задающую точку в пространстве, на четверку чисел (х y z 1) или, более обще, на четверку (hx hy hz), h ¹ 0.
Каждая точка пространства (кроме начальной точки О) может быть задана четверкой одновременно не равных нулю чисел; эта четверка чисел определена однозначно с точностью до общего множителя.
Предложенный переход к новому способу задания точек дает возможность воспользоваться матричной записью и в более сложных, трехмерных задачах.
Любое аффинное преобразование в трехмерном пространстве может быть представлено в виде суперпозиции вращении, растяжений, отражений и переносов. Поэтому вполне уместно сначала подробно описать матрицы именно этих преобразований (ясно, что в данном случае порядок матриц должен быть равен четырем).
А. Матрицы вращения в пространстве
Матрица вращения вокруг оси абсцисс на угол j:
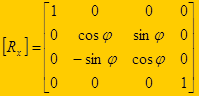
Матрица вращения вокруг оси ординат на угол y:

Матрица вращения вокруг оси аппликат на угол c:
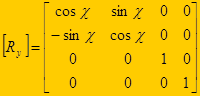
Замечание
Полезно обратить внимание на место знака "-" в каждой из трех приведенных матриц.
Б. Матрица растяжения (сжатия):
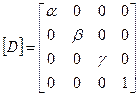
где
a > О - коэффициент растяжения (сжатия) вдоль оси абсцисс;
b > 0 - коэффициент растяжения (сжатия) вдоль оси ординат;
g > 0 - коэффициент растяжения (сжатия) вдоль оси аппликат).
В. Матрицы отражения
Матрица отражения относительно плоскости ху.
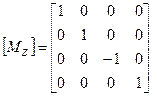
Матрица отражения относительно плоскости уz:
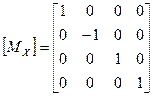
Матрица отражения относительно плоскости zx:
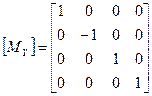
Матрица переноса (здесь (l, m, n) - вектор переноса):
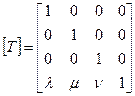
 2015-05-30
2015-05-30 1752
1752








