Замечание. Как и в двумерном случае, все выписанные матрицы невырождены

Как и в двумерном случае, все выписанные матрицы невырождены.

Приведем важный пример построения матрицы сложного преобразования по его геометрическому описанию.

Пример 1

Построить матрицу вращения на угол j вокруг прямой L, проходящей через точку А(а, b, с) и имеющую направляющий вектор (l, т, п). Можно считать, что направляющий вектор прямой является единичным:

l² +m²+n²=1

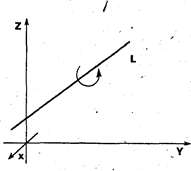
Рис. 10

На рис. 10 схематично показано, матрицу какого преобразования требуется найти.

Решение сформулированной задачи разбивается на несколько шагов. Опишем последовательно каждый из них.

1-й шаг. Перенос на вектор -А(-а, -Ь, -с) при помощи матрицы

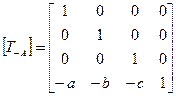
В результате этого переноса мы добиваемся того, чтобы прямая L проходила через начало координат.

2-й шаг. Совмещение оси аппликат с прямой L двумя поворотами вокруг оси абсцисс и оси ординат.

1-й поворот - вокруг оси абсцисс на угол y (подлежащий определению). Чтобы найти этот угол, рассмотрим ортогональную проекцию L' исходной прямой L на плоскость Х = 0 (рис.' 11).

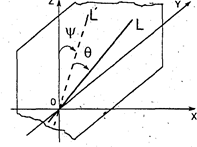
Рис. 11

Направляющий вектор прямой L' определяется просто - он равен

(0, m, n).

Отсюда сразу же вытекает, что

cos y = n/d, sin y = m/d

где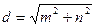

Соответствующая матрица вращения имеет следующий вид:

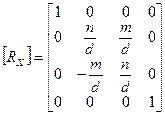
Под действием преобразования, описываемого этой матрицей, координаты вектора (l, m, п) изменятся. Подсчитав их, в результате получим

(l, m, n, 1)[R_X] =(l, 0, d, 1).

2-й поворот - вокруг оси ординат на угол q, определяемый соотношениями

cos q = l, sinq = -d.

Соответствующая матрица вращения записывается в следующем виде:

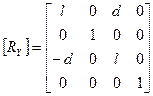
3-й шаг. Вращение вокруг прямой L на заданный угол j.

Так как теперь прямая L совпадает с осью аппликат, то соответствующая матрица имеет следующий вид:

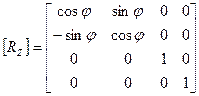
4-й шаг. Поворот вокруг оси ординат на угол -q.

5-й шаг. Поворот вокруг оси абсцисс на угол -y.