Уравнение линейной регрессии

Парная регрессия представляет собой регрессию между двумя переменным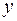и – и 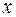, т. е. модель вида:

,

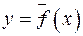где 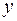– зависимая переменная (результативный признак); 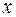– независимая, или объясняющая, переменная (признак-фактор). Знак «^» означает, что между переменным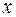и и 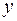нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина 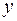складывается из двух слагаемых:

,

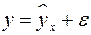где 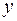– фактическое значение результативного признака; 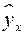– теоретическое значение результативного признака, найденное исходя из уравнения регрессии; 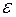– случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.

Случайная величина 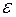называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.

Простейшая модель парной регрессии – линейная регрессия.

Линейная регрессия сводится к нахождению уравнения вида

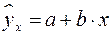или 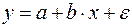. Уравнение вида 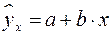позволяет по заданным значениям фактора 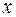находить теоретические значения результативного признака, подставляя в него фактические значения фактора .

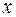Построение линейной регрессии сводится к оценке ее параметров – 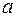и 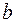. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров 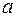и 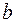, при которых сумма квадратов отклонений фактических значений результативного признака 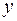от теоретических 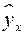минимальна.

Параметр 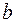называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Формально 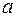– значение 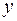при 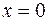. Если признак-фактор 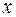не может иметь нулевого значения, то вышеуказанная трактовка свободного члена 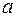не имеет смысла, т.е. параметр 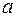может не иметь экономического содержания.