В данной работе “мертвое” время определяется методом нескольких источников. Суть метода состоит в следующем. Пусть, регистрация излучения некоторого источника осуществляется в течение времени Т. Пусть за это время было зарегистрировано m частиц. Тогда скорость счета равна:
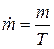 (1)
(1)
Понятно, что m - не истинное число частиц, прошедших за время Т через счетчик, поскольку после регистрации каждой частицы следует “мертвое” время, в течение которого другие частицы не фиксируются. Обозначим через n истинное число частиц, прошедших за время Т через счетчик. Тогда число частиц, прошедших через счетчик в единицу времени:
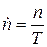 (2)
(2)
Определим число незарегистрированных частиц. Если через t обозначить “мертвое” время, то суммарное “мертвое” время за промежуток Т равно mt (т.к. после регистрации каждой из m частиц следует “мёртвое” время t). За время mt через счетчик пройдет 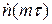 частиц. Таким образом истинное число частиц, прошедших за время Т равно:
частиц. Таким образом истинное число частиц, прошедших за время Т равно: 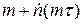 или тоже самое для n:
или тоже самое для n:
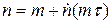 (3)
(3)
|
|
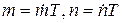 . Подставим эти выражения в (3) и сократим обе части равенства на Т:
. Подставим эти выражения в (3) и сократим обе части равенства на Т:
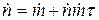 (4)
(4)
Отсюда находим связь между истинной 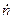 и наблюдаемой
и наблюдаемой 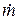 скоростями счета:
скоростями счета:
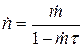 (5)
(5)
Предположим, что имеются два источника с истинными скоростями счета 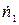 и
и 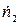 . Наблюдаемые скорости счета равны соответственно
. Наблюдаемые скорости счета равны соответственно 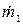 и
и 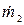 . Из (5) следует:
. Из (5) следует:
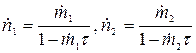 (6)
(6)
Если одновременно работают оба источника, то связь между истинной 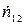 и наблюдаемой
и наблюдаемой 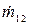 скоростями счета дается тем же выражением (5):
скоростями счета дается тем же выражением (5):
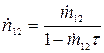 (7)
(7)
Очевидно, что 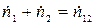 (однако неверно утверждение, что
(однако неверно утверждение, что 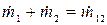 ). Подставив в это выражение в формулы (5), (6) получим:
). Подставив в это выражение в формулы (5), (6) получим:
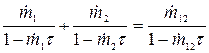 (8)
(8)
Воспользуемся тем, что обычно 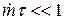 . Тогда
. Тогда 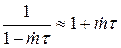 и формула (8)принимает вид:
и формула (8)принимает вид:
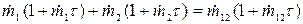
Отсюда окончательно:
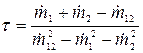 (9)
(9)
Таким образом, для нахождения “мертвого” времени необходимо определить наблюдаемые скорости счета первого 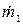 и второго
и второго 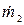 источников, а также обоих источников одновременно
источников, а также обоих источников одновременно 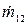 .
.
 2015-05-30
2015-05-30 330
330









