Интегрирование по частям

Способ основан на известной формуле производной произведения:

(uv)¢ = u¢v + v¢u

где u и v – некоторые функции от х.

В дифференциальной форме: d(uv) = udv + vdu

Проинтегрировав, получаем: 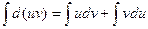, а в соответствии с приведенными выше свойствами неопределенного интеграла:

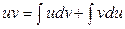или .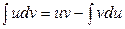

Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.

Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям:

А). Интегралы вида 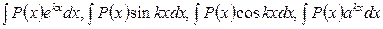, где Р(х) – многочлен, k – число. Удобно положить u=P(x), а за dv обозначить все остальные сомножители.

Б). Интегралы вида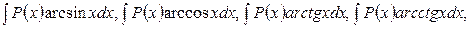

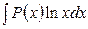. Удобно положить dv =P(x)dx, а за u обозначить остальные сомножители.

Пример.

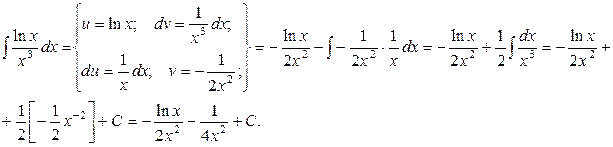
Пример.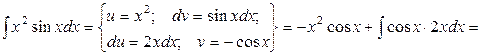

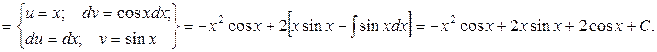
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.