Математическим маятником называется материальная точка, подвешенная на невесомой и нерастяжимой нити

Из соотношений для физического маятника можно получить аналогичное соотношение для математического маятника, в качестве которого часто рассматриваются некоторые физические маятники, например, шар, закрепленный на конце стержня длиной 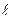. Так как момент инерции математической точки 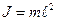, то имеем

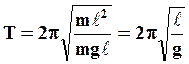. (35)

Период Т не зависит от массы m, а при малых α не зависит от амплитуды.

Заметим, что под 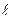понимается расстояние от точки «подвеса» системы до ее центра масс

Полная энергия гармонических колебаний постоянна и пропорциональна произведению массы, квадратов частоты и амплитуды

.

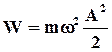Действительно

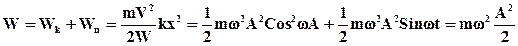
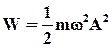. (36)