Цель работы: (переписывается из инструкции).
Далее следуют рабочие формулы, схемы, несложные рисунки, комментирующие записи, решения предлагаемых задач. Допустимы письменные ответы на контрольные вопросы, которыми можно пользоваться при беседе.
~~~~~~~~~~~~~~~~~~~~~~
3. ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
Выполнение каждой работы можно разделить на три этапа: 1) домашняя подготовка; 2) лабораторные измерения; 3) обработка результатов.
Домашняя подготовка включает в себя знакомство с содержанием работы по «методическим указаниям», просмотр соответствующих разделов учебника и подготовительные записи в рабочей тетради: дату выполнения, название и цель работы, базовые формулы, схемы. Обязательно должны быть решения в рабочей тетради предлагаемых расчётных задач, или хотя бы значительной их части. В тетради могут быть и письменные ответы на некоторые контрольные вопросы, если студент затрудняется запомнить их устно. Домашняя подготовка обычно занимает от 3 до 6 часов.
Качество домашней подготовки оценивается преподавателем на предварительной беседе при допуске к лабораторным измерениям.
Лабораторные измерения. Каждая работа в лаборатории выполняется индивидуально и, как правило, включает в себя самостоятельную сборку схемы или всей установки из элементов. Время выполнения работы (только сборка схемы и измерения, но без обработки результатов) – обычно 2-3 часа. Впрочем, выровнять все работы по «трудности» и по «временным затратам» не удаётся: некоторые работы выполняются за полтора-два часа, а для некоторых и четырёх мало.
В случае сомнительности результатов преподаватель вправе потребовать от студента повторить отдельные измерения в его (преподавателя) присутствии. После окончания измерений их результаты должны быть заверены подписью преподавателя в рабочей тетради студента.
Обработка результатов включает в себя расчёты, иногда довольно сложные, и построение графиков. Завершённая работа представляется преподавателю (обычно на следующем занятии, но иногда удаётся и в это же). Отчётная беседа − это обсуждение численных и графических результатов работы с выставлением общей оценки.
Как отмечалось, общая оценка работы определяется: 1) уровнем домашней подготовки (при допуске к лабораторному выполнению), 2) правильностью результатов и компетентностью при их обсуждении и 3) качеством оформления работы в тетради.
~~~~~~~~~~~~~~~~~~~~~~~~
Несколько общих советов, а точнее – требований по представлению результатов измерений и вычислений.
1. Запись чисел. Измеряемые величины обычно содержат от двух до четырёх значащих цифр. Расчётные величины должны представляться, как правило, с тремя цифрами. Иногда удаётся получить четыре, а иногда приходится довольствоваться двумя. Число значащих цифр в результате студент должен уметь обосновать, а не писать, «сколько даёт калькулятор». Если цифр записано меньше, чем дали измерения, то точность потеряна, а если больше, то запись результата расценивается как безграмотная
Если списывается показание прибора, то количество значащих цифр в числе должно соответствовать приборной точности. Результат косвенных измерений должен содержать столько значащих цифр, сколько даёт самый грубый прибор при базовых прямых измерениях. Так например, если ток через проводник измеряется с точностью до двух цифр (I =65 мА), а напряжение на нём – до четырёх (U =79,45 В), то сопротивление проводника должно вычисляться с округлением до двух значащих цифр:
R = 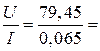 1,2 кОм=1,2·103 Ом.
1,2 кОм=1,2·103 Ом.
Примеры.
1) i =2,53 А – три значащие цифры; i =2,5 А – две (но i =2,50 А – уже три);
2) i =0,25 А=250 мА – две, но i =0,250 А=250 мА –три, так как здесь последний ноль является уже значащей цифрой, он показывается прибором;
3) i =5 мА=0,005 А=5·10−3 А – одна значащая цифра, но i =5,0·10−3 А=5,0 мА – две значащие цифры.
2. Расчёты. Все расчёты ведутся только в системе СИ. Хотя бы один контрольный расчёт каждой величины должен быть подробно представлен в рабочей тетради.
3. Графики. Общие требования к графикам следующие:
● графики представляются на миллиметровом или на клеточном листе прямо в рабочей тетради; их можно выполнять чернилами или хорошо отточенным мягким карандашом;
● график должен занимать бóльшую часть отведённого для него поля как по вертикали, так и по горизонтали; для этого надо правильно выбирать разметку осей;
● разметка осей должна быть равномерной и кратной целому числу клеток; на осях x и y указываются соответствующие величины и их размерности; на осях наносится по 3-5 опорных чисел, кратных 2, 5 или 10, но никак не 3, 6, 7 и т.д.; перегружать оси градуировочными числами не следует;
 ● экспериментальные результаты наносятся на график точками с какими-нибудь обводами, например, так:, и через них проводится плавная кривая (или прямая, смотря что ожидается), проходящая через все точки наилучшим образом (хотя бы в визуальном смысле);
● экспериментальные результаты наносятся на график точками с какими-нибудь обводами, например, так:, и через них проводится плавная кривая (или прямая, смотря что ожидается), проходящая через все точки наилучшим образом (хотя бы в визуальном смысле);
● для построения простых (монотонных) графиков обычно достаточно 6-8 экспериментальных точек, тогда как для сравнительно сложных кривых, типа амплитудно-частотной характеристики (АЧХ), нужно, минимум, 12-15 точек, чтобы ими были обозначены все детали кривой;
● график должен иметь название и, возможно, некоторые комментирующие сведения.
Пример 1. Пример 2.
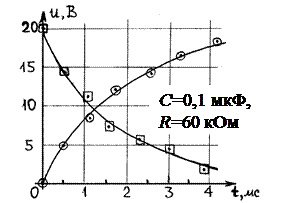
 Кривые заряда(
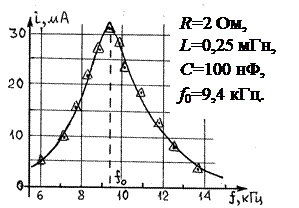
Кривые заряда( ) и разряда (() Амплитудно-частотная характерис-
) и разряда (() Амплитудно-частотная характерис-
конденсатора через резистор. тика последовательного контура.
 |  | ||
~~~~~~~~~~~~~~~~~~~~~~
4. ОБЩЕЕ ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ
По каждой работе в тетради должно быть записано следующее:
| № | Содержание записи | Примечания |
| Дата выполнения, название и цель работы. Схема установки или цепи. Основные рабочие формулы. Решение предложенных задач. Любая вспомогательная информация. | Дома, при подготовке к лабораторной работе. | |
| Результаты измерений (желательно, в виде таблиц) с правильной точностью. Примерный расчёт искомых величин. | Обязательно в лаборатории, перед подачей на подпись. | |
| Результаты расчётов с правильной точностью. Образец расчёта. Графики по форме. Комментарии в произвольной форме. | В лаборатории или дома. |
5. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
5.1. Понятие об измерении
Измерить физическую величину – значит сравнить её с аналогичной эталонной, принятой за единицу.
Методы измерений можно разделить на прямые и косвенные. В первом случае измеряемая величина определяется непосредственно по шкале прибора. Во втором – она определяется расчётом по результатам измерений других, связанных с нею величин. Так например, скорость автомобиля можно определить непосредственно по его спидометру, но можно и вычислить по результатам измерений пути s и времени t: υ = s/t. Сопротивление проводника можно измерить непосредственно омметром, но можно вычислить по результатам измерений тока и напряжения на нём: R = u/i.
5.2. Оценка точности одного прямого измерения
При определении многих физических величин прямым методом часто достаточно одного прямого измерения прибором. Так например, нет смысла при постоянных условиях многократно измерять выходное напряжение генератора, температуру в комнате, длину стержня. В этом случае результат измерения величины х записывается в виде:
х = х 0 ± Δ х пр,
где х 0 – измеряемое значение величины х, Δ х пр – абсолютная погрешность данного прибора.
Абсолютная погрешность прибора Δ х пр определяется его конструкцией и качеством, и превзойти её невозможно никаким методом измерений на нём. Прибор не может дать больше того, что заложено в его конструкции. Для более точных измерений надо взять прибор более высокого класса. Так например, если термометр имеет точность до 1° С, то, сколько бы мы им ни меряли, ни усредняли, точности 0,1° на нём не добиться. Линейкой с миллиметровыми делениями никак невозможно измерить длину стержня с точностью до 0,1 мм. Поэтому результаты измерений такими приборами следует записать, например, в виде:
Т = 24 ± 1°С, l = 250 ± 1 мм.
5.3. Оценка точности многократных прямых измерений
Часто возникают ситуации, когда при повторных измерениях величины х в одинаковых условиях получаются хоть и близкие, но заметно отличающиеся значения х 1, х 2, … хn. В этом случае говорят, что величина х имеет случайный, или статистический характер. Случайной величиной может быть, например, время падения шарика с крыши, измеряемое секундомером с точностью до 0,01 с. Или длина комнаты, измеряемая короткой линейкой с точностью до 1 мм.
Если измеряемая величина х имеет случайный характер, то наилучшей её оценкой является среднее арифметическое из проделанных п измерений:
х = < х > = 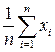 .
.
Погрешность Δ х сл, которая называется случайной, оценивается по формуле:
Δ х сл = 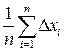 ,
,
где Δ хi = │ хi –< x >│ − погрешность отдельного измерения.
При наличии и систематической (приборной) погрешности Δ х пр (а она есть всегда), абсолютная погрешность измерений определяется по формуле:
Δ х = 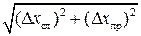 . (1)
. (1)
И тогда результат измерений величины х записывается в виде:
х = < х > ± Δ х. (2)
Из (1) видно, что если Δ х сл ≪ Δ х пр, то достаточно и одного измерения. Если же величина х имеет явно выраженный случайный характер, то в учебной лаборатории необходимо выполнить 4-5 её измерений.
Замечание. Случайную погрешность Δ х сл можно уменьшить, взяв более грубый прибор. Например, если длину комнаты измерять с точностью не до 1 мм, а до 10 см, то случайная погрешность может оказаться вообще нулевой. Но тогда в ещё большей степени возрастёт величина Δ х пр, так что общая абсолютная погрешность (1) увеличится.
Определение. Безразмерная величина
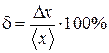 (3)
(3)
называется относительной погрешностью измерений.
Результат измерений величины х часто удобно записывать в виде:
х = < х > ± δ%.
Однако для некоторых величин, например, - температуры, форма записи (3) неприемлема, а только (2).
5.4. Оценка точности косвенных измерений
Пусть искомая величина f является функцией от измеряемых величин х и у, т. е. f = f (х, у). Тогда наилучшее значение f будет таким:
f = < f > = f (< х >, < у >).
В качестве абсолютной погрешности косвенного определения величины f при этом можно принять величину Δ f, вычисляемую по правилам дифференцирования:
Δ f = 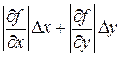 ,
,
где Δ х и Δ у определяются по формуле (1).
Относительная погрешность определения расчётной величины f
δ f = 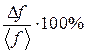 /
/
Пример 1. Пусть 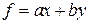 . Тогда
. Тогда 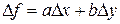 ,
, 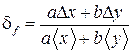 .
.
Пример 2. Пусть 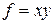 , тогда
, тогда 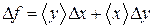 ,
, 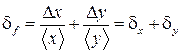 .
.
Пример 3. Пусть 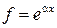 . Тогда
. Тогда 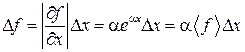 ,
, 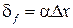 .
.
5.5. Обработка экспериментальных результатов
методом наименьших квадратов
Есть много способов оценки среднего значения результатов измерений. Однако при небольших разбросах экспериментальных величин и разного рода их средние будут отличаться друг от друга несильно. Пусть, например, есть два числа: х 1 = 9, х 2 = 10. Тогда их среднее арифметическое
<х >ар= 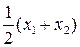 =9,50,
=9,50,
 2015-05-30
2015-05-30 424
424








