Решение.
Задача 1.
Если A 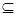 B, то
B, то 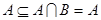
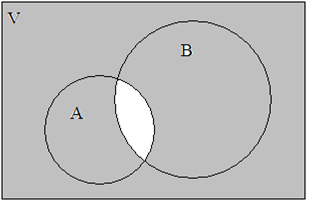
С помощью кругов Эйлера изображается так:
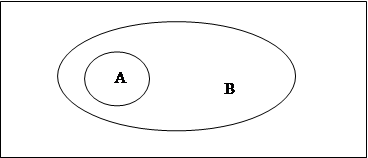
Пример.
А={ 2, 4}.
В={-3,-1, 2, 4}.
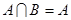 ={ 2, 4}.
={ 2, 4}.
Задача 2. Упростить выражение.
(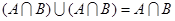
Задача 3. Является ли множество А={ 1,2,3} подмножеством множества В={ {1}, {2,3}}
Ответ. 
Множество А={ 1,2,3} не является подмножество множества В={ {1}, {2,3}}, т.к. в частности 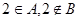 .
.
Задача 4.
Найти множество всех подмножеств множества С={ 3,5,8}
Решение. Булеан множества С равен:
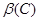 ={ { },{ 3},{ 5},{ 8},{ 3,5},{ 3,8},{ 5,8},{ 3,5,8}}
={ { },{ 3},{ 5},{ 8},{ 3,5},{ 3,8},{ 5,8},{ 3,5,8}}
Задача 5.
Даны числовые множества
А={ 26,18, 46,16}.
В={46,18,47, 26}.
С={ 26,48,50,51}
Найти: 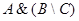
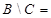 {46,18,47}.
{46,18,47}.
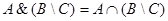 ={ 18, 46}.
={ 18, 46}.
Задача 6. Диаграмма Эйлера-Венна для множества 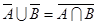 -штрих Шеффера
-штрих Шеффера
Задача 7.
Найти декартово произведение множеств А={ 5,1} и В={1,5,4}
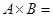 {(5,1),(5,5),(5,4), (1,1),(1,5),(1,4)}
{(5,1),(5,5),(5,4), (1,1),(1,5),(1,4)}
Задача 8.
Решение.
Определение. Бинарное отношение на множестве называют отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно
Пусть 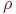 - отношение на множестве
- отношение на множестве 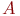 .Тогда
.Тогда
а) 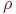 рефлексивно, если
рефлексивно, если 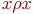 для
для  ;
;
б) 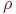 симметрично, если
симметрично, если  влечет
влечет 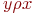 ;
;
в) 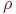 транзитивно, если
транзитивно, если  и
и 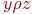 влечет
влечет 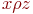 ;
;
Изобразим схематически отношение R.
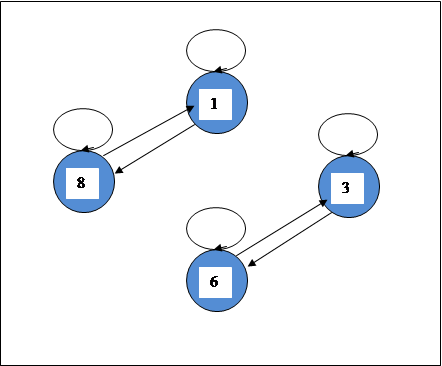 |
На диаграмме изображены 4 элемента множества М и 8 стрелок отношения R.
Определения рефлексивности, симметричности и транзитивности отношения заданного на множестве для диаграмм формулируются так:
a) отношение рефлексивно тогда и только тогда, когда для каждого узла на диаграмме существует стрелка-петля;
б) отношение симметрично тогда и только тогда, когда для каждой стрелки, соединяющей два узла, существует также стрелка, соединяющая два этих узла в обратном направлении.
в) отношение транзитивно тогда и только тогда, когда для каждой пары узлов 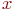 и
и 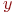 , связанных последовательностью стрелок от
, связанных последовательностью стрелок от 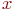 к
к 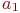 и от
и от 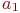 к
к 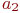 ..., от
..., от 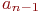 к
к 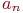 , от
, от 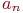 к
к 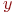 , существуют также стрелки от
, существуют также стрелки от 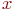 к
к 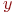 .
.
1) Каждый элемент на диаграмме имеет стрелку-петлю –это рефлекcивность R.
2) Отношение R симметрично так как для каждой стрелки, соединяющей два узла, существует также стрелка, соединяющая два этих узла в обратном направлении.
3) Отношение R транзитивно так для каждой пары узлов 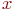 и
и 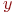 , связанных последовательностью стрелок от
, связанных последовательностью стрелок от 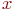 к
к 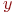 , существуют также стрелки от
, существуют также стрелки от 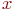 к
к 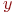 .
.
Ответ. Отношение R={(1,1),(3,3),(6,6), (8,8),(3,6),(6,3), (1,8) (8,1)} заданное на множестве М={1,3,6,8}является
отношением эквивалентности, так как оно рефлексивно, симметрично и транзитивно
 2015-05-22
2015-05-22 1923
1923







