Декартово (прямое) произведение множеств

ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ. СООТВЕТСТВИЯ, ФУНКЦИИ, ОТНОШЕНИЯ

ЦЕЛЬ ЛЕКЦИИ – изучение свойств декартова произведения множеств, и связанных с ним соответствий, функций и отношений.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Помимо рассмотренных в первой лекции традиционных операций над множествами существуют и другие действия с множествами, которые позволяют решать много задач, имеющих практическое применение. В частности, к таким действиям относится декартово (прямое) произведение множеств. Свое название декартово произведение получило оттого, что предложенное Декартом координатное представление точек плоскости, являлось исторически первым примером прямого произведения.

Декартово (прямое) произведение множеств

Декартово (прямое) произведение множеств Х и 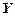– это множество, обозначаемое 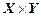, элементами которого являются упорядоченные пары 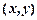, первая компонента которых принадлежит множеству Х, а вторая множеству .

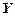Задается в виде

.

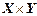
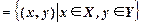Согласно определению элементами прямого произведения множеств являются упорядоченные пары, составленные из элементов исходных множеств. В этих парах первый элемент (компонента) всегда принадлежит первому множеству, а второй элемент (компонента) второму. Порядок множеств определяется исходной записью и, если 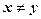, то 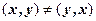, так как в упорядоченной паре 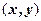компонента 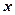имеет номер 1, а компонента 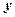– номер 2, но в упорядоченной паре 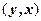: 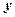– номер 1, а 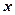– номер 2.

Множество 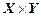содержит mn элементов, где m и n – количество элементов Х и 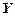соответственно.

Пример 2.1. Пусть A = {1, 2}, B = {1, 3, 4}. Тогда A × B = {(1, 1), (1, 3), (1, 4), (2, 1), (2, 3), (2, 4)}.

Геометрическое представление этого множества приведено на рис. 2.1, а.

Пример 2.2. Пусть A и B – отрезки вещественной оси. Прямое произведение изобразится заштрихованным прямоугольником, показанным на рис. 2.1, б.

Пример 2.3. Найти декартово произведение множеств 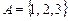и .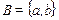

Решение. A × B .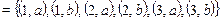

Порядок перечисления элементов безразличен, важен только порядок элементов в паре (упорядоченная пара).

B × A .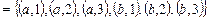

Из приведенных примеров видно, что свойства прямого произведения отличаются от свойств обычного произведения в арифметическом смысле. В частности, прямое произведение изменяется при изменении порядка сомножителей, то есть 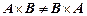, следовательно, декартово произведение не коммутативно. При этом он не только не коммутативно, но и не ассоциативно, но дистрибутивно относительно объединения, пересечения и симметрической разности множеств

;

;

.

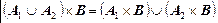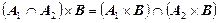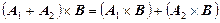Прямое произведение множеств – операция многоместная

.

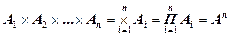В результате получаются множества, состоящие из упорядоченной последовательности вида

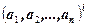, где ; ;…; .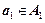

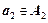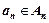Такие последовательности называются кортежами или векторами.

Кортеж длины 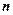– конечная последовательность элементов 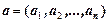, в которой каждый элемент занимает определенное место в соответствии с записью исходных множеств 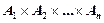декартова произведения.

Сами элементы при этом называются компонентами (координатами) кортежа, которые нумеруются слева направо (первая компонента, вторая компонента и т.д.).

Примеры кортежей: множество людей, стоящих в очереди, числа, выражающие координаты точки на плоскости и т.п. Во всех этих множествах место каждого элемента является вполне определенным и не может быть произвольно изменено.

Число элементов кортежа (вектора) называется его длиной. Кортеж из двух компонентов называется парой, из трех – тройкой и т.д. Для задания n- компонентного кортежа используются круглые скобки, в которых через запятую перечисляются компоненты кортежа, например a = (a ₁, a ₂,..., a_n).

Основные отличия понятий кортежа (вектора) и множества заключаются в следующем:

1) в множестве порядок элементов не играет роли, а кортежи, отличающиеся порядком элементов, различны, даже в случае, когда они имеют одинаковый состав;

2) в множестве все элементы различны, а в кортеже координаты могут повторяться.

Таким образом, в отличии от обычного множества в кортеже (векторе) могут быть одинаковые компоненты: два одинаковых слова в фразе, одинаковые численные значения координат точки на плоскости и т.п.

Два кортежа (вектора) считаются равными, если их длина одинакова и соответствующие компоненты равны между собой. То есть, если (a ₁, a ₂,..., a_n) = (b ₁, b ₂,..., b_n), то a_i = b_i для всех i = 1, 2,..., n.

Таким образом, декартово произведение позволяет получать вектора любых размерностей. Эта операция отличается от операций объединения и пересечения тем, что в результате перемножения прямым способом получаются объекты, содержащие элементы, отличающиеся по своей природе от элементов исходных множеств.

Если перемножить n раз одно и то же множество, то получится множество 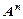, называемое степенью множества

.

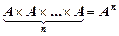Степенью декартового произведения называется число множеств n, входящих в это декартово произведение.