
1) Подмножество: 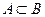
Если может быть А = В, то пишут 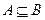 .
.

2) Объединение множеств: 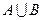
Определение 6. Объединением множеств А и В называется множество 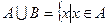 или
или 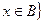 .
.
Свойства объединения: а) 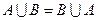 , б)
, б) 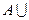
 = А, в)
= А, в) 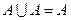 , г) если
, г) если 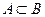 , то
, то 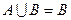

3) Пересечение множеств: 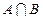
Определение 7. Пересечением множеств А и В называется множество 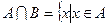 и
и 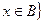 .
.
Свойства пересечения: а) 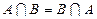 , б)
, б) 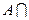
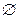 =
= 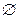 , в)
, в) 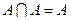 , г) если
, г) если 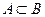 , то
, то 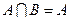
Определение 8. Два множества называются непересекающимися, если 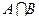 =
= 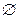 .
.

 4) Разность множеств:
4) Разность множеств: 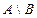
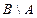
Определение 9. Разностью множеств А и В называется множество М,которое содержит всеэлементы А, не входящие в В: 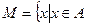 и
и 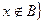 .
.
Свойства разности: а) 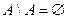 , б)
, б) 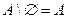 .
.
 5) Симметрическая разность: А
5) Симметрическая разность: А  В
В
Определение 10. Симметрической разностью множеств А и В называется множество А  В
В 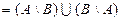
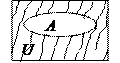 6) Если все построение происходит на некотором фиксированном множестве U, то U называют универсальным множеством. Его графически удобно изображать в виде множества точек прямоугольника.
6) Если все построение происходит на некотором фиксированном множестве U, то U называют универсальным множеством. Его графически удобно изображать в виде множества точек прямоугольника.
Дополнение множества А: 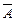
Определение 11. Если 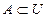 , то множество элементов
, то множество элементов 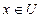 , но
, но 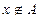 называется дополнением множества А относительно множества U и обозначается
называется дополнением множества А относительно множества U и обозначается 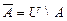 , т.е дополнением множества А называется разность
, т.е дополнением множества А называется разность 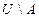 .
.
 2015-05-22
2015-05-22 665
665








